ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Tangente(s) au cercle   » tangente commune à deux cercles : méthode élémentaire | usage des homothéties   »  cas de deux cercles tangents | tangente et angle inscrit | exercices cercles tangents

La tangente (du latin tangere = toucher) en un point d'un cercle est une droite qui « touche »  le cercle sans le « couper ». Une sécante (du latin secare = couper) est une droite rencontrant (coupant) le cercle en deux points.

On considère un cercle (c) de centre O et une droite (d); on appelle H le pied de la perpendiculaire à (d) qui passe par O.

• Si l'on "glisse" (d) vers (c) jusqu'à toucher le cercle sans le couper, on dit que (d) est tangente en H au cercle et que H est le point de contact de la tangente.

•  En continuant de "glisser", (d) coupe le cercle (c) en deux points H1 et H2; on dit qu'elle est sécante au cercle en ces deux points.

On retiendra :    

1. la tangente en un point d'un cercle est la perpendiculaire au rayon aboutissant au point de contact.

2. D'un point M extérieur à un cercle on peut mener deux tangentes à ce cercle; elles touchent le cercle en A et B
   et on a MA = MB.     » la droite (OM) est un axe de symétrie de la figure.

Si votre navigateur accepte les applets Java (» extension CheerpJ) :
Placez le curseur sur (d) et faites glisser la droite. Depuis le point M que vous pouvez déplacer, on peut tracer deux tangentes à (c)

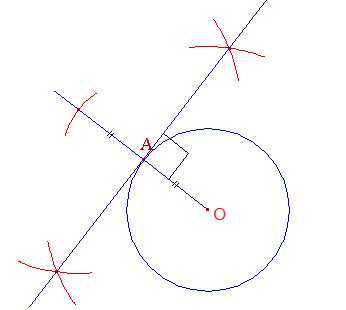
• Je trace une demi-droite d'origine O.

• Avec A comme centre, je trace un arc de cercle de rayon OA pour obtenir un segment dont A est le milieu.

• Avec la règle et le compas, je trace la médiatrice de ce segment : c'est la tangente cherchée.

• Avec la règle et le compas, je trace la médiatrice de [AO] : cela me donne le milieu de [AO].

• Je trace le cercle de diamètre [AO]; il coupe le cercle en deux points T1 et T2.

• Je trace une droite passant par A et par un de ces deux points : c'est une des deux tangentes au cercle passant par A.

On remarquera que par symétrie axiale, d'axe (AO), les segment [AT1] et [AT2] ont même mesure :

Les segments tangents issus d'un point extérieur à un cercle ont même mesure

Cercles tangents intérieurement :   

Considérons un cercle (c) de centre O, de rayon R, et sa tangente (T) en un point K. On sait que cette tangente est perpendiculaire au rayon [OK]. Traçons intérieurement au cercle (c) un cercle (c') de rayon r < R admettant la même tangente : on a [O'K] perpendiculaire à (T) et les centres O et O' sont alignés avec K. En conclusion :

Lorsque les cercles sont tangents intérieurement (le cercle de rayon r < R est à l'intérieur du cercle de rayon R), l'unique tangente commune aux deux cercles est la perpendiculaire au point de contact à la droite des centres.

Cercles tangents extérieurement ou non... : 

 ➔  Le cas de cercles tangents extérieurement est plus subtil et les constructions proposées ci-dessous s'appliquent sans modification à la construction des tangentes extérieures et intérieures à deux cercles de rayons distincts, tangents ou non :

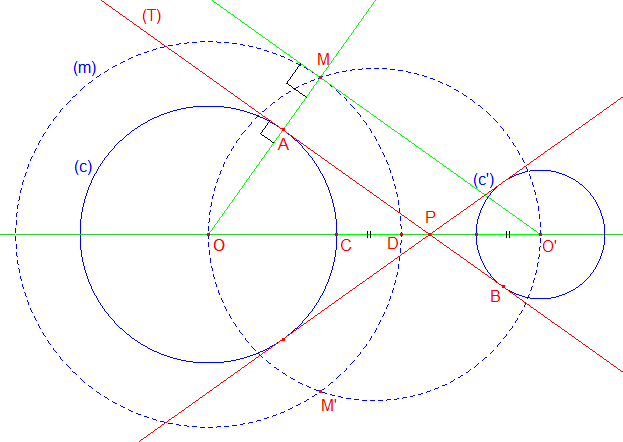
a) Tangentes extérieures :    

Considérons deux cercles (c) et (c') de centres respectifs O et O', de rayon R et r. Si R = r, la construction ne pose pas vraiment problème. Supposons donc les rayons distincts : R > r.

• Traçons le cercle (m) de centre O de rayon R - r (sans mesurer, reporter r = CD avec le compas);

• Le cercle de diamètre OO' coupe (m) en M et M'. Selon la construction de la tangente à un cercle issue d'un point extérieur à un cercle, [O'M) est une des tangentes à (m) issues de O';

• La demi-droite [OA) coupe (c) en A;

• Traçons la perpendiculaire (T) en A à [OA).

 ➔  Nous allons montrer que (T) est une des deux tangentes communes à (c) et (c'). La seconde s'obtient au moyen du point M' ou par symétrie axiale d'axe (OO'). Par raison de symétrie les tangentes se coupent en un point P de la droite des centres.

Preuve : par construction, (T) est tangente en A au cercle (c) car [OA], rayon de (c), est perpendiculaire à (T). On a donc (T) // (MO'). Traçons la parallèle à (MA) issue de O'; elle coupe (T) en B. Le quadrilatère ABO'M est un parallélogramme ayant un angle droit : c'est un rectangle. Par conséquent O'B = AM = r et (O'B) est perpendiculaire à (T) : c'est dire (T) est également tangente à (c') au point B.

Lorsque les cercles sont tangents extérieurement, la construction est en tout point semblable et les cercles admettent 3 tangentes communes :

b) Tangentes intérieures :    

L'étude est très proche de la précédente. Les cercles sont supposés non sécants. Le cercle auxiliaire (m) est ici de rayon R + r et la figure ci-dessous fera aisément comprendre la construction des deux tangentes intérieures (en rouge) :

Tangentes communes à deux cercles (cas général, par usage des homothéties, équations) : »

∗∗∗  
Un cercle, trois tangentes et un triangle... , Construction d'un cercle tangent à deux demi-droites
Cercles tangents et angle inscrit , Trois cercles tangents deux à deux : #1 et 2 , #3