
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
» Médiatrice d'un segment | Symétrie axiale | Bissectrice | Cercle circonscrit | Cercle inscrit | Cercles exinscrits | Symétrie centrale |
La notion de symétrie, au sens des transformations, est récente : milieu du 19è siècle avec le renouveau de la géométrie. Mais le concept est très ancien et était déjà cher aux architectes et mathématiciens de l'antiquité. Le terme provient du grec sun = avec et metron = mesure pour signifier respectant la mesure et impliquant chez les Grecs l'idée d'harmonie.
Thalès est sans doute le premier mathématicien à établir des théorèmes (du grec theorema = ce que l'on observe, ce qui est avéré) en se fondant sur le principe intuitif de symétrie : un diamètre partage un cercle en deux demi-cercles superposables. C'est la première symétrie axiale constatée de l'histoire des mathématiques.
Les toutes premières propositions d'Euclide s'attachent à mettre en place les éléments de symétrie dans les triangles isocèles (du grec iso = égal et skelos = jambe) et équilatéraux. La bissectrice d'un angle se présente implicitement comme un axe de symétrie de l'angle.
Platon ne peut imaginer l'harmonie du Monde qu'au travers de l'existence des cinq célèbres polyèdres réguliers convexes présentant le maximum de symétries dans le plan et l'espace. Euclide les étudiera dans son livre XIII.
Les sculpteurs et architectes grecs et romains, comme Vitruve, voient dans la symétrie (symmetria) non seulement l'équilibre et l'harmonie du Monde mais aussi la solidité, la force, à l'image du corps humain. A la Renaissance, Leonard de Vinci s'inspirera de ces convictions gréco-romaines.
On a pu constater de nos jours la présence systématique de symétries dans les structures moléculaires et l'étude des cristaux, entreprise au 19è siècle conduit à des situations complexes de symétries par rapport à des droites et des plans.
![]()
Mais
un excès de symétrie n'est pas toujours heureux et on peut préférer une symétrie
moins évidente, en quelque sorte brouillée,
comme cette rose dont la beauté,
fruit d'un hasard ordonné, est plus émouvante !

➔ Les concepts géométrique et algébrique de symétrie et de groupe se rencontrent également aujourd'hui en mécanique quantique et tend à expliquer la stabilité de la structure atomique de la matière depuis le Big-bang :
particule et antiparticule : électrons et positons;
quark et anti-quark;
opposition des pôles magnétiques;
principe d'action/réaction;
|
Médiatrice d'un segment : |
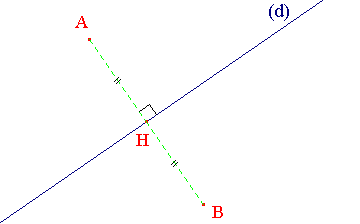
Dans un plan, on appelle médiatrice d'un segment la droite perpendiculaire à ce segment en son milieu (c'est à dire passant par son milieu noté H ci-dessous).
♦ Propriété 1 :
Tout point situé sur la médiatrice d'un segment est équidistant (à égale distance) de ses extrémités
Preuve : par construction, les triangles MAH et MBH, rectangles en H, sont isométriques (MH est commun et AH = BH). Donc MA = MB.

![]()
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Vous pouvez
déplacer la droite (d) et les points A et M
♦ Propriété 2 :
Si M est situé la médiatrice du segment [AB], alors MA = MB
♦ Propriété 3 (réciproque) :
Étant donné un segment [AB] et un point M, si MA = MB, alors M est situé sur la médiatrice de [AB]
♦ Construction de la médiatrice d'un segment :
En utilisant la propriété caractéristique ci-dessus :
Tracer le cercle de centre A passant par B;
Tracer le cercle de centre B passant par A;
Les deux cercles se coupent M et N;
La droite (MN) est la médiatrice de [AB]; elle coupe [AB] en son milieu J.
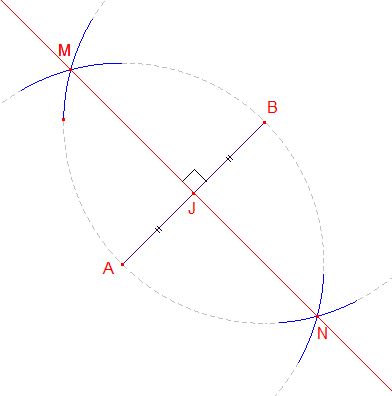
r1/ Afin de ne pas alourdir la figure, on se contente généralement de tracer des arcs de cercle de "part et d'autre" du segment [AB] comme illustré à droite.
r2/ Les arcs de cercle peuvent ne pas passer par A et B mais ils doivent être de même rayon (de mesure supérieure à AB/2). Le quadrilatère MANB est un losange dont les diagonales sont perpendiculaires et se coupent en leur milieu : la droite (MN) est la médiatrice du segment [AB] et la droite (AB) est la médiatrice du segment [MN].
Formule des sinus : »
|
La symétrie axiale : |
Dans le plan ou l'espace, on appelle symétrie d'axe (d) ou symétrie par rapport à la droite (d), la transformation qui à tout point A associe le point B tel que (d) soit médiatrice de [AB] si A∉(d) et A lui-même sinon.

Le château de Breteuil (début du
17è), (Yvelines, France) .
Si on omet le cas de quelques cheminées, on
peut voir là une symétrie par rapport à un plan vertical.
On dit que B est le symétrique (ou l'image) de A dans la symétrie d'axe (d). Dans une telle symétrie axiale, les points de (d) sont invariants, en particulier H, milieu de [AB]. Dans le plan, on parle aussi de retournement. Dans l'espace, on remarquera qu'il s'agit d'une rotation d'angle π autour de (d), dans le plan perpendiculaire à (d) passant par H.
Tout comme la symétrie centrale, une symétrie axiale est une isométrie. En particulier, elle conserve :
les distances;
l'alignement : les images de points alignés sont alignées;
les milieux : le symétrique du milieu d'un segment est le milieu du symétrique de ce segment;
le parallélisme : les symétriques
de deux droites parallèles sont parallèles;
mais une droite n'est en général pas transformée en une droite parallèle; les
cas particuliers sont les droites parallèles ou perpendiculaires à l'axe.
les angles
géométriques sont conservés (un angle et son symétrique ont même mesure).
Dans le plan, les angles orientés sont changés en leurs opposés mais
non pas dans l'espace puisqu'il s'agit d'une rotation d'angle π autour de (d).
➔ Dans le plan, la construction de B se fait au seul compas en utilisant le fait que les diagonales d'un losange sont perpendiculaires et se coupent en leur milieu :
Un cercle de centre A coupe la droite (d) en E et F;
Les cercles de centres E et F passant par A se recoupent au point B cherché car AEBF est un losange.

Noter que la construction de la droite perpendiculaire à (d) passant par A peut bénéficier de la même méthode : les cercles de centres E et F sont de même rayon mais ne passent pas nécessairement par A.
➔ Dans l'espace, il existe une infinité de droites perpendiculaires à un segment [AB] et passant par son milieu : elles constituent le plan médiateur de [AB]. Dans un tel cas, le point B est l'image de A dans la symétrie par rapport au plan coloré en jaune. On parle également de réflexion pour désigner cette application affine.
Isométries du plan et de l'espace : »


Un magnifique exemple de symétrie : Le château de
Cheverny (Loir et Cher, val de Loire), dont Hergé s'inspira
pour le château de Moulinsart du célèbre capitaine Haddock, en ne conservant que
la partie
centrale et les deux ailes symétriques qui la bordent.
∗∗∗
Médiatrice et cercles
(6ème/5ème) | Symétries
axiales et somme des angles d'un
triangle (6ème)
Une figure géométrique (F) est dite posséder un axe de symétrie (d) si elle est globalement invariante dans la symétrie d'axe (d).
Tout diamètre d'un cercle C est un axe de symétrie de ce cercle; les points s'échangent de part et d'autre du diamètre mais, globalement, la figure est inchangée : on obtient le même cercle et, dans la symétrie s d'axe (d), on est en droit d'écrire s(C) = C. Et pourtant, seuls les points I et J de C sont invariants. s(A) = A' et s(A') = A; s(B) =B' et s(B') = B; s(I) = I, s(J) = J. Une symétrie est une involution : c'est une bijection qui coïncide avec sa réciproque : s = s-1.
➔ Noter aussi que la bissectrice d'un angle (voir ci-après) est l'axe de symétrie de l'angle.
Axe de symétrie d'une courbe y = f(x) : » Symétrie dans les structures cristallines : »
∗∗∗
Bissectrice, symétrie
axiale & Losange (apprendre à démontrer)
| Exemple de symétrique d'une figure par rapport à une droite : le F majuscule : |

![]()
Si votre navigateur accepte les applets Java
(»
extension CheerpJ![]() )
:
)
:
Vous pouvez
déplacer les points A, B et C
|
∗∗∗ |
| Programme de construction apprendre à construire, mesures et symétrie axiale |
| Construction d'un point apprendre à construire (équidistance) |
| Un exercice de construction droite de Steiner |
| Trapèze isocèle construction & étude de ses propriétés |
| Médiatrice et mesures d'angles apprendre à construire, apprendre à démontrer |
|
Un problème axial apprendre à construire (bissectrice & symétrie axiale) |
| Adduction minimale symétrie axiale (4è) ou fonction irrationnelle (1ère) |
| Composée de deux symétries axiales TD niveau 6ème/5ème |
| Symétrie centrale et symétrie axiale TD niveau 5ème/4ème |
| Triangle mobile droite des milieux, angles inscrits, parallèles |
| Un faux problème symétrie axiale |

| Cercle circonscrit à un triangle, lien avec l'orthocentre : |
Considérons un triangle ABC et les médiatrices des côtés [AB] et [AC]. Elles se coupent en un point O vérifiant OA = OB d'une part et OA = OC d'autre part. On en déduit OB = OC : le point O est donc également situé sur la médiatrice de [BC] :
Dans un triangle, les médiatrices des côtés sont concourantes
en un point situé à égale distance des trois sommets :
c'est le centre du
cercle circonscrit (du latin
circum = autour et scriptum
= tracé, écrit).

Remarques :
1. Une ligne plane brisée et fermée peut admettre un cercle circonscrit : tous ses sommets doivent appartenir à un même cercle. On dit que ces points sont cocycliques. Tel est le cas du rectangle et du carré et plus généralement de tous les polygones réguliers.
2. Dans le cas du triangle rectangle s'interprétant comme un demi-rectangle, le centre du cercle circonscrit est situé au milieu de l'hypoténuse qui est ainsi un diamètre du cercle :
Tout triangle rectangle est inscriptible dans un demi-cercle dont un diamètre est son hypoténuse
3. Si un triangle admet un angle obtus (> 90°), alors le centre du cercle circonscrit se situe à l'extérieur du triangle. Le triangle rectangle apparaissant comme le cas limite.
![]()
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() )
:
)
:
Vous pouvez visionner ces deux derniers
résultat. Pour ce faire,
déplacez les points A, B et C
➔ Rappelons ici une formule pratique liant les mesures des côtés d'un triangle ABC, a = BC, b = CA, c = AB, à celles de ses angles et du rayon R de son cercle circonscrit :

♦ Un résultat intéressant concernant l'orthocentre d'un triangle :
On a tracé ci-dessous un triangle ABC et ses trois hauteurs sécantes en H, orthocentre du triangle.
Dans un triangle, les symétriques de l'orthocentre par rapport à chacun des côtés est situé sur le cercle circonscrit.

Équation du cercle circonscrit : » Cercle des neuf points : »
| Bissectrice d'un angle : |
Étant donné un angle ^xOy de sommet O, de côtés [Ox) et [Oy), on appelle bissectrice de cet angle la demi-droite [Oz) partageant cet angle en deux angles superposables (de même mesure) ^xOz et ^yOz :

![]()
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Vous pouvez réduire/agrandir l'angle (en agissant sur les côtés) et déplacer M
♦ La bissectrice d'un angle est l'axe de symétrie de cet angle et, à l'instar de la médiatrice d'un segment : tout point situé sur la bissectrice d'un angle est équidistant (situé à égale distance) de ses côtés :
Si M est situé sur (Oz), bissectrice de ^xOy, alors MH = MK
Inversement :
Étant donné un segment ^xOy et un point M, si MH = MK, alors M est situé sur la bissectrice de ^xOy.
|
∗∗∗ |
| Bissectrice et parallèles construction de la bissectrice d'un angle |
|
Parallélogramme & bissectrices #1 géométrie élémentaire |
|
Parallélogramme & bissectrices #2 prolongement |
|
Bissectrice, symétrie axiale & Losange apprendre à démontrer |
| Barrettes mobiles... problème de construction |
|
Cercle inscrit dans un triangle : » Cercle inscrit dans une figure plane |
Considérons maintenant un triangle ABC et les bissectrices des angles ^ABC et ^BAC : ce sont les axes de symétrie de ces angles. Par suite, le point O en lequel elles se coupent est situé à égale distance des côtés [BA] et [BC] d'une part et [AB] et [AC] d'autre part. On en déduit que O est à égale distance de [CB] et [CA] : le point O est donc également situé sur la bissectrice de ^ACB.
En notant H, K et L les projections orthogonales de O sur les trois côtés, on a :
OH = OK = OL, (OH) ⊥ (BC), (OK) ⊥ (AB), (OL) ⊥ (AC)
C'est dire que le cercle de centre O de rayon OH est tangent intérieurement aux trois côtés du triangle ABC (» tangente à un cercle).

Dans un triangle, les bissectrices des angles sont
concourantes en un point situé à égale distance des trois côtés :
c'est le
centre du cercle inscrit dans le triangle (du latin
inscribere = écrire dans)
tangent intérieurement aux trois côtés de ce triangle
![]()
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Vous pouvez réduire/agrandir le triangle en
déplaçant ses sommets
➔ Une ligne plane brisée et fermée peut admettre un cercle inscrit : pour cela, tous ses côtés doivent être tangents extérieurement à un même cercle. Tel est le cas du rectangle et du carré et plus généralement de tous les polygones réguliers.
∗∗∗
Calcul du rayon du cercle inscrit
dans un triangle , Problèmes d'Apollonius ,
Lemme de Bricard
| Cercles exinscrits d'un triangle : |
Considérons un triangle ABC et les bissectrices des angles extérieurs ^ABx et ^BAy : ce sont les axes de symétrie de ces angles. Par suite, le point O en lequel elles se coupent est situé à égale distance de [Bx) et [BA] d'une part et [Ay) et [AB] d'autre part. On en déduit que O est à égale distance de [Cx) et [Cy) : le point O est donc également situé sur la bissectrice de ^ACB :
Dans un triangle, les bissectrices de deux angles extérieurs et d'un angle intérieur sont concourantes en un point situé à égale distance des trois côtés * : c'est le centre d'un cercle dit exinscrit (du latin ex = à l'extérieur de et scribere = tracer, écrire dans) tangent aux trois côtés *.
* Il y a ainsi trois cercles exinscrits dans un triangle que l'on précise par la locution exinscrit dans l'angle ^A, ^B ou ^C. Ci-dessus, lorsqu'on parle des trois cotés, il s'agit suivant le contexte d'un segment, comme [AB] ci-dessous, et des deux demi-droites prolongeant les deux autres deux côtés, comme (Cx) et (Cy) ci-dessous.

On remarquera que
les bissectrices intérieures et extérieures sont perpendiculaires,
ce qui
s'explique de façon très naturelle...
Calcul du rayon des cercles exinscrits en fonction des côtés et de l'aire du triangle : »
![]()
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Vous pouvez réduire/agrandir le triangle en
déplaçant ses sommets
» Feurerbach , Apollonius

Château de Chambord (1-è siècle), Loir et Cher, France
»
http://www.chambord.org/index.htm
Belle symétrie ? oui et non : il y a quelques erreurs sans
doute volontaires...
∗∗∗
Un petit
problème axial
apprendre à construire (bissectrice, symétrie
axiale, cercle exinscrit)
Construire un cercle tangent à 3 droites
(problème d'Apollonius)