
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» cas général : développante d'une courbe , engrenage |
 |
Prélude : Faites l'expérience suivante :
Enroulez un fil autour d'une bobine (objet cylindrique), les spires restant proches les unes des autres. Ci-contre : fil de lin et boîtier de pellicule 24×36; la base du boîtier a été décrite au stylo rouge.
Fixez un crayon bien taillé à l'extrémité (faites en sorte que l'attache soit à la même hauteur que l'enroulement);
Placez l'ensemble sur une feuille de papier et commencez à tracer en déroulant la ficelle tout en tendant celle-ci (au départ la mine touche le bord de la bobine).
Vous devez obtenir une sorte de spirale comme sur la photo ci-contre.
Nom de la courbe : développante de cercle.
Etymologie : du verbe développer.

Définitions possibles :
Outre celle, plus générale, donnée par Huygens dans sa théorie des développantes, on peut donner la définition suivante correspondant à l'expérience ci-dessus :
Considérons un cercle (c) et une demi-droite (d) tangente à (c) en un point initial To. Lorsque le point de tangence T, initialement en To, décrit (c), soit M le point de (d) tel que la distance TM égale la mesure de l'arc TTo du cercle. Le point M décrit une trajectoire appelée développante du cercle (c).

Equation :
Dans un repère orthonormé direct (Ox,Oy) dont l'origine est au centre O du cercle de rayon r, (Ox) étant porté par OTo, notons M(x,y) le point de la courbe étudiée. L'équation paramétrique s'obtient aisément par projection de M sur les axes en remarquant que les coordonnées de T sont xT = r.cos t, yT = r.sin t et que TM = r x t, d'où xM = OH = OK + KH (en mesure algébrique), soit :
x = r.cos t + rt.cos(t - π/2) = r.cos t + rt.sin t.
Procédant de même pour l'ordonnée de M, on en définitive :
x = r.cos t + rt.sin t , y = r.sint - rt.cos t
Génération :
La développante est générée ci-dessous au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Pour arrêter/relancer
double-cliquer dans la figure.
Vous pouvez agrandir/réduire
la "bobine" de centre O
![]() Le
logiciel CabriGéomètre n'accepte pas des angles supérieurs à 180°, ni des
longueurs d'arcs supérieurs à un tour de cercle (360°). C'est bien dommage. D'où
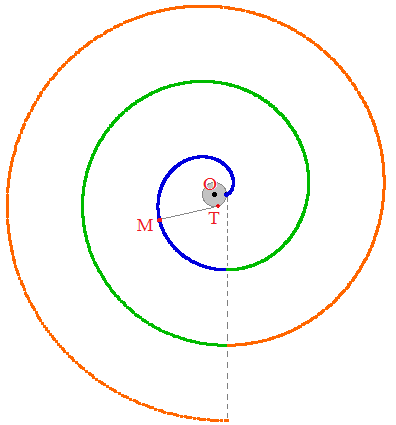
la triche ci-dessus : en bleu
le début de la développante correspondant à un tour;
en vert, on a rajouté
à la longueur du "fil" un tour complet et
en rouge,
deux tours, ce qui simule une développante sur 3 tours.
Le
logiciel CabriGéomètre n'accepte pas des angles supérieurs à 180°, ni des
longueurs d'arcs supérieurs à un tour de cercle (360°). C'est bien dommage. D'où
la triche ci-dessus : en bleu
le début de la développante correspondant à un tour;
en vert, on a rajouté
à la longueur du "fil" un tour complet et
en rouge,
deux tours, ce qui simule une développante sur 3 tours.
| Applications : |

En mécanique (au sens de l'étude théorique des mouvements : mécanique rationnelle, ainsi qualifiée par Newton) et au sens technologique : fabrication des engrenages. Le physicien et mathématicien J. W. Gibbs étudia la denture optimale des engrenages évitant les frictions.
Considérons tout d'abord un entraînement par courroie croisée d'une poulie p' (dite poulie menée) de centre O' par une poulie p de centre O (dite poulie menante) et intéressons-nous à un point M de la courroie située entre T1 et T2 (la droite T1T2 est tangente commune à p et p').
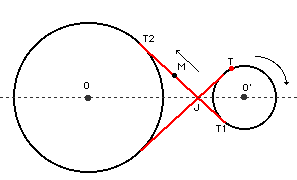
Soit T le point de p' qui coïncidait avec M en T1 à un instant donné. Relativement au point T, le point M décrit, entre T1 et T2 une développante de p' car la transmission (si la courroie ne glisse pas) permet d'affirmer l'égalité de T1M et de l'arc de cercle T1T. On a évidemment la même constatation en échangeant les rôles de p et p'.
Si l'on remplace les poulies par des roues dentées, ces considérations permettent de comprendre qu'on assurera un contact tangentiel optimal des dents (en J) lorsque la forme des dents (le profil) sera en forme de développante de cercle.
Ci-dessous : schéma d'un engrenage à denture droite fabriqué dans un cylindre de diamètre dt (diamètre de tête). Le diamètre de pied de l'engrenage est dp : c'est le diamètre du cylindre du cercle (C) sur lequel "reposent" les dents.
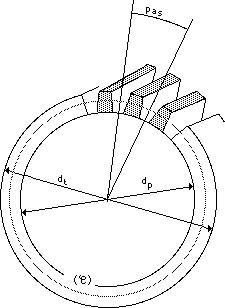
Le diamètre primitif de l'engrenage est le diamètre du cercle en pointillé sur le schéma (il passe par les demi-hauteurs des dents).
Le pas de l'engrenage est l'angle, exprimé en radians, mesurant l'écart angulaire entre deux dents consécutives.

➔
Pour en savoir plus et pour des schémas tant plus exacts qu'esthétiques... :Guide du dessinateur industriel, par A. Chevalier , Ed. Hachette Technique.
Calcul d'engrenages,
par Michel Delaboure :
1/
http://www.cours-et-exercices.com/2016/03/cours-des-engrenages.html
2/
http://www.cours-et-exercices.com/2016/04/calculs-dengrenages-presentation.html#Heading3
© Serge Mehl - www.chronomath.com