ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 Spirales à 2, 3, 4,
5 ou 6 centres
ou plus... |
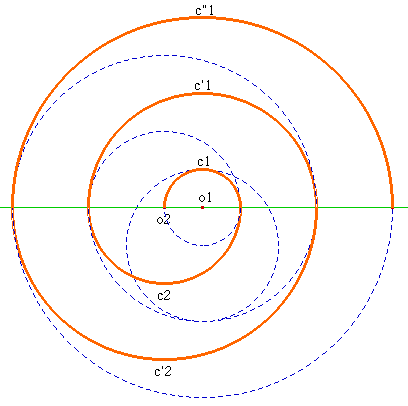
De telles spirales sont engendrées par des arcs de cercles dont le rayon croît indéfiniment de sorte que pour deux arcs consécutifs ci+1 et ci , les cercles (Ci+1) et (Ci) qui les supportent soient tangents intérieurement. Ci-dessous la spirale à deux centres o1 et o2 :
En dehors du cas de la spirale à 2 centres ci-dessus et ci-dessous, les centres sont les sommets de polygones réguliers et la mesure angulaire de l'arc est 2π/n (soit 360°/n) où n désigne le nombre de centres. Ces belles spirales se comprennent d'elles-mêmes par simple contemplation. Sont tracées ci-après les cas n = 2, 3, 4, 5 et 6.
Outre leur intérêt purement géométrique, ces spirales se retrouvent en architecture (volutes) ou dans les jardins à titre décoratif (haies basses, massifs fleuris) et sont plus simples à tracer que les spirales d'Archimède, de Bernoulli, de Fermat, ...
| 2 centres : arcs de 180° |
La distance entre les spires est constante; elle égale le diamètre 2r du 1er demi-cercle c1 de centre o1, de rayon r.
Le second tracé est le demi-cercle c2 de centre o2 de rayon r + r = 2r.
Le troisième tracé est le demi-cercle c'1 de centre o1 de rayon r + 2r = 3r.
Et ainsi de suite en alternant les deux centres o1 et o2.
| 3 centres : arcs de 120° |
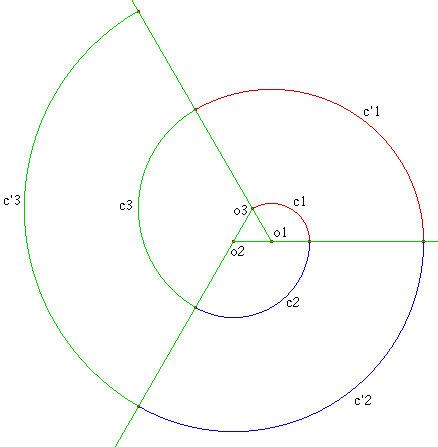
| 4 centres : arcs de 90°, principe de base de la volute ionique » Volute , Vitruve |
| 5 centres : arcs de 72° |
| 6 centres : arcs de 60° |
