ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 Promenade géodésique sur un cube... |
Un vilain bug (bestiole ou punaise, en anglais. » G.M. Hopper) veut se déplacer vers le point rouge de ce cube. Il utilisera le chemin le plus court (en quelque sorte, une géodésique : chemin le plus court sur une surface). Le côté du cube mesure 8 cm. Les cotes indiquées sont en cm et désignent les distances réelles.
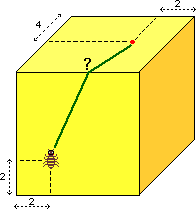
Pourriez-vous construire ce chemin sur le cube sans le déplier ?
➔ Cela revient à construire la position du point d'interrogation. Il n'est pas interdit de déplier mentalement le cube pour analyser la situation...
Si vous séchez après avoir bien cherché : ››››
| Solution : |
Le trajet du bug sera minimal si, en dépliant, on constate que M est un point du segment [AB].
Si H et K désignent respectivement les projections orthogonales de A et B sur l'arête contenant M, les angles ^HMA et ^KMB doivent être égaux; c'est dire que les triangles HMA et KMB sont homothétiques.
Afin de connaître la position de M, on applique la propriété de Thalès dans sa configuration "croisée" :
AH/BK = MH/MK
Revenons au cube et à sa face supérieure :
Eu égard aux mesures données, H et K sont à 2 cm des extrémités de l'arête contenant M.
AH = 6 et BK = 4. M est donc le point qui partage le segment [HK] dans le rapport 6/4 = 3/2.
Sur une oblique quelconque issue de H (figure de droite) :
on reporte au compas 5 mesures identiques;
on joint la dernière graduation D à K;
on trace la parallèle à (DK) issue de la troisième graduation T. Elle coupe [HK] au point M cherché.
