ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Apprendre à construire : constructions de triangles #7     TD  niveau 4è/3è       » #1 à 4 , #5 , #6 , #8 , #9 , #10        » Variante :  niveau 1ère/Ter

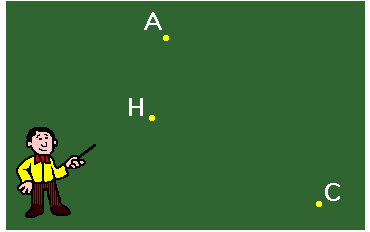
Construire le triangle ABC dont on a donné au préalable :

1. le sommet A;
2. le sommet C;
3. le point H, orthocentre du triangle : point de concours (point d'intersection) des trois hauteurs.

Analyse :    

On recherche le sommet B. Le côté [BC] est perpendiculaire à (AH) : le point B est situé sur la perpendiculaire à (AH) issue de C. La hauteur issue de B passe par H et est perpendiculaire à (AC) : connaissant H et (AC), on peut tracer cette hauteur. D'où la construction :

Construction :    

• Tracer [AC];

• Tracer la demi-droite [AH);

• Tracer la demi-droite [Cx) perpendiculaire à [AH) : elle portera le point B;

• Tracer la droite (Hy) perpendiculaire à [AC] : c'est la hauteur issue de B;

• (Hy) coupe [Cx) en B;

• Tracer [AB].

Synthèse :     

• On admet savoir ici que les hauteurs d'un triangle sont concourantes.

• Par construction, on a (CB) ⊥ (AH) et (AC) ⊥ (BH) : H est donc bien le point de concours des hauteurs (orthocentre).

• La figure obtenue répond donc aux conditions posées. La solution est unique car B est unique en tant qu'intersection de (Hy) et (Cx).

Toute construction doit être conduite par analyse et synthèse. L'analyse est le raisonnement aboutissant à la construction cherchée. Mais le processus d'analyse procède par implication : si ABC existe (on suppose la construction aboutie) alors on a nécessairement (forcément en langage élève) ceci ou cela, donc on va faire ceci ou cela.

La synthèse consiste à vérifier que ces conditions nécessaires aboutissant à la construction sont aussi suffisantes, c'est à dire que cette construction vérifie bien toutes les hypothèses de l'énoncé.