ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Selon Brigitte Sénéchal, dans son livre Géométrie classique et mathématiques modernes, le concours des hauteurs d'un triangle aurait été prouvé par Archimède selon la démarche ci-dessous. Les outils sont les propriétés des angles inscrits et l'inscriptibilité d'un triangle rectangle dans un demi-cercle  dont le diamètre est son hypoténuse.

• On considère un triangle ABC ayant ses trois angles aigus; 
  » on verra plus après le cas d'un angle obtus.

• On a tracé en vert les hauteurs issues de A et B; elles se coupent en H à l'intérieur du triangle ABC; on a noté A' et B' leurs pieds respectifs.

• En vert également, la droite (CH).

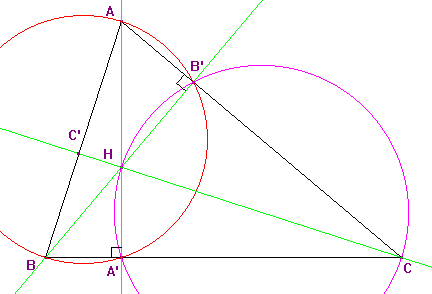
 ➔   L'objectif est de prouver que (CH) est perpendiculaire à (AB)

étape 1. Observe le quadrilatère A'HB'C; sa diagonale [HC] est  l'.......................... commune des deux triangles ...................... HA'C et ............ Par conséquent A' et B' appartiennent au ...................... de ..................... [HC].

étape 2. Observe maintenant le quadrilatère ABA'B'; pour les mêmes raisons que précédemment, on peut affirmer que A' et B' appartiennent au ............... de ........................ [AB].

étape 3. Étudions les triangles ABA' et C'BC; ils ont en commun l'angle ^B et dans ABA' l'angle ^A' est droit. Si nous montrons que les angles ^BAA' et ^BCC' ont même mesure alors ^BC'C sera droit. Ok ?.. alors, on continue :

étape 4. On a tracé en rouge le cercles (c1) de diamètre [.....]  et en rose le cercle (c2) de diamètre [.....]. Dans le cercle (c1), les angles ^BAA' et ^BB'A' ont même mesure car ils ....................... le même ...... BA'.

étape 5. Dans le cercle (c2), les angles ^HB'A' et ^HCA' ont même mesure car ils ....................... le même ...... HA'.

étape 6. Mais ^BB'A' n'est autre que ^HB'A'. Donc ^BAA' = ^HCA' et ce dernier angle n'est autre que ^BCC'.

CQFD : Ce Qu'il Fallait Démontrer...

Conclusion : les ................ du triangle ABC sont concourantes en H.

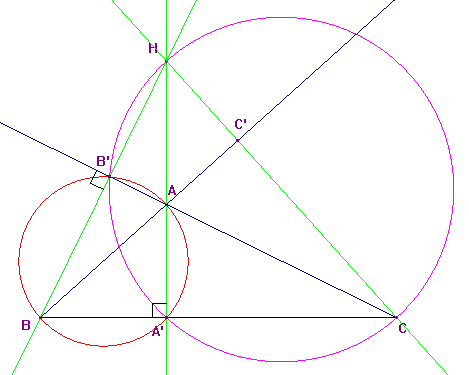
La même démarche s'applique ici. No more comment...