
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

| » Animation | Parabole cubique et fonction racine cubique |
Nom de la courbe : parabole
Etymologie : du grec parabolê, para = à côté et ballein = lancer, jeter. La parabole correspond à la trajectoire d'un projectile lancé et retombant à terre. Le terme est d'Apollonius de Perge.
Définitions possibles : la parabole est une des trois coniques (avec l'hyperbole, et l'ellipse dont le cercle peut être considéré comme un cas particulier) découvertes par les mathématiciens grecs en tant qu'intersection d'un cône par un plan (du grec kônos).
Étude générale des coniques : »
Approche élémentaire :
Nom de la fonction associée : trinôme du second degré.
Étymologie : du latin et du grec tri = trois et du grec onoma = nom (trois termes). Le mot clé est ici monôme contraction de mono = seul, un seul et onoma = nom. Nous avons aussi : binôme = deux termes, polynôme = plusieurs termes, du grec polus = plusieurs.
Équation cartésienne : y = ax2 + bx + c
Ensemble de définition : R
Périodique : non.
Forme réduite : monôme du second degré d'équation Y = aX2 par changement de variable X = x + b/(2a) et Y = y + b2/4a2 - c/a.
Fonction dérivée : 2ax + b ; fonction dérivée de la forme réduite : 2aX
Équation réduite y2 = 2px, paramètre de la parabole : »

➔ On dira de la parabole ci-dessus qu'elle présente sa convexité vers les ordonnées positives. La fonction x → x2/10 est convexe. A contrario, ci-dessous, la fonction x → -x2/10 est concave (» fonctions convexes).

∗∗∗
L'arc de courbe ci-dessous, présentant
un extremum en (1,-2), est-il celui d'une parabole ? Non, car si cela était la
symétrie par rapport à l'axe d'équation x = 1 devrait être plus manifeste... Par
exemple, la courbe semble passer par (2,-7) mais ne passe clairement pas par
(0,-7).
Il s'agit en fait d'une cubique d'équation y = x3 - 9x2 +
15x - 9

| Applications de la parabole : |
♦ Ponts suspendus : les câbles principaux des tabliers de ponts suspendus, comme ci-dessous, ont une forme parabolique. En fait, cette courbure parabolique est une approximation de chaînette.

Pont de Tancarville -Normandie,
France
La parabole soutenant le tablier principal fait subir des poussées horizontales exercées sur les piles. Ces forces sont équilibrées par les deux demi-paraboles fixées et réglées en conséquence sur les rives. D'où la nécessité, comme pour les barrages, d'une étude solide (dans tous les sens du terme) de la structure géologique des berges.

Pont de San Francisco, (Golden Gate bridge)
© TripAdvisor
 ♦
Viaducs et barrages :
à gauche, le barrage de Vouglans sur l'Ain et sa centrale hydro-électrique, construits par Électricité
de France (1964-1969). La voûte parabolique, à double courbure, s'élève à 103 m
de hauteur.
♦
Viaducs et barrages :
à gauche, le barrage de Vouglans sur l'Ain et sa centrale hydro-électrique, construits par Électricité
de France (1964-1969). La voûte parabolique, à double courbure, s'élève à 103 m
de hauteur.
On rencontre également des voûtes en arcs de cercles (anciennement et pour de petits barrages), en arcs d'ellipse ou encore en arc de spirale logarithmique (spirale de Bernoulli). Ces formes de courbes reportent la poussée des eaux sur les versants.
 à droite, le viaduc de Garabit
construit sur la Truyère (Cantal, France) par Gustave
Eiffel à partir des plans de l'ingénieur
Léon Boyer. L'arche est un arc de parabole chevauchant la rivière
et sa flèche, hauteur de l'arc à compter des piles, est de 57 m, la
distance entre piles étant de 165 m. Une telle structure parabolique assure une
grande résistance au fléchissement.
à droite, le viaduc de Garabit
construit sur la Truyère (Cantal, France) par Gustave
Eiffel à partir des plans de l'ingénieur
Léon Boyer. L'arche est un arc de parabole chevauchant la rivière
et sa flèche, hauteur de l'arc à compter des piles, est de 57 m, la
distance entre piles étant de 165 m. Une telle structure parabolique assure une
grande résistance au fléchissement.
Deux photos du viaduc de Garabit (attention haute résolution...) : »
♦ Mécanique, cinématique, : chute des corps (Galilée), balistique (mouvement des projectiles), équation horaire des mobiles soumis à une accélération uniforme.
♦ Astronomie : trajectoire apparente de certaines comètes n'appartenant pas au système solaire.
♦Dans l'espace (paraboloïde) : par rotation autour de son axe, une parabole engendre un paraboloïde de révolution (l'appellation est de Huygens) dont les propriétés émettrices et réceptrices résultent de la propriété focale de la parabole. On démontre facilement qu'un rayon lumineux (zM), figure ci-dessous, parallèle à l'axe du paraboloïde, se réfléchit au foyer F. Il y a donc accumulation de lumière en F. Inversement, une ampoule lumineuse placée au foyer F va projeter des rayons lumineux parallèles.

Cette définition se retrouve dès le 4ème siècle dans Pappus d'Alexandrie et, selon la légende, fut exploitée par Archimède pour repousser les navires ennemis à Syracuse en tentant de les brûler en renvoyant les rayons solaires au moyen de miroirs paraboliques.


Antennes & miroirs paraboliques : »
Ces propriétés expliquent les nombreux usages du paraboloïde en optique (phares), fours solaires, télescopes, transmission hertzienne (télévision par satellite, radioastronomie), radars = RAdio Detection And Ranging), mis au point par les anglais lors de la seconde guerre mondiale, etc.
» Newton
En savoir plus sur la parabole en tant que
conique :
»

Immeuble Poséidon, La
Grande Motte (Hérault, France)
| Fonction racine carrée : |
Pour tout x positif, le nombre positif y tel que y2 = x est la racine carrée de x (notée √x depuis Rudolff).
Les fonctions x → x2 et y → √x sont donc réciproques l'une de l'autre. Il suit que, dans un repère orthonormé, la représentation de la fonction y = √x est une parabole symétrique de la parabole d'équation y = x2 par rapport à la bissectrice principale du repère (aussi dite 1ère bissectrice) d'équation y = x.
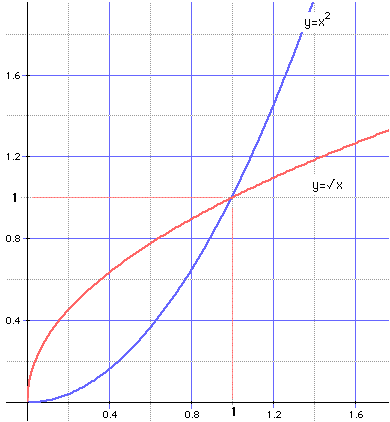
! la
symétrie axiale échangeant les deux courbes n'est effective qu'en repère
orthonormé !