
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
La méthode d'exhaustion repose sur le principe, souvent appelé axiome d'Archimède :
En soustrayant de la plus grande de deux grandeurs données plus de sa moitié, et du reste plus de sa moitié, et ainsi de suite, on obtiendra une grandeur moindre que la plus petite.
Par on obtiendra, on sous-entend là au bout d'un nombre fini de fois. Ce principe dichotomique évite un délicat passage à la limite, donc l'introduction du concept d'infiniment petit ou d'infiniment grand posant autant de problèmes mathématiques que philosophiques. Il faudra traverser les siècles pour aboutir à une mise en place satisfaisante du calcul "infinitésimal" : Leibniz, Pascal, d'Alembert, Euler, Bolzano, Cauchy, Weierstrass.
Tout comme pour le raisonnement par récurrence de Pascal, la méthode d'exhaustion nécessite une bonne intuition : celle du résultat !
Si R est ce dernier et A la grandeur étudiée (une aire, par exemple), on montre par deux raisonnements par l'absurde que l'on ne peut avoir ni A > R, ni A < R. Donc A = R.
Cette méthode exhaustive, puisqu'elle examine tous les cas, purement logique, n'est pas vraiment évidente à manipuler et montre tout le génie des géomètres grecs (Eudoxe, Archimède, Euclide,...) qui l'utilisèrent avec des moyens de calcul et d'écriture mathématiques pourtant lourds à "manipuler".
| Un exemple simple d'application de la méthode : |
Au titre Le Cercle, nous avons obtenu le périmètre et l'aire du cercle (on devrait plutôt dire "du disque") par une méthode modernisée de celle présente dans la Mesure du Cercle d'Archimède. Afin d'illustrer la méthode d'exhaustion, voici comment Archimède calcula l'aire du cercle :
Tout cercle est équivalent (au sens de même aire) à un triangle rectangle dont l'un des côtés de l'angle droit est égal au rayon du cercle, l'autre mesurant le périmètre du cercle.
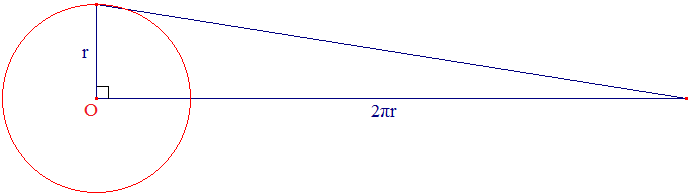
Sachant que le périmètre du cercle de rayon r est 2πr (» voyez Le Cercle), son aire sera alors ½ × r × 2πr = πr2 : c'est le résultat convoité. Soit donc r le rayon d'un cercle et L son périmètre.
a) Supposons que l'aire A du cercle soit supérieure à celle T du triangle :
Notons k = A - T. Inscrivons dans le cercle un carré ABCD, puis divisons en parties égales les arcs de cercle et répétons ces opérations de division jusqu'à obtenir, en application de l'axiome d'Archimède, A - P < k où P désigne l'aire des polygones réguliers inscrits obtenus par divisions successives des arcs.
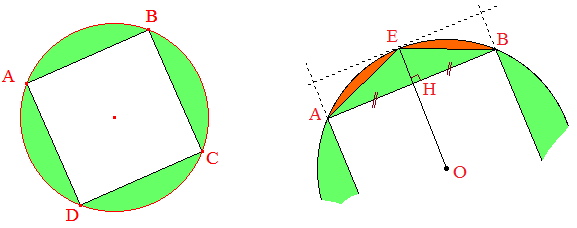
L'axiome d'Archimède s'applique en effet ici : d'une division à l'autre, la dichotomie utilisée supprime plus de la moitié de chaque "segment" de disque (en vert sur le dessin), la partie rouge montrant l'aire résultante. La symétrie marquée en pointillés montre que le "segment" de disque rouge a une aire inférieure à celle du triangle AEH.
On a donc A - P < A - T, soit : P > T. Pourtant, pour tout polygone régulier obtenu par division, OH est inférieur au rayon r du cercle et son périmètre p est inférieur à celui du cercle. Donc son aire P = OH × p/2 est plus petite que rL/2 = T. C'est dire : P < T. Ce qui est absurde.
l'aire A du cercle n'est donc pas supérieure à celle T du triangle
b) Supposons maintenant que l'aire A du cercle soit inférieure à celle T du triangle :
Inscrivons le dans un carré ABCD dont l'aire excède alors celle du cercle. On procède comme précédemment : posons k = T - A et traçons [OA] qui coupe le cercle en H. Traçons la tangente en H. Elle coupe le carré en K et L.
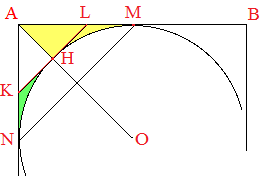
[KL] est le côté de l'octogone régulier circonscrit. L'aire jaune correspond à la moitié de l'excédent relatif à ce "coin" du carré. L'aire verte correspond à la moitié de l'excédent relatif à ce "coin" de l'octogone.
On a LM = LH. Le triangle AHL est rectangle isocèle et par suite AL > LM. L'aire verte délimitée par HLM est inférieure à l'aire du triangle HLM, laquelle est inférieure à l'aire du triangle AHL (puisque LM < AL). Par conséquent l'aire verte est inférieure à la moitié de l'aire jaune (décomposer : aire jaune = aire verte + aire triangle AHL).
Par application de l'axiome d'Archimède, par divisions successives, on obtiendra une suite de polygones réguliers circonscrits, d'aires notées P, et au bout d'un nombre fini d'opérations, on aura : P - A < k , soit : P < T. Mais ceci est absurde car le périmètre p des polygones circonscrits au cercle est supérieur à celui L du cercle. Donc :
C'est dire que P > T. En conséquence : l'aire A du cercle n'est pas inférieure à celle T du triangle.
Conclusion :
le cercle de rayon r a la même aire que le triangle T, c'est à dire 2πr. Bravo Archimède !
➔ Pour en savoir plus :