
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
» polaire d'un point , polaires réciproques | Géométrie projective |
La division harmonique, née du développement de la géométrie projective, fut supprimée des programmes de l'enseignement secondaire lors de l'avènement des mathématiques modernes au début des années 1970. Elle était étudiée dès la seconde et préparait à la difficile étude des sections coniques définies alors dans l'espace par leurs propriétés géométriques où intervenaient les concepts de polaires et de transformations par polaires réciproques introduites par Poncelet. Les sections coniques, étudiées analytiquement en Terminale C puis S en tant que courbes du second degré, ont également disparues des programmes actuels.
A, B, I et J étant alignés, on dit que les points I et J divisent harmoniquement le segment [AB] ou encore que I et J sont conjugués harmoniques par rapport à A et B pour exprimer que le birapport [A,B,I,J] est égal - 1; en d'autres termes :

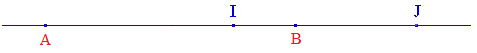
Les mesures algébriques sont ici indispensables. On dit aussi que B (resp. I) est le conjugué de A (resp. J) par rapport à I et J (resp. à A et B). Si A est le conjugué de B, il est clair que B est le conjugué de A. Arithmétiquement, I et J sont les points qui divisent le segment [AB] dans le même rapport AI/AJ = BI/BJ :
Cercle d'Apollonius : »
| Faisceau harmonique de droites concourantes ou parallèles: |
Si quatre droites coplanaires et concourantes en un point O sont coupées harmoniquement par une droite (d), on dit qu'elles forment un faisceau harmonique. O est le centre du faisceau, (OA), (OB), (OI) et (OJ) en sont les rayons. On notera O(A,B ,I ,J) un tel faisceau :

![]()
Si votre navigateur accepte les applets Java
(»
extension CheerpJ![]() )
:
)
:
Vous pouvez déplacer les points
O, A, B et I : la division
"reste" harmonique.
(OB) est la polaire de A par
rapport à I et J
➔ Si les droites sont parallèles, on parle encore de faisceau harmonique (intersection "rejetée" à l'infini).
La conservation du birapport de quatre points permet d'énoncer que :
Toute droite intersectant un faisceau harmonique le divise harmoniquement
On peut vérifier concrètement ce résultat en déplaçant les points A, I, J ou I' de la figure et le prouver afin d'exhiber une intéressante condition d'harmonicité :
Selon la propriété de Thalès, on peut écrire :
IA / IB = OA / KB et JA / JB = OA / LB.
(A,B,I,J) étant harmonique : IA / IB = - JA / JB, ce qui entraîne : OA / KB = - OA / LB et par conséquent : KB = - LB. C'est dire que B est le milieu de [KL]. On en déduit toujours par application de la propriété de Thalès que B' est le milieu de [K'L']; et partant, par un calcul similaire au précédent mais "en sens inverse", on en déduira que la division (A',B',I',J') est harmonique. Le cas d'un faisceau de droites parallèles est trivial. On voit ainsi que l'on peut énoncer :
Quatre droites concourantes (d1,d2,d3,d4) forment un faisceau harmonique si et
seulement si
une parallèle à d1 ou d4 détermine des segments égaux sur les trois
autres.
Application :
On considère un triangle OBC, sa bissectrice intérieure [OC) et sa bissectrice extérieure [OD) qui est donc perpendiculaire à [OC) :

Menons de B la parallèle à [OD) coupant [OA) en E; [OC) est alors perpendiculaire à [EB] et le triangle OEB est donc isocèle puisque ses hauteur et bissectrice principales se confondent. Par conséquent [OC) coupe [EB] en son milieu : d'après le résultat précédent, le faisceau O(A,B,C,D) est harmonique : CA/CB = DA/DB.
➔ On voit ici le lien avec la réflexion en O sur un miroir sphérique d'un rayon incident (AO] se réfléchissant en [OB]. (OI) est alors la normale en O au miroir. Noter aussi la similitude du langage : faisceau harmonique, faisceau lumineux. Descartes fut un ami de Désargues...
Rappelons enfin que des considérations élémentaires montrent que l'on a aussi CA/CB = OA/OB : prolonger [OC), appeler O' le point de [OC) tel que AO = AO'; les droites (OB) et (AO') sont parallèles : appliquer alors la propriété de Thalès "croisée".
∗∗∗
Montrer, en utilisant la propriété de Thalès
qu'un faisceau harmonique de quatre droites parallèles détermine sur
toute sécante à ces droites, une division harmonique.


Géométrie, classe de seconde A' C M, Maurice
Monge, 1958 - Librairie classique Eugène Belin
|
Quelques autres résultats fondamentaux : |
Considérons une division harmonique (A,B,C,D) :

♦ De par la définition du birapport, dire que C et D sont conjugués harmoniques de A et B, c'est dire que C et D divisent le segment [AB] dans le même rapport arithmétique (ou vice versa); en d'autres termes si et seulement si :
![]()
♦ En choisissant une origine quelconque O sur la droite (AB) et en notant a, b, c, d les abscisses respectives de A, B, C, D, on obtient en utilisant la relation de Chasles :
(a + b)(c + d) = 2(ab + cd)
le produit des deux sommes est deux fois la
somme des produits
♦ En choisissant l'origine en A : pour que les point C et D soient conjugués harmoniques de A et B, il faut et il suffit que :
La mesure algébrique de [AB] est donc la moyenne harmonique de celles de [AC] et [AD].
♦ En choisissant l'origine en le milieu I de [AB], on montrera facilement :
![]()

On voit ici que si le point C se rapproche de I, alors IC tend vers 0 et par suite, le produit restant constant, ID tend nécessairement vers l'infini : ainsi lorsque C est au milieu de [AB], D est à l'infini :
Dans
un triangle ABC, si M désigne le pied de la médiane issue de A, alors
A(B, M,
C, d) est un faisceau harmonique

Trapèze et moyenne harmonique (exercice corrigé) : »
| Polaire d'un point par rapport à deux droites : |
On dira que deux points A et B sont conjugués par rapport à deux droites (d) et (d') si (AB) coupe (d) et (d') en deux points I et J tels que (A,B,I,J) soit harmonique. Puisque toute section d'un faisceau harmonique par une droite fournit une division harmonique, on peut se demander quel est l'ensemble des points, conjugués harmoniques d'un point A par rapport à deux droites (d) et (d') et on s'attend à la réponse... : c'est une droite (δ) appelée polaire de A par rapport à (d) et (d').
La construction est très simple et relève d'un résultat remarquable relatif au quadrilatère complet : on a ici (d) = (OI) et (d') = (OJ).
Le cas d'un faisceau parallèle est semblable.

cas sécant
| Polaire d'un point par rapport à un cercle : |
Soit [AB] une corde d'un cercle qui ne soit pas un diamètre. Les tangentes en A et B se coupent en M. Une droite quelconque passant par M, coupe le cercle en C et D et [AB] en N. Dans ces conditions, la division (M,J,C,D) est harmonique :

On dit que les points M et N sont conjugués par rapport au cercle. La droite (AB) est appelée polaire de M par rapport au cercle. Une droite ne passant pas par le centre du cercle est la polaire d'un point M appelé pôle de la droite. Lorsque M est à l'intérieur du cercle, la polaire est à l'extérieur et si M est sur le cercle, la polaire est la tangente en M.
D'une façon générale :
La polaire de M par rapport à un cercle de centre O, de rayon r, est la droite perpendiculaire à (OM) en un point M' tel que :

Preuve : En effet, si T est le point de contact de la tangente passant par M (resp. M'), le triangle OTM (resp. OTM') est rectangle en T. Une propriété élémentaire des triangles rectangles permet d'affirmer que OT2 = OM' × OM. On voit donc que M' est l'image de M dans l'inversion de pôle O, de puissance r2.

»
à distinguer de l'involution ci-après.
| Polaire de deux cercles : |
On appelle parfois ainsi l'axe radical de ces cercles. C'est l'ensemble des points M du plan d'où l'on peut mener à ces cercles des segments de tangente de même mesure.
Cercle polaire : »
| Transformation par polaires réciproques : |
Monge est l'initiateur de cette transformation géométrique dont son disciple Poncelet fera grand usage en géométrie projective : étant donné un cercle (c), dit cercle directeur, on appelle ainsi la transformation qui à tout point M du plan associe sa polaire (p) par rapport à (c).
Si M décrit une courbe (Γ) alors la polaire (p) se déplace en restant tangente à une courbe (γ) appelée transformée de (G) qui est donc l'enveloppe des polaires des points de (Γ).
On démontre alors que (Γ) est l'enveloppe des polaires des points de (γ) : les courbes sont "réciproques", d'où l'appellation transformation par polaires réciproques.
Si quatre points A, B, C et D sont en division harmonique, leurs transformés par polaires réciproques forment un faisceau harmonique. Et réciproquement !
➔ Le cercle (c) peut être plus généralement remplacé par une conique.
| Involution (géométrique) : |
Etant donné une droite (d) et deux points A et B de cette droite, l'application φ qui à tout point M de (d) associe le point M' tel que (A,B,M,M') soit harmonique est une bijection involutive de (d) : elle coïncide avec sa réciproque.
L'introduction géométrique de cette transformation, parfois dénommée involution géométrique, est due à Pappus d'Alexandrie, c'est sans doute la première application involutive (φ = φ-1) de l'histoire des mathématiques si on fait abstraction de x → 1/x.
Si O désigne le milieu de [AB], le point M' est défini par : OM × OM' = OA2, relation qui n'est pas s'en rappeler l'inversion géométrique... A et B sont les points doubles de cette transformation.
Si l'on considère l'ensemble des cercles de diamètre [MM'] lorsque M varie sur (d), on obtient un faisceau linéaire de cercles (les centres sont alignés sur (d). La perpendiculaire à (d) passant par O est l'axe radical du faisceau : tout point de cet axe a même puissance par rapport à tous les cercles :


![]()
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Manip :
double-cliquer sur la figure; choisissez l'icône en forme d'astroïde pour définir le
cercle comme trace.
Cliquer de nouveau sur l'icône puis déplacer M. Rechargez la page pour
retrouver l'image initiale et annuler les sélections.
Inversion géométrique et inversion complexe z' = 1/z : »