
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

On se place ici dans le plan (géométrie plane). Quand on parlera de repère du plan sans autre précision, il s'agira d'un repère orthogonal : les axes sont perpendiculaires ou d'un repère orthonormé : les axes sont perpendiculaires et l'unité de mesure est la même sur chaque axe. Le concept de vecteur remonte à des temps très anciens et fut introduit par les physiciens. On peut estimer qu'Archimède l'utilisa implicitement. Le terme de vecteur est dû à Hamilton.
| Notion élémentaire de vecteur, colinéarité : |
Un vecteur est défini par trois données :

Sur le dessin, on a schématisé quatre vecteurs dont un nommé AB : le point A est son origine, B est son extrémité. Sa direction est celle de la droite (d), son sens de parcours est de A vers B. On dit aussi que (d) est le support du vecteur AB.
La flèche sur le dessin précise le sens du vecteur (de A vers B); la longueur de AB est la distance AB. Dans ce repère orthonormé, l'application du théorème de Pythagore montre que la distance AB est √(42 + 22) = √20 = 2√5.
! Si la flèche était dans l'autre sens, nous parlerions du vecteur BA : qui va de B vers A. Sens contraire mais même direction (d) ! La direction d'une droite, contrairement à une ligne de métro n'est pas liée à son sens de parcours...
➔ Si on se réfère à l'étymologie, la notion de colinéarité nous vient du latin : co = ensemble, linea = ligne, et pourrait signifier sur une même ligne, comme le sont les vecteurs GH et IJ ci-dessous. Mais, en mathématiques, la colinéarité n'exprime que le parallélisme des supports.

Notation, opposé d'un vecteur, vecteur nul :
On connaît la notation [AB] d'un segment, à distinguer de sa longueur AB (sa norme). Pour bien distinguer un vecteur d'un segment, on utilise très souvent, en écriture manuscrite, la notation surlignée fléchée :
![]()
très significative et dénuée de toute ambiguïté, mais peu pratique pour un usage typographique. ChronoMath utilise très généralement la notation gras italique comme vue ci-dessus.
Le vecteur BA a la même direction que AB mais est de sens contraire. On écrira d'ailleurs, comme pour des nombres relatifs : BA= - AB : c'est l'opposé de AB. On peut concevoir un vecteur dont l'origine est confondue avec son extrémité : on parle alors du vecteur nul, que l'on note 0. Par exemple : AA est nul, ainsi que BB . On peut écrire AA = BB = 0.
| Égalité & translation, représentant d'un vecteur : |
Le glissement de A vers B en suivant la direction de la droite (d) s'appelle une translation de vecteur AB et généralement notée tAB.
Vecteur et flèches... : » La translation en tant qu'application affine : »
La translation est une transformation du plan : application bijective du plan sur lui-même. La translation de vecteur transforme un point M en un autre point M' tel que ABM'M soit un parallélogramme.
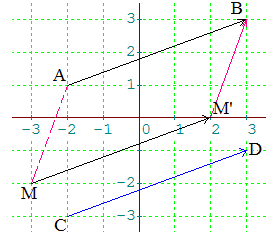
! Attention à l'ordre des points : ci-dessus, ABMM' n'est pas un parallélogramme ! Mais MM'BA désigne le même parallélogramme : la translation qui transforme M en M' transforme A en B : tAB = tMM'
Deux vecteurs sont dits égaux s'ils définissent une même translation. AB et MM' sont égaux et on écrit AB = MM'.
AB = CD ⇔ ABDC est un parallélogramme ⇔ tAB(C) = D
On dira que CD est un représentant d'origine C du vecteur AB.
➔ On dit aussi que les couples de points (A,B) et (C,D), également appelés bipoints, sont équipollents. La relation d'équipollence est une relation d'équivalence. Cette approche des vecteurs par bipoints équipollents était utilisée en classe de 4ème dans les années 1960/80 lors de la très contestée période de l'enseignement des mathématiques "modernes".
» André Lichnerowicz et les mathématiques "modernes"
| Coordonnées d'un vecteur : |
Dans un repère du plan, un vecteur peut être défini par ses coordonnées (on dit aussi ses composantes) : son abscisse et son ordonnée sont mesurées par les nombres correspondant au chemin parcouru dans le sens positif ou négatif pour aller, parallèlement aux axes du repère, de son origine à son extrémité.
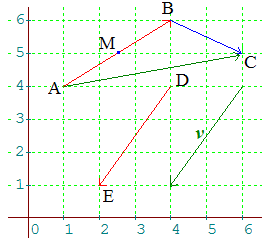
Par exemple, ci-dessus, le vecteur AB a pour coordonnées 3 en abscisse et 2 en ordonnée. Celles de DE sont -2 en abscisse et -3 en ordonnée. On écrira, comme pour un point :
AB(3;2) , DE(-2;-3).
En notant A(xA;yA) et B(xB;yB), on a la formule générale pratique :
AB (xB - xA ; yB - yA)
Avec cette formule, on a BC(2;-1 ) , AD (3;0 ) , AE(1;-3) et v est un représentant de DE, on a v(-2;-3).
➔ deux vecteurs u(x;y) et v(x';y') sont égaux si et seulement si x = x' et y = y'
| Vecteurs et milieu d'un segment : |
Si on place trois points A, B et C dans un repère tels que AB = BC. Que peut-on dire de B pour le segment [AC] ? Réponse B est le milieu de [AC] (ci-dessus à droite). On peut retenir :
M est le milieu de [AB] ⇔ AM = MB
| Addition vectorielle, règle du parallélogramme, formule de Chasles, composée de deux translations : |
L'addition de deux vecteurs du plan se fait selon la règle connue en sciences physiques pour exprimer la résultante de deux forces : si u et v sont deux vecteurs de représentants AB et CD, on "recopie" CD en BE, représentant de v d'origine B. Le vecteur somme s est AE.
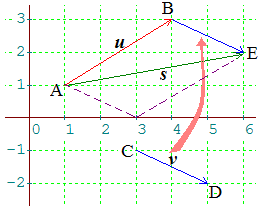
On remarque que si l'on avait recopié v en choisissant un représentant d'origine A, on aurait pu remplacer u par un représentant d'extrémité E. Cela permet de remarquer :
que la somme de deux vecteurs est commutative : u + v = v + u
qu'en choisissant u et v de même origine (A dans notre exemple), lorsque u et v n'ont pas la même direction, le vecteur somme s est représenté par la diagonale d'origine A du parallélogramme construit sur les vecteurs u et v.
Ce dernier résultat est une méthode de construction de la somme dite règle du parallélogramme. Elle coïncide avec la règle de composition des forces concourantes qu'énoncèrent des physiciens comme Stevin, Roberval ou Varignon.
Cas de deux vecteurs colinéaires : AB et CD ont même direction. On "recopie" CD en BE; la somme est AE et il y a deux cas suivant que les vecteurs ont même sens ou non. A gauche ci-dessous, les vecteurs AB et CD ont même sens. A droite, ils sont de sens contraire. Les avoir choisis "horizontaux" ne restreint pas la généralité !
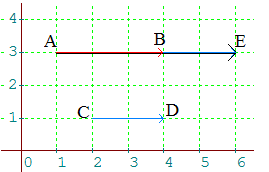
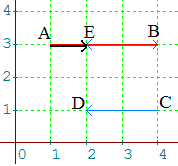
➔
On peut tout aussi
bien recopier AB en DF (schéma de droite); la somme
est alors CF.
On remarque que CF = AE : ce qui montre que l'addition est commutative : AB + CD = CD + AB.
Noter aussi, et c'est heureux, que la somme ne dépend pas des représentants choisis pour effectuer l'addition.

La règle de construction de la somme de deux vecteurs permet d'énoncer la formule de Chasles (on peut considérer le schéma ci-dessous) :
Pour tout triplet (A,B,C) de points du plan : AB + BC = AC
➔ En termes de translation et de composition des applications, l'addition vectorielle exprime que tAB o tBC = tAC et que cette composition est commutative : tu o tv = tv o tu= tu + v.
| Coordonnées du vecteur somme : |
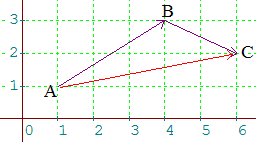
Le schéma ci-dessus indique que AC = AB + AC. On a : A(1,1) , B(4,3) , C(6,2). Donc : AB(3,2) , BC(2,-1) , AC(5,1). Le schéma, associé à la définition des coordonnées d'un vecteur, montre que :
Si u(x,y) et v(x',y'), alors s(x + y, x' + y')
| Multiplication d'un vecteur par un nombre (multiplication scalaire) : |
Il est naturel de poser v + v = 2v et si v(x;y), le vecteur w = 2v aura pour coordonnées (2x;2y). Plus généralement, si v(x;y), le vecteur k.v où k désigne un nombre quelconque sera le vecteur w de coordonnées (kx;ky). C'est un vecteur colinéaire à v.
La notion d'espace vectoriel : »
∗∗∗
a/
On considère les trois points A, B et C ci-dessus.
☼
Calculer les coordonnées du
point D afin que,
dans cet ordre, ABCD soit un parallélogramme.
b/
Calculer les coordonnées du point D' afin que, dans cet ordre, ABD'C soit un
parallélogramme.
➔ Pages rattachées (entre autres) :