ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
C'est dans sa Dioptrique, traité relatif à l'étude de la réfraction de la lumière, que Descartes introduit les ovales qui portent son nom. Les ovales de Descartes sont aussi nommés courbes aplanétiques (en grec et mot à mot : sans errements) : considérons un système optique centré (s) et un objet [AB] normal à son axe d'image [A'B'].
(s) est dit aplanétique si pour tout point M de [AB] , un rayon passant par M et traversant (s) passe par M', image de M : on dit alors que M et M' sont stigmatiques (du grec stigma = point; l'image d'un point est le point image).
» Notons que planète provient du grec planêtês signifiant errant, qui fournit également erreur : celui qui se trompe n'est pas dans le bon chemin, il erre dans l'erreur... Quant aux ovales, on verra dans la suite que l'appellation n'est pas très appropriée.
Ove, ovales (les vrais...) : »
Étude des "ovales" de Descartes
Étant donnés deux points fixes F et F' d'un plan (P), Il s'agit de rechercher l'ensemble des points M de (P) tels que :
aMF + bMF' = k
où a, b et k sont des constantes données non nulles.
C'est en quelque sorte une généralisation de la définition bifocale des coniques (pour k > 0, si a = b > 0 : ellipse, si b = -a < 0 : hyperbole). On voit donc que l'appellation ovale n'est pas vraiment adéquate...
Si on appelle foyers les points F et F', Chasles montra que les ovales de Descartes en possèdent un troisième F". L'ovale peut être défini par deux quelconques de ces foyers et lorsque | a/b | tend vers 1, alors ce troisième foyer s'éloigne à l'infini : on retrouve les coniques.
On pourrait tenter d'étudier ces ensembles de points au moyen de leur équation cartésienne mais ce serait très lourd du fait de a et b généralement distincts. On lève la difficulté en posant r = MF, r' = MF' avec la possibilité d'avoir r et r' non positifs : ar + br' = k.
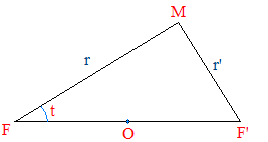
C'est une définition bipolaire de l'ensemble cherché et on se ramène pour l'étude et le tracé à une équation polaire en choisissant F comme pôle (origine) et en exprimant r' en fonction de r. Selon Al Kashi, on peut écrire :
➔
Dans les exemples suivants, on
choisit OF comme unité de mesure. Ainsi, dans un repère
d'origine O, nous prenons F(-1;0) et F'(1;0). Dans ces conditions,
FF' = 2; on aura alors :
La transformation utilisée (passage au carré) n'étant pas régulière, on devra être prudent dans l'analyse des résultats graphiques : contrôle de la positivité de r' et de r. Comme le pôle est pris en F(-1,0) , les courbes tracées par l'ordinateur seront "décalées" par translation de vecteur v(1,0); on rétablit aisément la "réalité" en translatant pareillement l'axe des ordonnées.
| Étudions le cas simple r + r' = 3 : |
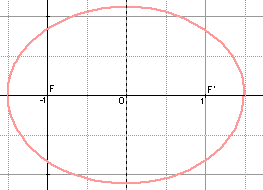
On a dit précédemment que nous devrions obtenir une ellipse. L'équation (e) devient ici (3 - r)2 = r2 + 4 - 4rcos t. Les r2 s'éliminent; on obtient : r = 5/(6 - 4cos t) : on reconnaît l'équation polaire d'une ellipse qui s'écrit généralement sous la forme :
![]() ,
t décrivant [0;2π], e < 1
,
t décrivant [0;2π], e < 1
p est le paramètre et e est l'excentricité. Quitte à poser T = π - t, on obtient cette forme pour T décrivant [-π;+π] avec p = 5/6 et e = 2/3. On retrouve cette valeur sur le graphique : e = c/a où c désigne l'abscisse de F' et a le demi-grand axe. Noter que p = b2/a, b désignant le demi petit axe : b2 = 5/3 ≅ 1,29.
| Un autre cas élémentaire : r - r' = 1 |
Nous devons ici retrouver une hyperbole. On a r' = r - 1 que nous reportons dans (e), ce qui fournit l'équation polaire :
r = 3/(4cos t - 2)
L'équation polaire de l'hyperbole est de la forme indiquée ci-dessus avec e > 1. On change t en π - t, puis r en -r; l'équation devient
r = 3/2/(1 + 2cost)
L'excentricité est e = 2 = c/a; le paramètre est p = 3/2 = b2/a. On obtient a en t = 0 (sommet d'abscisse positive) : a = 1/2. D'où c = 1 et b = √3/2. Ce qui équivaut sous la forme cartésienne à x2 - y2/3 = 1/4 :
| Un cas plus délicat : 2r + r' = 4 |
On a ici r' = 4 - 2r, soit : (4 - 2r)2 = r2 + 4 - 4rcos t , selon l'équation générale (e) ci-dessus. On développe, on réduit. On obtient une équation du second degré en r. On pose alors b(t) = 8 - 2cos t, puis Δ = b2(t) - 36. Dans ces conditions :
r = [b(t) ± √Δ]/3 avec (positivité) : 0 ≤ r ≤ 2
La courbe obtenue est un très beau limaçon de Pascal :
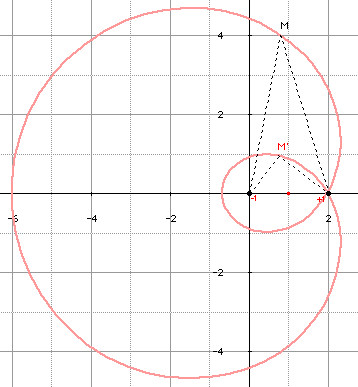
➔ Un point comme M', sur la petite boucle est obtenu par r = [b(t) - √Δ]/3. En rouge : les abscisses après translation. Seule la petite boucle convient. Un point comme M ne convient pas : c'est en fait un point de 2r - r' = 4.
| Un cas plus compliqué : 3r + 2r' = 12. Nous avons là : |
r = (9 - 2cos t ± √Δ)/1.25 → 1.25 = 5/4 (pour simplifier l'écriture)
avec Δ = (9 - 2cos t)2 - 40, sous la condition r et r' positifs, soit : 0 ≤ r ≤ 4. Seule l'ovale intérieur convient ici : cas r = (9 - 2cos t - √Δ)/1.25. La partie extérieure correspond à 3r - 2r' = 12.