ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Abscisse, ordonnée, coordonnées selon d'Alembert
    (Dictionnaire raisonné des Sciences, des Arts et des Métiers)             » La notion moderne de repère et de coordonnées

 ➔   Texte original. Seuls sont modifiés la mise en page, quelques tournures et aspects orthographiques ou grammaticaux Les mots ou les commentaires en vert sont ajoutés pour une meilleure compréhension.

ABSCISSE, s. f. (substantif féminin) est une partie quelconque du diamètre ou de l'axe d'une courbe, comprise entre le sommet de la courbe ou un autre point fixe et la rencontre de l'ordonnée. Telle est la ligne AE comprise entre le sommet A de la courbe et l'ordonnée EM. On appelle les lignes AE abscisses, du latin abscindere, couper, parce qu'elles sont des parties coupées de l'axe ou sur l'axe (...).

» abscindere a pour participe passé abscissum. Mais on peut aussi estimer que abscisse provient de ab, préposition marquant une séparation et scindere = diviser, morceler, dont le participe passé est scissum. Le terme fut utilisé par Newton (1686). Il apparaît dans le Dictionnaire des termes d'Arts et de Sciences de Thomas Corneille (frère de Pierre, le célèbre poète dramatique français) en 1694.

»  Selon d'Alembert, une troisième proportionnelle à deux nombres a et y est le nombre x tel que a/y = y/x, ce qui équivaut ici à y2 = ax, équation de la parabole ci-dessus en prenant le sommet A comme origine. Les cas de l'ellipse et de l'hyperbole sont aussi évoqués.

ORIGINE, en Géométrie, se dit du point par lequel on commence à décrire une courbe, lorsqu'on la décrit par un mouvement continu. On appelle aussi assez souvent origine de la courbe son sommet, c'est-à-dire le point A (ci-contre) où l'on suppose que commencent les ordonnées et les abscisses.

ORDONNÉE, s. f. (substantif féminin) c'est le nom qu'on donne aux lignes tirées d'un point de la circonférence d'une courbe à une ligne droite, prise dans le plan de cette courbe et qu'on prend pour l'axe, ou pour la ligne des abscisses. Il est essentiel aux ordonnées d'être parallèles entre elles. On les appelle en latin ordinatim applicatae (mot à mot : régulièrement placées); telle est PM.

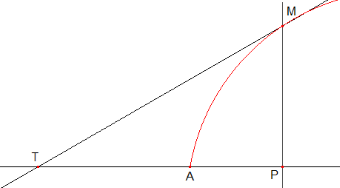
» sur la figure d'Alembert considère AP comme l'abscisse de M, et PM son ordonnée. (MT) représente la tangente en M à la courbe. Il semble que Pascal fut le premier à utiliser ce terme.

Quand les ordonnées sont égales de part et d'autre de l'axe, on prend quelquefois la partie comprise entre l'axe et la courbe pour demi-ordonnée et la somme des deux lignes pour l'ordonnée entière (...).

Il n'est pas essentiel aux ordonnées d'être perpendiculaires à l'axe, elles peuvent faire avec l'axe un angle quelconque, pourvu que cet angle soit toujours le même (...).

COORDONNÉES, adj. pl. (Géom.) on appelle de ce nom commun les abscisses et les ordonnées d'une courbe, soit qu'elles fassent un angle droit ou non. La nature d'une courbe se détermine par l'équation entre ses coordonnées. Voyez COURBE. On appelle coordonnées rectangles, celles qui font un angle droit.

  Jean le Rond d'Alembert

» Selon Florian Cajori, historien des sciences, le concept fondamental de coordonnées remonte à Leibniz en 1692.

La notion de coordonnées de nos jours :      

♦ Dans le plan, on se donne deux droites (x'x) et (y'y) sécantes en un point O appelé origine, munies chacune d'un vecteur directeur, (OI et OJ), indiquant l'unité et le sens de la graduation choisis sur ces deux droites prenant le nom d'axes de coordonnées. Le triplet (O, OI, OJ) est qualifié de repère cartésien , du nom de René Descartes, à qui l'on doit les prémisses de la géométrie analytique. Très généralement, ces axes sont perpendiculaires mais ce n'est pas une obligation, tout dépend du problème étudié. Si tel est le cas, on parle de repère orthogonal. Si, de plus, les vecteurs ont la même longueur (même norme), on parle de repère orthonormé. L'axe (x'x) est celui des abscisses, l'axe (y'y) est celui des ordonnées avec le sens étymologique exposé ci-dessus par d'Alembert.

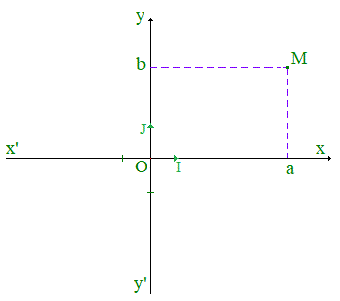
♦ Dans l'espace 3D, on se donne trois droites distinctes (x'x), (y'y), (zz') sécantes en un point O pris comme origine. Le troisième axe (zz') indique la hauteur d'un point M par rapport au plan (Ox,Oy) souvent qualifié de plan horizontal. Le vecteur OK indique l'unité utilisée. Cette hauteur est la cote de M, lequel se projette sur (Ox,Oy), parallèlement à (Oz), en le point m(a,b).

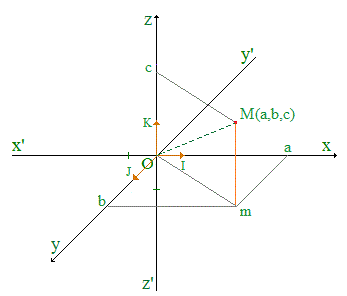
 ➔  Lorsqu'un repère du plan est défini par trois points non alignés, par exemple (O,A,B), on parle de repère affine. Dans ce cas OA joue le rôle de OI et OB celui de OJ. Dans l'espace, il s'agira de quatre points non coplanaires (O,A,B,C), où (O,A,B) est un repère affine du plan "horizontal" et C hors de ce plan.

Dans la pratique, on se contente souvent de ne présenter que les graduations utilisées sur chaque axe. Par exemple dans le cas d'un repère du plan :

Droites du plan et de l'espace : »   |   La notion de vecteur : »   |   Espaces affines : »  |  Espaces vect. normés : »

Coordonnées sphériques, paramétriques, cylindriques, géocentriques, ... : »

 ➔  Pour en lire ou savoir plus :

© Serge Mehl - www.chronomath.com