ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Les ensembles selon Cantor,
vocabulaire élémentaire les aspects logiques et contradictoires |
Qu'est-ce qu'un ensemble ?
Selon Cantor, il s'agit « d'une pluralité (d'objets) pouvant être pensée comme une unité, autrement dit toute collection d'objets déterminés pouvant être réunie en un tout par une loi (un critère) ».
Reconnaissons que c'est assez flou... Considérons une propriété P clairement énoncée (sans ambiguïté) portant sur des objets eux-mêmes bien définis. Si x est un objet pour lequel la propriété est vérifiée, nous dirons que x est un élément de la collection considérée. Les éléments vérifiant P constituent un ensemble que nous notons E.
Pour signifier l'appartenance à E d'un élément x, on écrit : x∈E. Le signe ∈se lit "appartient à " ou "est élément de". Pour désigner les éléments d'un ensemble E, on peut écrire ces éléments entre accolades :
Exemple 1 : Soit E l'ensemble des multiples de 5 inférieurs à 33. On a E = {0 , 5 , 10 , 15 , 20 , 25 , 30}. Si E possède une infinité d'éléments, on peut aussi écrire, à condition que ce soit clair pour le lecteur : E = {0 , 1 , 2 , 3 , ...} , F = {1 , 3 , 5 , 7 , ...}. On exprime ici l'ensemble N des entiers naturels et celui des entiers impairs.
Un ensemble contenant un seul élément est appelé singleton. E = {0} est le singleton dont l'élément est zéro.
L'ensemble G constitué des entiers appartenant à la fois à E et F (exemple 1 ci-dessus) ne contient aucun élément. On dit que G est vide ; on peut écrire G = {}. L'ensemble vide ne prendra le statut d'ensemble qu'avec la notation Ø due à Weil et l'équipe Bourbaki vers 1939.
Exemple 2 : Soit E = {a , b , c}; ses parties sont {a} , {b} , {c} , {a , b} , {a , c} , {b , c} , {a , b c}. Il en manque une ? Oui, bien sûr : Ø, la partie vide ! On apprendra ici que si E possède n éléments, alors il contient 2n parties. Par exemple, si F = {0, 1 , 2 , 3 , ... , 10}, F possède 1024 parties : sacré boulot que de les donner toutes...
Définition en extension et en compréhension :
Ci-dessus, les éléments de E et F sont donnés explicitement (malgré les pointillés concernant F) : on dit qu'ils ont été définis en extension. On peut aussi les définir en compréhension en donnant la (les) condition(s) discriminantes :
Exemple 3 : Soit encore F = {0, 1 , 2 , 3 , ... , 10}; G = {x∈F, x multiple de 3}, H = {x ∈ F, x multiple de 7, x ≠ 7}. F est donné en extension et G et H en compréhension. On déduit des définitions de G et H que G = {0, 3, 6, 9} et H = Ø.
Comme l'évoqua Cantor, on doit distinguer entre un ensemble bien défini par un critère et un ensemble dont on ne saura dire si te ou tel élément connu lui appartient ou non eu égard au niveau de connaissances mathématiques lors de son étude à une époque donnée :
En 1874, année de la première publication de la théorie des ensembles, on savait depuis quelques mois, grâce à Hermite que le nombre e, base des logarithmes népériens, est transcendant mais on ne savait pas si π était algébrique ou non. Sa transcendance fut établie par Lindemann en 1882. Donc parler de l'ensemble des nombres algébriques en 1874 laissait planer un doute et ce doute persiste aujourd'hui pour d'autres nombres, comme la constante d'Euler.
Sous-ensemble (ou partie) :
Une partie de E ou un sous-ensemble de E est constitué(e) de certains éléments de E désignés au moyen d'une propriété supplémentaire discriminante. Si on note A cette partie, on écrit A ⊂ E : A est contenu dans E. On dit aussi que E contient A et on peut écrire E ⊃ A. On voit l'analogie avec les signes ≤ et ≥.
Exemple 4 : Dans l'exemple 3 ci-dessus, on a G ⊂ F. Soit maintenant E l'ensemble des multiples de 5 et A celui des multiples de 10. On a A ⊂ E. On peut définir E par «l'ensemble des entiers naturels dont le chiffre des unités est 0 ou 5» et A par «l'ensemble des éléments de E dont le chiffre des unités est nul».
» Peano , Charles S. Peirce , Schröder | de Morgan , Venn
Intersection et réunion de deux parties :
L'intersection de deux parties est la partie constituée des éléments communs. Cette intersection peut être vide comme constaté dans l'exemple 1. On note A∩B, et on lit A inter B, l'intersection de A et B.
La réunion de deux parties la partie constituée des éléments communs ou non. Cette intersection peut être vide comme constaté dans l'exemple 1. On note A∪B, et on lit A union B, la réunion de A et B.
Complémentaire, partition :
Dans un ensemble E contenant une partie A, on peut
s'intéresser aux éléments de E qui ne sont pas éléments de A : on parle du
complémentaire de A dans E souvent noté
EA
ou simplement
A s'il n'y a pas d'ambiguïté (notation
de Bourbaki). Pour des raisons
pratiques rédactionnelles, on fera usage sur ce site de CA
ou encore
A si pas d'ambiguïté avec l'adhérence
de A (concept topologique) ou négation de la proposition A dans le contexte
de logique propositionnelle.
On peut écrire, dans ce cas ensembliste :
A = { x∈E, x∉A }
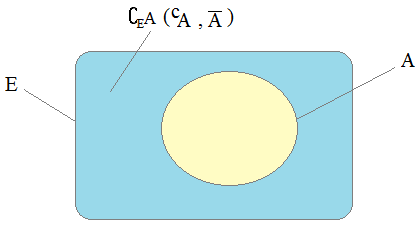
» Algèbre de Boole , lois de Morgan , logique d'Aristote
Lorsque la réunion de parties non vides d'un ensemble non vide E est égal à E et que l'intersection deux à deux de ses parties est vide, on dit que l'ensemble de ces parties forment une partition de E.
Exemple 5 : Si A est une partie non vide d'un ensemble E, l'ensemble {A , A} constitue une partition de E. Dans l'ensemble N des entiers naturels, il en est ainsi des nombres pairs et impairs. Les ensembles de nombres de la forme 3n, 3n+1 et 3n+2 constituent une partition de N.
! Si E est l'ensemble des voyelles, E = {a , e , i , o , u ,y }, le complémentaire de A = {i , y} dans E est A = {a , e , o , u}, mais si E est l'ensemble des lettres de l'alphabet, on comprendra que le complémentaire n'est pas le même.
Exemple 6 : Soit A = {a , b , c}; et B = {c , d , e }. A ∩ B = {c} , A ∪ B = {a , b , c , d}. Écrire {c , c} est incorrect : {c }∪{c } = {c}. On ne distingue pas entre deux éléments identiques. Posons E = {a , b , c , d} et D = {b , c}. Dans l'ensemble E, D = {a , d}.
∗∗∗
Dans un ensemble E, on considère deux parties A et B.
Montrer que si A ⊂
B alors CAP
⊂
CBP pour toute partie P
de E
Diagrammes de Venn : » Notations ensemblistes de Peano : » » De Morgan
Ensembles et logique :
Considérons l'ensemble des nombres entiers naturels inférieurs à 50, de la forme 6k ±1 où k désigne un entier naturel. Il ne semble pas y avoir là ambiguïté d'aucune sorte; si E désigne l'ensemble des nombres ainsi désignés :
E = {1, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35, 37, 41, 43, 47, 49}
Notons P la propriété « être un entier naturel inférieur à 50 dont le reste, dans la division par 6, est 1 ou 5 » et décidons de noter P(x) la proposition (prédicat) « la propriété P est vérifiée par x ». On peut écrire, en utilisant le signe ⇔ d'équivalence logique pour signifier « si et seulement si » :
x∈E ⇔ P(x)
Soit maintenant Q la propriété « être un entier naturel premier dont le reste, dans la division par 6, est 1 ou 5 ». Soit F l'ensemble constitué des nombres premiers de E :
F = {5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47}
P(x) ∧ Q(x), conjonction de P(x) et Q(x) revient à exprimer que x∈F :
x∈F ⇔ P(x) et Q(x)
Tout cela semble bien clair et parfaitement logique. Et pourtant...
| Le début des ennuis... : |
Il s'agit de bien distinguer appartenance et inclusion : Si E = {a , b , c} , a∈E mais il est tout à fait incorrect et faux d'écrire a ⊂ E car a n'est ni un ensemble ni un sous-ensemble de E (partie), c'est un élément de E. Par contre, on écrira {a}⊂E : le singleton {a} est une partie de E.
Ce vocabulaire étant défini et bien compris, exposons maintenant une anomalie logique inquiétante mise à jour par Cantor lui-même en 1889 :
On peut imaginer l'ensemble X de tous les ensembles (en tant que
collection de tous les ensembles imaginables).
Mais est-ce vraiment un
ensemble ?
Si oui, X est un élément de X : X∈X : c'est ennuyeux eu égard à qui vient d'être dit, on ne peut donc pas accepter X en tant qu'ensemble au sens mathématique.
Décidons alors qu'une collection d'objets ne peut avoir le statut d'ensemble s'il se contient lui-même comme élément et considérons W l'ensemble de tous les ensembles qui ne se contiennent pas eux-mêmes :
| A-t-on W∈W ? |
|
La proposition W∈W ne semble donc pas répondre au principe du tiers exclu oui/non, VRAI/FAUX, principe qui sera d'ailleurs remis en cause par Brouwer et le courant intuitionniste l'année de la mort de Cantor. En fait, ici, ce n'est pas le tiers exclu qui est en cause mais la bonne définition d'un ensemble qui n'est donc pas si simple que l'on pourrait croire a priori.
Russel et les paradoxes de la théorie des ensembles : »
Face à ces difficultés, Zermelo tentera (1908) de donner une définition axiomatique mais il engendra la fameuse bataille de l'axiome du choix...
Zermelo et l'axiome du choix : »
|
Ensemble produit, paire, couple et coordonnées cartésiennes : |
L'application qui à tout couple (E,F) d'ensembles, associe l'ensemble E × F, ensemble des couples (x,y) où x est élément de E et y élément de F est appelé produit cartésien de E par F, cartésien en l'honneur de Descartes à qui on accorde généralement la paternité des coordonnées (voir ci-après). Ce "produit" pourrait être considéré comme une loi de composition interne dans l'ensemble des ensembles. Hélas, ce dernier ensemble n'est pas un ensemble...
Le produit cartésien E × F de deux ensembles est cependant une notion première et il convient de distinguer E × F et F × E :
! Dans un couple l'ordre des éléments le constituant est primordial. Ce n'est pas le cas dans une paire : {x,y} = {y,x}. Une paire est un ensemble constitué de deux éléments (c.à.d. de cardinal 2).
Kuratowski et définition ensembliste d'un couple : »
On apprend au collège à bien distinguer sur un graphique des points comme M(2;3) et P(3,2) : confusion classique entre abscisse (x : coordonnée "horizontale") et ordonnée (y : coordonnée "verticale"). On parle de coordonnées cartésiennes pour rappeler que Descartes fut un pionnier en ce domaine.
Dans un repère orthonormé (axes perpendiculaires et unité commune sur les axes), ces points sont symétriques par rapport à la bissectrice du repère. On note l'abscisse en premier !
dans le plan dans l'espace
➔ Rappelons que dans l'espace (3 dimensions), un point est repéré par ses coordonnées "horizontales" x et y dans le plan (Ox,Oy) et sa coordonnée verticale : sa cote z. Sur le dessin ci-dessus, on a M(20,17,35).
| L'ensemble N des entiers naturels est-il clairement défini ? |
Qu'est-ce qu'un entier naturel ? le concept restait intuitif depuis l'aube de l'humanité. Est-ce donc un objet mathématique bien défini ? Peut-on parler de l'ensemble des entiers naturels ? Délicat, car cet ensemble n'est pas limité : il possède une infinité d'éléments. On ne peut donc pas l'écrire in extenso comme dans les exemples E et F ci-dessus.
D'où la nécessité dans la théorie des ensembles, pour une théorie mathématique rigoureuse, d'une construction méthodique des ensembles de nombres. Pour la construction de N, ensemble des entiers naturels, première pierre de l'édifice mathématique, Peano et Von Neumann adoptèrent une méthode due à Pascal : le raisonnement par récurrence rebaptisé pompeusement raisonnement par induction transfinie.
➔ Pour en savoir plus :
Eléments de Mathématique, Livre I, Théorie des ensembles, Nicolas Bourbaki, Ed. Hermann
La théorie des ensembles, par Alain Bouvier - Que sais-je ?, n° 1363, P.U.F.
Théorie des ensembles , cardinaux, ensembles
ordonnés et nombres ordinaux, par E. Kamke
Ed. Dunod, monographies, Paris - 1964.
Clifford
