Trifolium

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Trifolium régulier » Folium , Bifolium , Quadrifolium

Rosace à trois branches isométriques dont une équation polaire est :

r = a.cos 3t (e1)

C'est un cas particulier de rosace de Grandi. Il est aussi la podaire de la deltoïde par rapport à l'origine où l'on montre que l'équation (e1) est équivalente à :

x = a(cos2t - cost)/2 , y = a(sin2t + sint)/2

Le trifolium est tracé ci-dessous pour a = 1 :

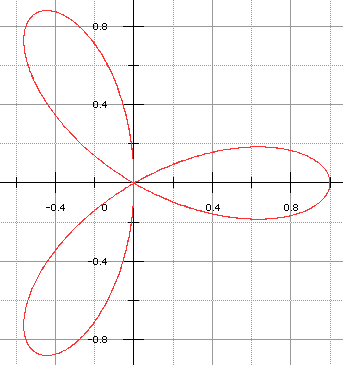
Son étude a théoriquement lieu sur [0,2π] ou bien [-π,+π] mais le changement de t en - t laisse r inchangé : on peut se restreindre à [0,π]. On remarque aussi que r(2π/3 + t) = r(t) : les 3 pétales s'obtiennent donc par rotation de l'une d'elles de 120°.

∗∗∗
Montrer que l'on peut se contenter d'une étude sur [0,π/6] et de compléter par symétrie par rapport à Ox puis par rotations d'angle 2π/3.

Le trifolium est une courbe algébrique de degré 4 (quartique bicirculaire).

Équation cartésienne implicite :

Connaissant cos2t = 2cos²t - 1 et cos(a + b) = cosa.cosb - sina.sinb, en écrivant cos3t = cos(2t + t), on obtient facilement cos3t = 4cos³t - 3cost. Or x = r.cost et y = r.sint. En supposant provisoirement que r est non nul, on a cost = x/r, ce qui conduit à :

r/a = 4x³/r³ -3x/r = 4x³/r³ -3xr²/r³, soit r⁴ = a[4x³ - 3x(x² + y²)] = ax(x² - 3y²). C'est à dire :

(x² + y²)² - ax(x² - 3y²) = 0

Équation paramétrique :

Partant de l'équation x = a(cos2t - cost)/2 = a(2cos²t - cost - 1)/2 , y = a(sin2t + sint)/2 = a(2sintcost + sint)/2, on pose u = tan(t/2). Un calcul élémentaire reposant sur les expressions rationnelles de cost et sint conduit à :

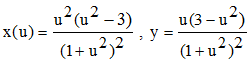
➔ On voit clairement sous cette forme que le trifolium est une courbe unicursale admettant l'origine O(0,0) comme point triple (u =0 et u = ±√3).

Aire du trifolium :

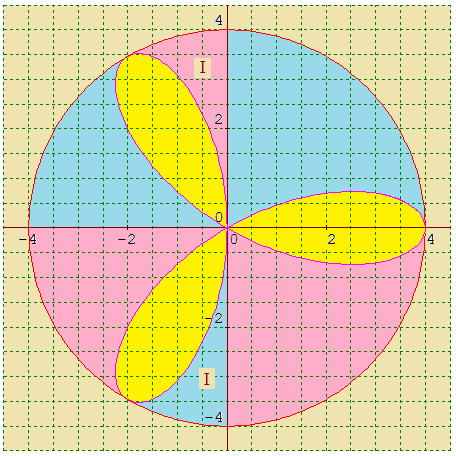
L'aire du trifolium régulier, πa²/4, est le quart du disque dans laquelle il s'inscrit. Vous établirez très facilement ce résultat en calculant l'intégrale :

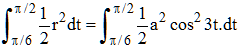
relative à l'aire intérieure (Rép. : πa²/12) du pétale sud-ouest correspondant à t variant de π/6 à π/2, en remplaçant cos²3t au profit de ½(cos6t + 1).

∗∗∗
Quelle est l'aire d'un domaine comme I ci-dessous ? Rép. : πa²/24.

» Folium simple , Bifolium , Triscèle , Quadrifolium , Folium de Descartes , Trisectrice de Longchamps