ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Notion d'homologie (géométrie projective)            » Chasles ,  Desargues , Poncelet , géométrie projective

 ➔  On définit ici une homologie plane; on définirait l'homologie dans l'espace 3D en remplaçant la droite (d), dont il est fait état ci-dessous, par un plan (P). Cette homologie géométrique est à distinguer de l'homologie algébrique rencontrée en topologie.

Considérons une droite (d) et un triplet (O,A,A') de points alignés, (OA) non parallèle à (d), A et A' n'étant pas situés sur (d). à tout point M du plan non situé sur (OA) associons le point M' tel que M' = (OM) ∩ iA' avec i = (AM) ∩ (d).

» Notons qu'un cas comme (AM)//(d) n'est pas un problème en géométrie projective : i est rejeté à l'infini et par suite, M' est obtenu par intersection de (OM) avec la parallèle à (d) passant par A'.

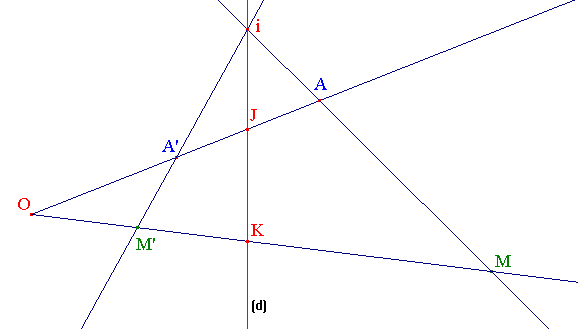
Il est clair que :

• l'image d'une droite (AB), B non situé sur (OA), est la droite (A'B').

• tout point de (d) non situé sur (OA), est invariant.

On peut alors prolonger la définition en construisant l'image d'un point B de (OA) en remarquant que u = (BM) ∩ (d) est invariant. Le même principe (d'alignement) conduit à l'invariance de J.

Des droites comme (AM) et (A'M') sont dites homologues et l'application qui à tout M du plan, autre que O, associe M' est appelé homologie de centre O, d'axe (d), définie par A et A'.

Considérons le faisceau i(OJAA') et le birapport des quatre points O, J, A, A'; l'invariance du birapport par projection centrale montre que pour tout point M du plan, le birapport [O,K,M,M'] est une constante k. On parle alors du rapport k de l'homologie.

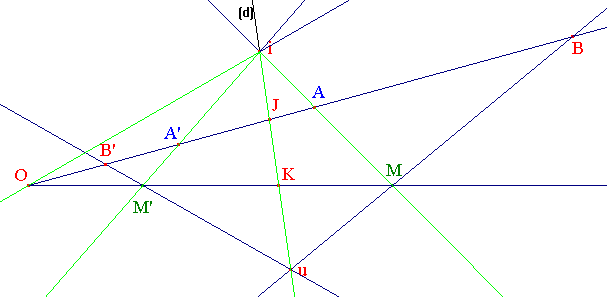
 ➔  On remarquera que deux figures homologues ont même perspective de centre O sur l'axe (d) de l'homologie.