ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Inversion géométrique       » courbes anallagmatiques        » De son origine , expression analytique réelle et complexe , point à l'infini , involution géométrique , construction de Napoléon

Un nombre k non nul (puissance de l'inversion) et un point O (pôle) étant donnés, à tout point M du plan ou de l'espace 3D euclidien autre que O, noté E*, on peut faire correspondre un point M' tel que :

O, M et M' sont alignés et  OM.OM' = k     (d1)

Notons T cette transformation. Elle est manifestement une bijection involutive de E* (elle coïncide avec sa réciproque) : si M'' est l'image de M', on aura  OM'.OM'' = k et par suite OM'' = OM, donc M" = M. En d'autres termes T = T^-1 ou encore T o T = id, ou encore :

M' = T(M) ⇔ M = T(M')

 ➔   On remarquera que la définition (d1) est équivalente à la relation vectorielle :

♦  Points invariants, cercle d'inversion :    

L'ensemble des points M invariants par T vérifient OM² = k : cet ensemble est donc non vide si et seulement si k > 0 et il s'agit dans le plan (resp. l'espace) d'un cercle (resp. d'une sphère) de centre O de rayon √k. On parle de cercle d'inversion (resp. sphère d'inversion), permettant de caractériser l'inversion T :

Tout cercle de centre O de rayon r définit une unique inversion de pôle O de rayon √k

• Remarquer que tout point (autre que O) situé à l'intérieur du cercle (resp. de la sphère) d'inversion
  a son image à l'extérieur, et vice-versa.

• L'égalité  OM.OM' = (√k)² montre que les points M et M' sont conjugués par rapport au cercle d'inversion : la polaire de M est la droite perpendiculaire à (OM) passant par M'.

∗∗∗
Montrer que si M' et M'' sont les images respectives de M par l'inversion de même pôle O, de puissance k et k',
alors M'' est l'image de M' par l'homothétie de entre O, de rapport k.

On déduit de ce résultat que l'inversion de rapport -k peut s'écrire comme composé de l'inversion de rapport k suivie de la symétrie par rapport au pôle O. Plus généralement, avec des notations relativement évidentes :

inv_O,k = hom_O,k o inv_O,1

Dans toute la suite, on se restreint à k > 0 et à l'étude des inversions du plan dont les propriétés se généralisent facilement à l'espace. Voir en particulier : projection stéréographique, sphère de Riemann, expression analytique.

♦  Une propriété caractéristique de l'inversion :            

Deux figures (F) et (F') se correspondent par inversion si deux points A et B quelconques de (F) et leurs images A' et B' de (F') sont cocycliques (situés sur un même cercle). On a alors :

Ce résultat apparaît bien évident si l'on connaît la notion de puissance d'un point par rapport à un cercle.

♦  Relation entre les distances de deux  points et de leurs images par inversion :     

Si M et N sont deux points du plan, M' et N' leurs images dans une inversion de pôle O, de puissance k, alors :

Preuve : On a OM.OM' = ON.ON' = k. Reportons [OM] en [OM₁] sur [ON) et [ON] en [ON₁] sur [OM). Il vient OM₁.OM' = ON₁.ON' = k, donc ON₁/OM' = OM₁/ON' : les triangles OM₁N₁ et OM'N' sont donc semblables. On en déduit : MN/M'N' = M₁N₁/M'N' = ON₁/OM' = ON/OM' = (ON × OM)/(OM' × OM) = ON × OM/k².

Les triangles OMN et OM₁N₁ étant isométriques, on peut aussi retenir que :

Si M et N sont deux points du plan, d'images respectives M' et N' dans une inversion de pôle O, de puissance k, les triangles OMN et OM'N' sont semblables dans le rapport MN/M'N' = ON × OM / k².

♦  Conservation du birapport de quatre points alignés :    

Si A, B, C, D sont quatre points du plan, alors les birapports de ces points et de leurs images respectives A', B', C', D sont égaux : [A, B, C, D] = [A', B', C', D']. En particulier, si la division [A, B, C, D] est harmonique (birapport = -1), il en est de même de [A', B', C', D'].

Preuve : En écrivant [A, B, C, D] sous la forme produit, c'est à dire CA × DB / DA × CB, on obtiendra facilement la preuve de ce résultat en appliquant le précédent.

La division harmonique (autrefois au programme de seconde...)  :  »

♦  Théorème 1 - Image d'une droite :     

a/ Toute droite passant par O est globalement invariante par une inversion de pôle O.
b/ L'inverse d'une droite ne passant pas par le pôle d'inversion O est un cercle passant par O.

∗∗∗  On étudie la preuve de ce résultat en exercice.

Inversement, puisque l'inversion est involutive :

c) L'inverse d'un cercle (c) passant par le pôle O d'inversion est une droite

Inverseur de Peaucellier :  »

♦  Théorème 2 - Image d'un cercle passant par le pôle :       

L'inverse d'un cercle (c) passant par le pôle O d'inversion est la droite parallèle à la tangente à ce cercle au point O.

Preuve : selon la réciproque du théorème 1, l'inverse de (c) est ici une droite. Si M' est l'image de M, traçons la droite (OH) où H est diamétralement opposé à O. L'image H' de H vérifie OH.OH' = OM.OM' et ces quatre points sont cocycliques. Or ^HMM' est droit, il en est donc de même de ^HH'M' : la droite (H'M') inverse de (c) est donc bien parallèle à la tangente en O.
» Sans faire référence au théorème 1, on peut retrouver que (H'M') est l'inverse de (c) : pour tout point m de (c), traçons [Om] coupant  (H'M') en m'. L'angle ^OmH est droit. Par conséquent, les points m, H, H', m' sont sur un même cercle (γ) et la puissance de O par rapport à (γ) est Om.Om' =  OH.OH' : m' est l'image de m par notre inversion.

Le théorème 2 montre que l'inversion n'est donc pas une application affine (une telle application transformerait une droite en une droite), en voici une illustration où l'on se donne un segment [AB] et son milieu M :

Si votre navigateur accepte les applets Java (» extension CheerpJ) :
Vous pouvez déplacer O et déformer le triangle ABC en déplaçant les points A, B et C

∗∗∗
En suivant ce lien, on étudiera une reprise du résultat précédent en utilisant le fait qu'une inversion est involutive et que l'image d'une droite
ne passant pas par le pôle d'inversion O est un cercle passant par O.

♦  Théorème 3 :     

Dans une inversion transformant une droite (d) en un cercle (c), le centre de (c) et le symétrique du pôle par rapport à (d) sont inverses l'un de l'autre.

L'inversion étant involutive, il revient au même de dire :

Dans une inversion transformant un cercle (c) en une droite (d), le centre de (c) et le symétrique du pôle par rapport à (d) sont inverses l'un de l'autre.

Preuve : Selon le théorème 1b, (c) passe par le pôle d'inversion O. Soit C son centre, C' son inverse, k la puissance d'inversion, H la projection orthogonale de O sur (d). Son inverse est H' diamétralement opposé à O. On a OC.OC' = OH.OH' = k et OH' = 2OC, donc OC.OC' = 2 OH.OC, c'est à dire OC' = 2OH : C' est le symétrique de O par rapport à (d).

En application de ce résultat, la construction au seul compas du centre d'un cercle donné :  »

♦  Théorème 4 - Image d'un cercle ne passant pas par le pôle :       

L'inverse d'un cercle (c) ne passant pas par O, dans l'inversion de pôle O de puissance k, est un cercle, image de (c) dans l'homothétie de centre O, de rapport k/p, où p = P_/(c)(O) désigne la puissance de O par rapport au cercle (c).

Application à la construction au seul compas du centre d'un cercle donné :  »

Preuve : Ci-dessous, on a choisi M à l'extérieur du cercle d'inversion (cercle rouge). Traçons la droite (OM). Elle recoupe (c) en m. On a OM.Om = p, puissance de O par rapport à (c). Notons M' l'image de m dans l'homothétie h de rapport k/p, k désignant la puissance d'inversion de pôle O. On a OM' = k/p × Om,  d'où Om = p/k  × OM'. Par conséquent OM.OM' = k : M' est l'image de M dans l'inversion considérée. M' est donc élément de (c'), image de (c) par h. Inversement, à tout point M' de (c') correspond un unique m de (c) par h^-1 et, par suite un unique point M de (c).

♦  Théorème 4   

Un cercle orthogonal au cercle d'inversion est globalement invariant.   

Preuve : Soit M un point d'un cercle (c) orthogonal au cercle d'inversion (i) . (OM) recoupe (c) en M'. (c) et (i) étant orthogonaux, on a  OM.OM' = P_(c)(O) = r², r désignant le rayon du cercle d'inversion. Donc OM.OM' = (√k⁾² = k. C'est dire que M', point de (c), est l'image de M par l'inversion T considérée. L'image de (c) par T est donc incluse dans (c) et selon a/ on peut conclure que cette image est (c) lui-même.

♦  Conservation des angles :     

Soit une inversion T de pôle O, de rapport k > 0. Considérons l'angle formé par deux demi-droites [Mx) et [My), de sommet M n'appartenant pas au cercle d'inversion (de centre O, de rayon √k) . Soit M' l'image de M par l'inversion T. Considérons les deux cercles passant par M et M' admettant respectivement [Mx) et [My) comme tangente en M. Ils sont définis de façon unique par leurs centres respectifs C₁ et C₂ situés sur la médiatrice de [MM'] sous la condition ^xMC₁ = yMC₂ = 90°.

Eu égard à la relation OM.OM' = (√k)², ces cercles sont tous deux orthogonaux au cercle d'inversion. Selon le résultat précédent c/, ils sont donc globalement invariants par T. On est donc en situation de symétrie orthogonale : les tangentes en M' font le même angle qu'en M (d'orientation opposée).

♦  Image du pôle O par inversion, point à l'infini :     

Afin qu'une inversion T devienne une bijection du plan, on peut remarquer que si un point M s'approche infiniment près du pôle O, son image s'éloigne infiniment loin de O. Notons alors ∞ cette image : point à l'infini. Cela n'a de sens que si elle ne dépend pas de la direction de la demi droite [OM). Convenons donc de cette unicité. Cela revient à dire, topologiquement, que si M tend vers O, de quelque manière que ce soit, alors T(M) tend vers O : T devient alors un homéomorphisme (bijection continue), également appelé transformation topologique. L'inversion devient ainsi une transformation conforme (bijection conservant les angles) et le plan muni de ce point à l'infini est appelé plan conforme.

 »  Mercator Gerhard Kremer

♦  Quelques généralisations concernant l'inversion dans l'espace :     

• l'inverse d'un plan ne passant pas par le pôle O est une sphère passant par O.

• Inversement... : l'inverse d'une sphère passant par le pôle O est un plan perpendiculaire au diamètre passant par O.

• L'inverse d'une sphère ne passant pas par le pôle O est une sphère de centre C dont le centre est l'inverse du pied sur (OC) du plan polaire de O par rapport à C.

• Quel que soit le pôle, l'inverse d'un cercle est un cercle (car on peut toujours considérer ce cercle comme intersection de deux sphères ne passant pas par le pôle).

Le plan étant muni d'un repère orthonormé d'origine O, soit T une inversion de pôle O, de puissance k, qui à tout point M(x,y) autre que O, associe le point M'(x',y'). On a donc, par définition  :

OM . OM' = k

On montrera facilement que :

x' = kx/(x² + y²)  ,  y' = ky/(x² + y²)

On peut ainsi identifier l'inversion de pôle O, de puissance k à la transformation complexe :

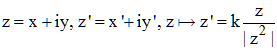
 !  Mais bien noter qu'il ne s'agit pas de z →z' = k/z, équivalente à :

composée de l'inversion (de pôle O, de puissance k) suivie la symétrie par rapport à (Ox), z →z : les images sont conjuguées. Cette transformation, z → k/z, composée de l'inversion complexe (z → 1/z) par l'homothétie de centre O de rapport k, ne conserve pas l'alignement.

∗∗∗
a) Inversion complexe (expr. analytique) et l'inversion géométrique : exercice corrigé
b) voir aussi l'étude de la transformation αzz' + βz + γz' + δ = 0 , α ≠ 0 : page Möbius

♦  Inversion dans l'espace :     

L'expression analytique donnée ci-dessus se généralise immédiatement à l'espace :

x' = kx/(x² + y² + z²)  ,  y' = ky/(x² + y² + z²) ,  z' = kz/(x² + y² + z²)

Projection stéréographique :  »

Des courbes ou des surfaces globalement invariantes par une inversion sont dites anallagmatiques (du grec α, αν =  a, an privatif, sans et allagma = changement).

• La strophoïde est une courbe anallagmatique : elle est globalement invariante dans une inversion dont le pôle est son sommet, de puissance son paramètre.

• Il en est de même des ovales de Cassini et, par là, de la lemniscate.

∗∗∗
Vérifier que l'inversion de pôle O, de puissance 1, transforme la strophoïde x(x² + y²) - a(y² - x²) = 0 en une hyperbole.

L'inversion intervient en géométrie projective et dans des démonstrations simples et élégantes de théorèmes a priori ardus comme celui de Feuerbach ou de Ptolémée.

♦  Théorème :

Toute courbe anallagmatique est l'enveloppe d'une famille de cercles (F) coupant orthogonalement un cercle fixe (φ), dit cercle directeur ou cercle d'inversion, et dont les centres décrivent une courbe fixe (Γ) dite directrice ou déférente.

Si O désigne le centre du cercle directeur (φ) de rayon r, la puissance de O par rapport à tous les cercles de (F) est constante et égale à r². Pour obtenir un cercle de la famille (F), on trace le cercle d'inversion (φ) de centre O. Soit M le centre d'un cercle de la famille F. On trace le cercle (γ) de diamètre [OM] coupant (φ) en A et B. Le cercle de centre M passant par A (et par B) est le cercle cherché :

Il n'y a plus qu'à en tracer un bon nombre... ou utiliser un logiciel, comme ci-dessous !

En traçant la tangente en M à l'hyperbole, la normale à cette tangente passant par O coupe le cercle orthogonal à (φ) en deux points de l'enveloppe. Voir, plus généralement :

Courbes cycliques :  »