ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 

Méthode des différences finies #2          » programme JavaScript  | » 1er ordre  y' = φ(x,y)      Méthode d'Euler pour la résolution approchée d'une EDO du 2nd ordre y'' = φ(x,y,y')

On s'intéresse ici à l'équation différentielle explicite du second ordre, d'inconnue y = f(x) définie sur l'intervalle J = [a,b] par :

y" = φ(x,y,y'), avec x_o , y_o , y'_o donnés, x ∈ [a,b]       (e)

Cas particulier des équations différentielles linéaires du second ordre : »

Revenons au cas général (e) : on transforme cette équation d'inconnue y = f(x) en un système de deux équations différentielles du 1er ordre en posant u = y' :

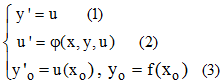
On recherche une solution approchée sous la forme d'un nuage de points (x_i, y_i), y_i = f(x_i) en subdivisant J en n sous-intervalles (de même amplitude pour simplifier l'algorithme) :

a = x_o  < x₁ < x₂ < ... < x_n= b , x_i = a + ih, h = (b - a)/n

• Semblablement au cas y' = f(x,y) du 1er ordre, une approximation de y'(x_i) est (y_i+1 - y_i )/(x_i+1 - y_i) = (y_i+1 - y_i )/h;

• Si u_i désigne l'approximation de u(x_i), on peut écrire, selon (1) : (y_i+1 - y_i )/h = u_i;

• Une approximation de u'(x_i) est (u_i+1 - u_i)/h devant égaler, selon (2), φ(x_i,y_i,u_i).

Les relations (1), (2) et (3) sont alors respectivement discrétisées en :

 ➔    Pour tester ce programme vous devez entrer votre fonction φ(x,y) en utilisant une syntaxe comprise par le langage JavaScript. L'instruction with (Math), placée en début de procédure, évite à l'utilisateur de préciser Math devant chaque fonction mathématique utilisée. Les opérations et fonctions usuelles sont les suivantes :

• multiplication : * ,   division : /
• racine carrée : sqrt(x)
• puissance : pow(x,n). Pour x² ou x³, utiliser plutôt x*x et x*x*x
• fonctions usuelles : sin(), cos(), tan(), atan(), abs();
• log népérien : log() , exponentielle de base e : exp() , ...
• les appellations pi (pour π) et e sont comprises par le programme.

On entrera y'' = φ(x,y,y') sous la forme d'une fonction de x, y, et u pour désigner y'.

Le programme utilise par défaut l'équation différentielle  x²y" + xy' + y = 0  sur [1,5/2] avec y(0) = 0, y'(0) = 1.
On peut écrire y" = (- xy' - y)/x²; on entrera donc (en utilisant la notation u pour y') : (-x*u - y)/(x*x). a = 1, b = 2.5, x_o = 0, y_o = 0, y'_o = u_o = 1. La solution exacte de ce cas particulier d'équation d'Euler est : y = sin(lnx).