équation du second degré

où a, b et c sont des nombres réels ou complexes donnés, a étant non nul. Le membre de gauche est un polynôme du second degré : c'est un trinôme (trois termes) du second degré.

Des résolutions partielles de cette équation apparaissent au fil des âges (en particulier avec Al-Khwarizmi et Abu Kamil au 9è/10è siècle, Savasorda au 11è siècle). La résolution complète apparaît chez Viète avec la présence de solutions négatives cependant considérées comme fausses ! Le statut de nombre pour une quantité négative sera pleinement reconnu grâce à Gauss.

➔ Le nombre Δ = b² - 4ac est appelé discriminant de l'équation (appellation due à Sylvester en 1851, du latin discrimen = séparation) : l'étude de son signe permet de conclure quant au nombre et aux valeurs des racines de l'équation.

♦ Δ < 0 : (x + b/2a)² est alors négatif; par suite il n'y a pas de solution.

♦ Δ = 0 : (x + b/2a)² est alors nul; il y a une solution

dite double car l'équation est équivalente à :

Notons x' et x'' les solutions de l'équation ax²+ bx + c = 0 lorsqu'elles existent. D'après (e) et (e') ci-dessus, on à l'égalité :

Ces formules, que l'on peut aussi obtenir directement à partir de (sol) ci-dessus, sont des fonctions symétriques des racines. Elles permettent de calculer deux nombres connaissant leur somme et leur produit.

∗∗∗

Pyramide de nombres #2 équation x² = A

Triangle égyptien triangle rectangle dont les côtés sont des entiers consécutifs

Triangle d'or propriété de la bissectrice d'un angle, nombre d'or

Calcul d'un angle #2 système non linéaire - sinus - théorème de Pythagore

Cadastre somme et produit des racines

Un problème massif somme et produit des racines

Problème de pommes équation du second degré

Rues Jeanne et Darc #2 équation du second degré

Trisection d'un terrain calcul d'aires, équation du second degré de la forme ax² = b

Taux d'intérêt calcul d'un taux se ramenant au second degré

Taux d'intérêt (bis) calcul d'un taux sur 18 mois (intérêts simples)

Résistances montage en parallèle (somme et produit des racines)

Bassin & allée équation du second degré

Jardinier & buissons système du second degré

Abreuvoir figures homothétiques & second degré

Croisement aérien second degré et formule d'Al Kashi

» Etude de fonctions trinômes

♦ Δ < 0 : on peut écrire Δ = i² × | Δ |, ce qui nous ramène au cas Δ > 0 précédent. On remarque alors que les solutions sont complexes conjuguées.

Il s'agit de rechercher les racines carrées de Δ, ce que l'on fait soit par une méthode trigonométrique, soit par une méthode algébrique. Si δ est une de ces racines, on a dans tous les cas :

∗∗∗
1. Résoudre l'équation 2x² + 6x + 5. Rép : x = -3/2 ± i/2
2. Résoudre l'équation x⁴ = x²- 1. Rép : on a x² = 1/2 ± i√3/2 = cosπ/3 ± i.sinπ/3 » forme trigonométrique
d'où x = ± (cosπ/6 + i.sinπ/6) ou x = ± (cos[-π/6] + i.sin[-π/6] ). Finalement : x = ±(√3/2 ± i/2)

» on a bien 4 solutions conformément au théorème de d'Alembert

En posant b' = b/2, le discriminant Δ = b² - 4ac peut s'écrire 4(b^'2 - ac); on pose alors traditionnellement Δ' = b^'2 - ac : discriminant réduit, et si δ' désigne une racine carrée de Δ' , on obtient une formule simplifiée :

♦ cas d'une résolution dans C : δ désignant une des racines carrées de Δ :

On rencontre par exemple ces inéquations dans l'étude du signe d'une fonction dérivée afin de déterminer le sens de variation d'une fonction :

∗∗∗
1. Résoudre dans R, l'inéquation -5x²+ 2x + 3 ≤ 0.
Rép : L'équation -5x²+ 2x + 3 = 0 possède deux solutions x = 1 et x = -3/5.
Le coefficient de x²est -5 < 0, par conséquent les solutions sont les réels de l'ensemble ]-∞,-3/5] ∪ [1,+∞[.

2. Résoudre dans R l'inéquation : x³ + x² - 6x < 0
Rép : On met x en facteur : x(x² + x - 6) < 0 et pour plus de clarté, on fait un petit tableau de signes :

Ces équations peuvent avoir diverses formes. On les résout facilement lorsqu'il est possible d'isoler les radicaux dans un memebre et en élevant au carré en posant les conditions d'équivalence. Par exemple :

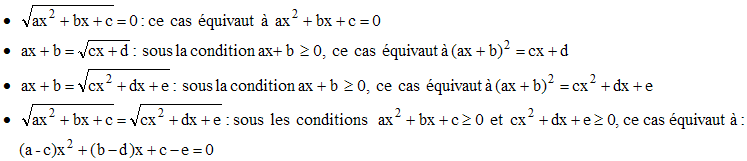
! Il s'agit de ne pas oublier de bien poser la (ou les) les condition(s) d'élévation au carré et de vérifier, après résolution, que les solutions trouvées conviennent.

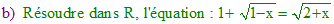
Rép a/ : on pose la condition 3x - 7 ≥ 0, soit x ≥ 7/3 ; on élève au carré (la positivité de x + 1 sera alors assurée) et on trouve x = 3 ou x = 16/9. Cette dernière solution est à rejeter car 7/3 = 21/9 > 16/9. Seul x = 1 est donc solution de l'équation.

Rép b/ : On pose les conditions 1 - x ≥ 0 et 2 + x ≥ 0, soit x ≤ 1 et x ≥ -2. On élève au carré, ce qui conduit à √(1 - x) = x. On élève encore au carré sous la condition x ≥ 0 : 1 - x = x². Cette équation du second degré fournit x = (-1 ± √5)/2. La condition x ≥ 0 élimine (-1 - √5)/2. La seconde possibilité (-1 + √5)/2 = (√5 - 1)/2 est acceptable : elle vérifie x ≤ 1 et bien sûr x ≥ -2 puisqu'elle est positive.

» On remarquera que les élévations au carré conduisent à respecter les conditions posées préalablement : la 1ère élévation au carré assure la positivité de 2 + x. La seconde élévation au carré assure la positivité de 1 - x. Mais mieux vaut poser les conditions plutôt que de les oublier...

∗∗∗
A titre d'exercice complémentaire sur les radicaux : vérifier que (-1 + √5)/2 est effectivement solution de b)
en remplaçant x par cette valeur dans l'équation initiale.

∗∗∗

La résolution est laissée au lecteur : la différence par rapport à l'exercice b est une condition supplémentaire : le membre de gauche doit aussi être positif !
Il y a là encore une unique solution : x = (-1 - √5)/2.

! Une solution rationnelle ne peut exister si le discriminant n'est pas lui-même un carré de rationnel : il ne s'agira alors que d'une approximation rationnelle des solutions.