
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Translations , rotations , symétrie centrale , symétrie axiale , symétrie glissée , réflexion , antirotation , vissage | » résumé Applications affines (étude générale) , similitudes affines , interprétation complexe des similitudes du plan |
On suppose ici connus les notions d'application linéaire, d'application affine et leurs propriétés élémentaires. On se place dans le plan ou l'espace euclidien affine ε muni d'un repère orthonormé d'origine O. L'espace vectoriel sous-jacent est noté E. La distance entre deux points A et B est notée d(A,B), la norme d'un vecteur u est notée ||u|| et si u = AB, on a ||u|| = d(A,B).
On appelle isométrie toute application de ε dans ε conservant les distances :
f : ε → ε est une isométrie ⇔def pour tous points A et B : d(A,B) = d(f(A),f(B))
➔ Afin de simplifier les écritures, dans toute la suite les notations primées comme A', B', u', v', ... désigneront, en l'absence d'ambiguïté, les images de A, B, u, v, ...par une application. Ci-dessus d(f(A),f(B)) s'écrira simplement d(A',B').
Théorème 1a :
Toute isométrie de
ε est une
bijection affine de ε dont l'endomorphisme
associé φ est une isométrie vectorielle,
c'est à dire
un automorphisme (endomorphisme bijectif) vérifiant pour tout u de E : ||u||
= ||φ(u)||
Rappel :
Munies de la loi de composition des applications, les isométries vectorielles de E constituent un groupe noté O(E), sous-groupe du groupe linéaire GL(E) des endomorphismes de E.
Le groupe orthogonal O(E) : »
Lemme :
l'isométrie vectorielle φ associée à l'isométrie f définie par φ(OM) = O'M' conserve le produit scalaire et transforme donc une base orthonormée en une base orthonormée.
Preuve : En effet, on a successivement :
Pour tout u de E, il existe M unique tel que u = OM, donc :
||φ(u)|| = ||φ(OM)|| = ||O'M'|| = ||OM|| = ||u|| » on voit que φ conserve la norme
||φ(u - v)|| = ||φ(OM - ON)|| = ||φ(MN)|| = ||MN|| = ||M'N'|| = ||O'N'- O'M'|| = ||φ(ON) - φ(OM)|| = ||φ(u) - φ(v)||
Ainsi ||u - v|| = ||φ(u - v)||. Or le carré de la norme est le carré scalaire, donc en passant au carré et en simplifiant :
u.v = φ(u).φ(v)
Preuve du théorème : plaçons-nous dans le plan : par linéarité cela ne restreindra pas la généralité. Soit (i,j) une base de E. Tout vecteur u s'écrit de façon unique x.i + y.j. Il nous faut montrer que φ(x.i + y.j) = x.φ(i) + y.φ(j).
Or : (φ(i),φ(j) est une base orthonormée et, par suite, il existe x' et y' uniques tels que φ(x.i + y.j) = φ(u) = x'.φ(i) + y'.φ(j). L'application φ conservant le produit scalaire, on a φ(u).φ(i) = u.i. Mais le produit scalaire de gauche est x' et celui de droite est x; de même y' = y : ce qu'il fallait démontrer.
Théorème 1b (corollaire) :
La matrice d'une isométrie vectorielle de E est une matrice orthogonale. On a donc M-1 = tM et det(M) = ± 1.
» Charles Hermite et les matrices orthogonales
Théorème 2a :
Muni de la loi de composition des
applications, l'ensemble des isométries f : ε→
ε est un groupe
noté Iso(ε),
sous-groupe du groupe GA(ε)
des bijections affines de ε.
Théorème 2b :
Soit A donné dans ε.
L'ensemble des isométries f : ε→
ε laissant A
invariant est un sous-groupe de Iso(ε)
isomorphe au groupe orthogonal O(E).
Preuves : fort simples, laissées au lecteur...
| Déplacements & antidéplacements des plans et espaces euclidiens : |
Une isométrie dont l'endomorphisme associé φ est une rotation vectorielle (isométrie positive det φ = +1) est qualifiée de déplacement : elle conserve non seulement les distances mais aussi les angles orientés. On parle encore de rotation (affine). L'identité s'identifie à une rotation d'angle nul.
A contrario, les antidéplacements, comme la symétrie par rapport à un plan, ont pour endomorphisme associé une isométrie négative (det φ = -1); elles changent les angles en leurs opposés.
Déterminant d'un endomorphisme : »
Eu égard à det (φ1 o φ2) = det φ1 x φ2, l'isométrie composée :
de deux déplacements ou de deux antidéplacements est un déplacement;
d'un déplacement et d'un antidéplacement est un antidéplacement.
| Liste des isométries du plan et de l'espace euclidiens : |
Généralités :
♦ Dans le plan, outre l'identité, les déplacements se résument aux rotations (unique point invariant : le centre de rotation) et aux translations (aucun point invariant).
Les antidéplacements sont constitués des symétries axiales (dont les points invariants sont leur axe) et des symétries glissées (aucun point invariant, composées d'une symétrie axiale et d'une translation).
Un antidéplacement du plan admettant au moins un point invariant est une symétrie axiale.
♦ Dans l'espace, outre l'identité, les déplacements se résument aux rotations (dont les points invariants constituent leur axe), aux translations (aucun point invariant) et aux vissages (aucun point invariant, composées d'une rotation et d'une translation).
Les antidéplacements sont constitués des réflexions (symétries orthogonales par rapport à un plan constituant leurs points invariants), des symétries glissées (aucun point invariant, composées d'une réflexion et d'une translation) et des antirotations (admettant un unique point invariant, composées d'une rotation et d'une réflexion).
La translation :
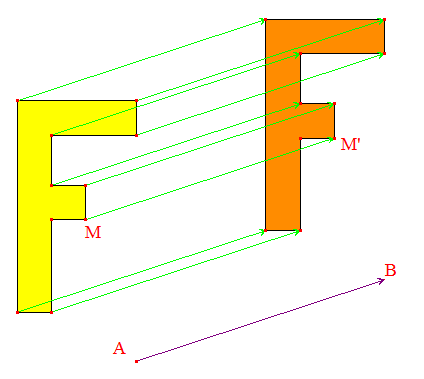
La translation de vecteur donné, comme celle de vecteur AB illustrée ci-dessous est l'isométrie la plus élémentaire. C'est un déplacement dont l'endomorphisme associé est l'identité id : v→v. Elle est étudiée sur la page dédiée aux applications affines :
La translation (exposé élémentaire) : »

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() )
:
)
:
Vous pouvez modifier le vecteur AB et déplacer certains points du
F jaune
dont l'image (le translaté) est le F
rouge.
Translation & addition vectorielle, composée de deux translations : »
La symétrie axiale :
On parle également de symétrie orthogonale par rapport à une droite. C'est une isométrie involutive. Dans le plan, c'est un antidéplacement; dans l'espace, c'est une rotation d'angle π, donc un déplacement.
Symétrie axiale (exposé élémentaire) : » Symétrie (oblique) par rapport à une droite : »
La réflexion :
On parle également de symétrie orthogonale par rapport à un plan P. C'est est une isométrie involutive dont l'ensemble des points invariants est P. Il s'agit d'un antidéplacement. Rapportée à une base (u,v,w) où (u,v) dirige P, la matrice de l'endomorphisme associé s'écrit :
La symétrie centrale :
Dans le plan, il s'agit d'une rotation d'angle π dont l'endomorphisme associé est -idE de déterminant +1. C'est donc un déplacement.
Symétrie centrale (exposé élémentaire) : »
Dans l'espace, la symétrie centrale par rapport à un point O, d'endomorphisme associé -idE de déterminant -1, est un antidéplacement. On démontre qu'on peut la décomposer d'une infinité de manières comme composée de trois symétries par rapport à des plans deux à deux perpendiculaires contenant O :
La symétrie glissée (ou symétrie-translation) :
Dans le plan (resp. l'espace), il s'agit d'un antidéplacement ne possédant aucun point invariant. Elle s'écrit de façon unique (décomposition canonique) comme composée commutative S o T = T o S d'une symétrie axiale (resp. par rapport à un plan) de direction δ et d'une translation T de vecteur appartenant à δ.
∗∗∗
e1) On considère un triangle (quelconque) ABC; soit A' le milieu de [BC], B' et C' les projetés orthogonaux de B et C sur (AA').
Prouver que le quadrilatère BB'CC' est un parallélogramme. BB'CC' peut-il être un losange, un rectangle ? ☼
e2) Prouver que toute isométrie du plan admettant au moins 2 points invariants est soit l'identité id : M → M, soit une symétrie axiale.
∗∗∗ symétrie glissée #1 | symétrie glissée #2
La rotation dans le plan (rotation plane) :
Le plan étant muni d'un repère orthonormé (O,i,j) et ayant fait le choix d'une orientation, on appelle rotation de centre A, d'angle â, l'application du plan qui à tout point M fait correspondre M' tel que ^(AM, AM') = â.
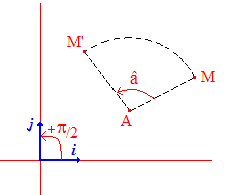
Il s'agit d'une isométrie; c'est un
déplacement du plan.
➔ Rappelons ici brièvement que par orientation, on entend que l'on a choisi un sens de rotation positif : c'est celui qui amène i en j par une rotation d'un quart de tour autour de l'origine. Généralement, c'est le sens inverse des aiguilles d'une montre : le célèbre sens trigonométrique... Dans ces conditions, on peut parler d'un angle de 30° ou de - 30°, ou en radians, d'un angle de π/6 ou -π/6. On parle aussi d'angle orienté de vecteurs :
^(i, j) = + π/2 , ^(j, i) = - π/2
L'endomorphisme associé est une rotation vectorielle du plan. Lorsque â n'est pas nul, le centre A de la rotation est le seul point invariant.
Théorème 3 :
Dans le plan euclidien orienté les
composées R o S et S o R d'une rotation de centre A et d'une symétrie axiale
S d'axe
passant par A sont des symétries axiales d'axe contenant A
preuve : S o R et R o S, composées d'un déplacement et d'un antidéplacement du plan sont des antidéplacements. (S o R)(A) = S(A) = A : S o R est un antidéplacement du plan admettant au moins un point invariant. C'est une symétrie axiale. De même pour R o S.
Antirotation : »
∗∗∗
Dans le plan euclidien orienté rapporté à un repère orthonormé (O, i, j), on considère la rotation de centre O, d'angle π/4
et la symétrie axiale S d'axe (O, i). préciser les éléments caractéristiques de S o R et R o S ☼
Théorème 4 :
Tout déplacement du plan est la composée de deux symétries orthogonales dont l'une est arbitraire
Exemples illustrés : »
La rotation dans l'espace :
On parle de rotation d'angle â et d'axe δ, ou autour de δ, pour signifier que l'image M' de tout point M s'obtient par rotation plane dans le plan perpendiculaire à δ contenant M.
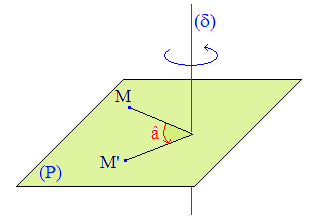
La droite δ est l'ensemble des points invariants et l'endomorphisme associé est une rotation vectorielle de l'espace.
Théorème 5 :
Toute rotation d'axe δ, d'angle â, peut se décomposer en un produit de deux réflexions dont les plans s'intersectent en δ. Si α désigne leur angle dièdre (modulo π), on a 2α = â.
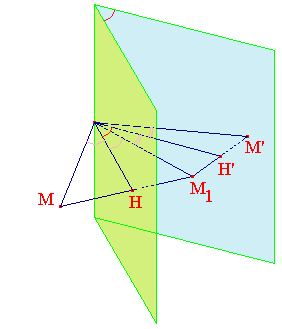
➔ Remarquer que dans l'espace, la symétrie axiale (symétrie orthogonale par rapport à une droite) est un déplacement : rotation d'angle π autour de l'axe δ. On parle de demi-tour ou de retournement.
∗∗∗
Une application élégante des rotations | Théorème de Van Aubel
Carré au milieu... | C'est bien évident ! | Autre application des rotations
Le vissage :
Aussi appelé déplacement hélicoïdal, le vissage est une isométrie affine de l'espace sans point invariant dont l'endomorphisme associé est une rotation vectorielle.
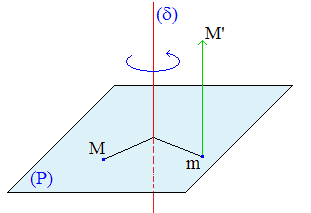
On démontre qu'elle peut s'écrire comme la composée commutative (décomposition canonique) R o T = T o R d'une rotation d'axe δ et d'une translation dont le vecteur a même direction que δ.
On voit là le lien avec la vis ou le tire-bouchon et, plus mathématiquement, avec l'hélice circulaire.
∗∗∗ décomposition canonique d'un vissage
L'antirotation :
On nomme parfois ainsi l'isométrie, composé commutatif R o S = S o R d'une rotation R d'axe δ et de la symétrie S (réflexion) par rapport à un plan P orthogonal à δ. Il s'agit donc d'un antidéplacement. Une telle isométrie admet un unique point invariant O, intersection de P et δ.
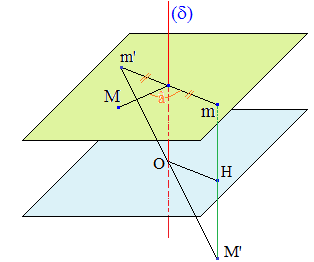
∗∗∗
Avec les notations ci-dessus, montrer par des considérations géométriques
élémentaires, que l'antirotation s'interprète comme le composé
commutatif
de la rotation d'angle â + π (ou de R suivie du demi-tour d'axe
δ) et de la symétrie centrale par rapport à O.
Théorème 6 :
Les déplacements de l'espace, constitués
des translations, des rotations, des vissages et de l'identité forment
un
sous-groupe
du groupe Iso(ε) des isométries
de l'espace.
| Résumé des types d'isométries par classification selon leur ensemble de points invariants : |
| points invariants | déplacement | antidéplacement | |
| aucun |
|
|
|
| plan | un point |
|
|
| une droite |
|
|
|
| le plan |
|
|
|
| aucun |
|
|
|
| espace | un point |
|
|
| une droite |
|
|
|
| un plan |
|
|
|
| l'espace |
|
| Groupe de symétrie : |
Dans un espace affine euclidien E, considérons une figure F. On appelle groupe de symétrie de F, le sous-groupe des isométries de E laissant F globalement invariante. Ce groupe joue un rôle important dans l'étude des pavages du plan et de l'espace, ainsi qu'en cristallographie.
» Klein et les groupes de transformations , Coxeter et groupe diédral
1.
Vissage : Dans l'espace euclidien usuel εde dimension 3 rapporté au repère orthonormé (O,i,j,k), on considère la transformation f qui à tout point M(x,y,z) de l'espace associe le point M'(x',y',z') défini par :x' = - y + 1 , y' = x + 1 , z' = z + 1
a/ Montrer que que l'endomorphisme φ associé à f est une rotation vectorielle d'angle +π/2.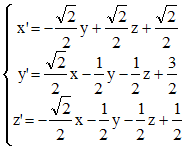
On note S la symétrie orthogonale par rapport au plan (P) d'équation y + z = 1. Montrer que f = S o R, où R est une rotation dont on précisera l'axe.