ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
Loi binomiale 
     @ Calcul des Prob (B = k) : programme JavaScript | loi des grands nombres | Loi multinomiale

Dans son Ars conjectandi (1713), Jacques (Jakob) Bernoulli définit la variable aléatoire qui porte son nom : une épreuve de Bernoulli est une expérience aléatoire conduisant à deux éventualités : l'une appelée succès de probabilité p, à laquelle nous associons la valeur 1; l'autre appelée échec de probabilité q = 1 - p, à laquelle nous associons la valeur 0.

On peut définir alors une variable aléatoire discrète X à valeurs dans {0,1}, dite de Bernoulli dont la loi de probabilité se réduit à

Prob{X = 1) = p et Prob{X = 0} = q

Répétons n fois une même épreuve de Bernoulli et notons Xi la variable aléatoire associée à la i-ème expérience. Les lois des Xi sont identiques et on a encore Prob{X = 1) = p et Prob{X = 0} = q. En posant :

B = X1 + X2 + ... + Xn

Bernoulli invente (découvre) la loi binomiale, souvent notée B(n,p) : il y a Cnk façons (nombre de combinaisons de k objets parmi n.) d'obtenir k succès au cours des n expériences et chacune d'elles a la même probabilité de réalisation, à savoir pkqn-k car les Xi sont des variables indépendantes : P(Xi/Xj) = P(Xi).

Finalement :

Prob{B = k} = Cnk x pkqn-k      (pbk) 

L'appellation binomiale est due au lien avec le développement de la formule du binôme de Newton, fournissant (a + b)n : remarquer que la somme des probabilités pour k variant de 0 à n doit être égale à 1; or p + q = 1 et, précisément, selon la célèbre formule :

 (p + q)n = Cno pnqo + Cn1 pn-1q1 + Cn2 pn-2q2 + ... + Cnn-1pqn-1 + Cnn poqn

 ➔  L'espérance mathématique, valeur moyenne d'une loi binomiale B(n,p) est np. Sa variance est npq.

Notion d'espérance mathématique, variance, écart-type : »

Somme de deux variables binomiales :    

Noter que si X et Y sont des variables aléatoires indépendantes suivant toutes deux une loi binomiale de paramètres respectifs (n1,p) et (n2,p), alors X + Y suit une loi binomiale de paramètres (n1 + n2, p).

∗∗∗
 1. On suppose que les probabilités de naissance d'une fille ou d'un garçon sont les mêmes (en fait, un peu plus de garçons : 52%) et qu'il y a indépendance des sexes d'une naissance à l'autre. Dans une famille de quatre enfants, quelle est la probabilité qu'il y ait deux filles et deux garçons ?  ☼

2. Vérifier par un calcul simple au moyen de l'égalité (pbk) ci-dessus ou par récurrence que :


           ∗∗∗
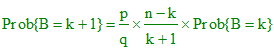
Y a-t-il vraiment plus de garçons que de filles ? (loi du khi2) , fille ou garçon ?

          Loi normale (Laplace-Gauss) en tant que "limite" de la loi binomiale :  »

                              

 »  De Moivre , Poisson , Gauss

Lois des grands nombres (Bernoulli, Poisson) : »             Loi fortes des grands nombres (Borel, Kolmogorov) : »

Loi multinomiale

La loi binomiale, étudiée ci-dessus, se généralise à une variable aléatoire X pouvant prendre k valeurs distinctes qualitatives ou quantitatives (au lieu de 2) avec les probabilités associées p1, p2, ..., pk (on parle parfois d'alternative généralisée). On répète n épreuves indépendantes et on s'intéresse au nombre d'apparition des événements [Xi = ni], i = 1, 2, ..., k avec n1 + n2 + ...+ nk = n. La probabilité de l'événement ∩[Xi = ni] s'écrit :

 ➔  Par épreuves indépendantes, on doit entendre que les épreuves successives sont indépendantes en probabilité. Par exemple, en cas de tirage de boules dans une urne, il y a remise de la boule tirée avant répétition de l'épreuve.

∗∗∗
Une une contient 10 boules dont 4 rouges, 3 noires, 2 vertes et 1 blanche.
a) On tire au hasard, successivement avec remise, 5 boules. En utilisant la loi multinomiale, quelle est la probabilité d'obtenir 2 rouges, 2 noires et 1 verte ?
b) Retrouver cette probabilité en utilisant un raisonnement élémentaire du type "cas favorables/cas possibles".
c) Que devient la probabilité si le tirage est successif sans remise ?
d) Que devient la probabilité si le tirage des 5 boules est simultané ? ☼

© Serge Mehl - www.chronomath.com