
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Muni des lois quotients induites par Z dans les classes résiduelles modulo n, l'ensemble Z/nZ est un anneau commutatif. La classe d'un entier x de Z sera notée ici x'. Par définition, nous avons :
x' + y' = (x + y)' et x'y' = (xy)'
Voici les "tables de Pythagore" de Z/3Z qui est un corps car 3 est premier : » anneaux Z/nZ.
1' + 2' = 3', classe de 3, c'est à dire 0'.
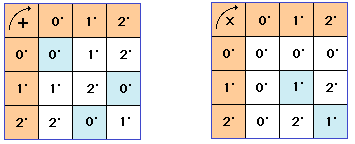
On établit facilement de même les
table
de Pythagore de l'addition et de la multiplication
dans Z/4Z :


On voit que la multiplication possède un diviseur de zéro : le produit de deux éléments non nuls peut être nul. C'est le cas de 2' dont le "carré" est nul. On note que 1' et de 3' sont leur propre inverse (pour 1' on s'y attendait...). 2' n'a pas d'inverse : il en est ainsi, dans un anneau, de tout diviseur de zéro.
∗∗∗
Exercice dans Z/6Z : déterminer les entiers
naturels n tels que n2 + 2 soit divisible par
6
☼
|
Z/4Z et les groupes finis d'ordre 4 : |
Le mathématicien allemand Felix Klein a montré qu'il n'y a, à un isomorphisme près, que deux groupes finis d'ordre 4. Rappelons qu'un isomorphisme de groupe est une bijection f entre deux groupes (G,*) et (H,$) respectant (ainsi que sa réciproque) les opérations de chacun, en ce sens :
➔ On connaît le groupe cyclique des puissances de i, célèbre nombre complexe dont le carré est -1 :
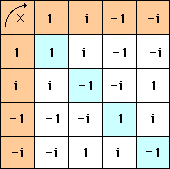
On peut facilement vérifier que ce groupe est isomorphe à Z/4Z en posant, pour toute classe x' de ce groupe :
f est surjective : f(0') = io = 1, f(1') = i1 = i, f(2') = i2 = -1 et f(3') = i3 = -i;
f est injective : si ix = iy , alors ix - y = 1; donc x - y = 4k, k entier relatif; et par suite x est congru à y modulo 4, donc x' = y';
f respecte les lois de groupe : f(x' + y') = ix' + y' = ix' × iy' = f(x') × f(y').
Cas du groupe diédral Dn lorsque n = 2 : »