ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

BAYES Thomas, anglais, 1702-1761

Théologien (protestant), il s'adonna aux mathématiques sous la houlette d'Abraham de Moivre en s'intéressant aux travaux de son maître : le calcul des probabilités et le calcul différentiel au sujet desquels il soutint et exposa la théorie newtonienne des fluxions (Introduction to the doctrine of fluxions, 1736), similaires, sur le continent, aux premières ébauches du calcul infinitésimal et au concept de fonction dérivée initiées par Leibniz. Introduit par De Moivre, ll fut élu membre de la Royal Society en 1742.

Bayes sera le premier, avant Laplace, dont il admira les travaux en ce domaine, à exposer, à titre posthume cependant car publié deux ans après sa mort (1763), un essai novateur en théorie des probabilités : Essay towards solving a problem in the doctrine of chances (essai sur la résolution d'un problème en théorie des probabilités). Contestées par Boole, mais aussi par Laplace dans ses premiers travaux en calcul des probabilités, les idées de Bayes ne se sont imposées que 20 ans après sa mort.

Avant d'aborder le théorème de Bayes, on rappelle ci-dessous les définitions, notations et résultats relatifs à l'indépendance en probabilité dont l'initiateur fut de Moivre :

En notations modernes, celles de Kolmogorov et de la théorie des ensembles, considérons un espace probabilisé (Ω, p) et soit A un événement de probabilité non nulle. L'application p_A, définie pour tout événement B de Ω par :

est une probabilité sur Ω, dite des probabilités composées. Le réel p_A(B) est la probabilité de réalisation de B sachant que A est réalisé; on parle de probabilité conditionnelle et on préfère souvent utiliser la notation p(B/A) : probabilité conditionnelle de B sachant A réalisé.

On a donc en général (résultat énoncé par de Moivre en 1718) : p(A∩B) = p(A) x p(B/A)  et comme A∩B = B∩A :

p(A∩B) = p(A) x p(B/A) = p(B) x p(A/B)

Si on note respectivement A et B les événements contraires de A et de B, on schématise souvent une situation probabiliste par un "arbre" comme :

    ou bien :

et on porte sur les branches les probabilités de l'événement auxquelles elles aboutissent, ce qui facilite la résolution d'un problème : 

♦ La somme des probabilités issues d'un même événement est égale à 1 : 

p(B/A) + p(B/A) = 1

♦En suivant une branche, on obtient la conjonction de deux événements, par exemple dans le cas ci-contre  :

p(A∩B) = p(A) × p(B/A) = 1/3 × 3/4 = 1/4

Cela signifie que la probabilité de la réalisation simultanée des événements A et nonB est 0,25.

La probabilité de l'événement A est 1/3; celle de B se calcule ainsi : on voit sur l'arbre que B peut se réaliser de deux façons, sachant que A a eu lieu ou non. Donc :

p(B) = p(A∩B) + p(A∩B)

Techniquement :

• On fait la somme des probabilités de chaque branche aboutissant à B.

• La probabilité d'une branche est le produit des probabilités rencontrés sur la branche.

 ➔  On peut retrouver ce résultat sur un schéma ensembliste où l'on voit que l'événement B est la réunion des deux événements incompatibles A∩B et A∩B :

Ainsi :

p(B) = p(A) x p(B/A) + p(A) x p(B/A) = 1/12 + 4/9 = 19/36.

∗∗∗   Extrait bac 2006, série S :

Dans une population donnée, la probabilité pour un individu d'être atteint d'une maladie M est de 0,003.
On réalise, dans cette population, un test de dépistage de la maladie :
si un individu est atteint par la maladie, le test n'est positif que dans 50% des cas et le test s'avère positif pour 3% des individus non touchés par la maladie.
Quelle est la probabilité d'avoir la maladie M lorsque le test est positif ?  Rép : ☼

♦  Événements indépendants :      

On dit que les événements A et B sont indépendants si p_A(B) = p(B) : la réalisation de A n'influence pas celle de B. C'est aussi dire que p_B(A) = p(A) ou encore que :

p(A∩B) = p(A) x p(B)

Or, p(B) = p(A∩B) + p(A∩B) et vu que 1 - p(A) = p(A), on obtient  p_A(B) = p(B). En définitive, et concrètement, B ne dépend aucunement de la réalisation ou non de A. Ce qui justifie pleinement cette notion d'indépendance en probabilité.

∗∗∗
Prouver que si A et B sont indépendants, il en est de même de A et B,  A et B,  A et B

 ➔  La situation se généralise à un nombre fini d' événements A₁, A₂, ..., A_n sont dits deux à deux indépendants si pour tout i et j distincts :

p(A_i∩A_j) = p(A_i) x p(A_j).

Plus généralement, on parle de famille d'événements indépendants {A₁, A₂, ..., A_n} (ou mutuellement indépendants) pour exprimer que :

Prob(A₁∩A₂ ∩...∩A_n) = Prob(A₁) × Prob(A₂) × ... × Prob(A_n)

Dans le cas d'une suite infinie A₁, A₂, ..., A_n, ... d'événements, on utilise le même vocabulaire pour signifier que tout famille finie extraite {A_i1, A_i2, ..., A_ip} de ces événements constitue une famille d'événements indépendants.

♦  Tribus et indépendance de variables aléatoires :       

On définit de même l'indépendance en probabilité de variables aléatoires par l'indépendance des événements qu'elles engendrent. Dans le cas de d'un couple (X,Y) de variables aléatoires discrètes, les variables X et Y sont indépendantes en probabilité lorsque, pour toutes éventualités (X = x_i ) et (Y = y_j), on a :

p[(X = x_i )∩(Y = y_j)] = p(X = x_i) × prob(Y = y_j)

En termes de probabilités conditionnelles : p[(Y = y_j)/(X = x_i)] = p(Y = y_j)  et  p[(X = x_i)/(Y = y_j)/] = p(X = x_i).

Plus généralement, dans le cadre du concept de tribu d'événements : Si X est une variable aléatoire à valeurs dans K, définie dans un espace probabilisé Ω et si J ⊂K, on vérifie facilement que les sous-ensembles {ω∈Ω / X(ω) ∈J} constituent une sous-tribu d'événements : on parle de tribu engendrée par X et on dit que les variables aléatoires X₁, X₂, ..., X_n sont indépendantes pour exprimer que les tribus engendrées par ces variables constituent des familles d'événements indépendants.

»  Kolmogorov , Markov         Cas d'un couple statistique :  » 

Dans la continuation des travaux de son maître, Abraham de Moivre, qui avait défini le nouveau concept d'indépendance en probabilités (Doctrine of Chances, 1718), Thomas Bayes expose, dans son traité de 1763, l'important problème de la probabilité des causes, à savoir l'estimation de la probabilité d'un événement complexe dont on sait que l'un (au moins) de ses composants, responsable de sa réalisation (une de ses causes) a eu lieu.

Soit A un événement conséquence a priori d'événements C₁, C₂, ..., C_n (causes). Avec les notations rappelées précédemment, la formule de Bayes, dite aussi des probabilités des causes peut s'écrire :

∗∗∗ Exemple : 

Des pièces usinées sont traitées par l'une ou l'autre des deux machines M₁ et M₂ d'une unité de production. M₁ et M₂ fournissent respectivement 60% et 40% de la production. Les statistiques d'échantillonnage permettent d'estimer respectivement à 2 et 3 pour 1000 les proportions de pièces jugées défectueuses produites respectivement par M₁ et M2.

Quelle est la probabilité qu'une pièce ainsi jugée provienne de M₂ ?

Réponse : Appelons D l'événement "une pièce est défectueuse". Nous cherchons à calculer la probabilité p(M₂/D), soit :

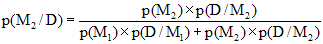
Ce qui nous donne : p(M₂/D) = 3/1000 x 0,4 / (2/1000 × 0,6 + 3/1000 x 0,4) = 0,5. On a donc 1 chance sur 2 qu'une pièce jugée défectueuse provienne de M2.

---

Daniel Bernoulli   Cramer

---

© Serge Mehl - www.chronomath.com