
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Facteur intégrant | Intégrale curviligne dans le champ complexe | Intégrale curviligne et longueur d'un arc |
➔ Pour la bonne compréhension de cette page, il faut connaître la notion de différentielle d'une fonction d'une ou plusieurs variables. On se restreint ici au cas de fonctions numériques d'une ou deux variables réelles, la généralisation à 3 variables ou plus est aisée.
Une écriture de la forme ω = ΣΦidxi où les Φi sont des fonctions continues des variables x1, x2, ..., xn sur un ouvert de Rn, est appelée forme différentielle ou encore forme de Pfaff du nom du mathématicien allemand J. F. Pfaff qui étudia ce sujet Elle est dite exacte ou immédiatement intégrable s'il existe une fonction f des variables x1, x2, ..., xn telle que ω soit la différentielle de f : ω = df. On doit écrire plus précisément :
ω(x1, x2, ..., xn) = Φ1(x1, x2, ..., xn)dx1 + Φ2(x1, x2, ..., xn)dx2 + ... + Φn(x1, x2, ..., xn)dxn
pour tout (x1, x2, ..., xn) d'un pavé U1 × U2 × ... × Un ouvert de Rn.
Cas d'une variable :
ω = P1dx1. Autrement écrit, ω = P(x)dx et P est la fonction dérivée de f. P étant continue sur l'intervalle d'étude qui sera ici un intervalle J = [xo,x] de l'ouvert U1, on est en droit d'écrire :

Dans le cas d'une variable, toute écriture de la forme P(x)dx est une différentielle exacte
Cas de deux variables (ou plus) :
Dans le cas de deux variables, ω = P1dx1 + P2dx2. Autrement dit, et plus précisément écrit, en posant x1 = x, et x2 = y, ω est de la forme (notation usuellement rencontrée) :
ω = P(x,y)dx + Q(x,y)dy
L'expression ω est ici définie dans un pavé U1 × U2 de R2. Plaçons-nous dans le plan euclidien orienté d'origine O :
Soit Γ une courbe plane; un point M(x,y) parcourt un arc continu AB, orienté de A vers B, (x,y) ∈ I × J, intervalles de U1 × U2.
On suppose que l'on peut écrire y = f(x)
avec f continue et strictement monotone sur I = [a,b]. Dans ces conditions, f est bijective de I
sur J = [f(a),f(b)] et il existe g : J
→ I telle que
x = g(y).
» si
f(b) < f(a)], avec les conventions usuelles, J deviendrait [f(b),f(a)].
Dans ces conditions :
i/ Le nombre :

est l'intégrale curviligne de P le long de l'arc AB.
ii/ Le nombre :

est l'intégrale curviligne de Q le long de l'arc AB. La somme de ces deux intégrales est encore dite curviligne, on la notera ici :

On peut donner un sens à une intégrale curviligne le long d'un arc AB non représentatif d'une fonction strictement monotone à condition de pouvoir décomposer l'arc AB par morceaux sur lesquels f est strictement monotone. On calcule l'intégrale curviligne par sommation des intégrales sur chaque morceau.
Si ω s'avère être la différentielle totale d'une fonction f : M(x,y) → f(x,y)∈R, on parle alors de forme différentielle exacte et on dit que ω est immédiatement intégrable en ce sens que :

C'est dire que le résultat ne dépend pas de l'arc AB utilisé : physiquement parlant, seuls nous intéressent les états initial et final.
Intégrale curviligne et longueur d'un arc : » Intégrale complexe et intégrale curviligne : » Théorème des résidus : »
! Rappelons qu'une forme différentielle P(x,y)dx + Q(x,y)dy n'est pas nécessairement exacte, ce serait trop beau... Rappelons deux résultats fondamentaux :
Théorème 1 :
Sur un ouvert connexe U de R2, la forme différentielle ω = P(x,y)dx + Q(x,y)dy est la différentielle totale d'une fonction (x,y) → f(x,y) et s'avère donc être une forme différentielle exacte si et seulement si P et Q sont continues sur U et admettent des dérivées partielles continues du premier ordre telles que :
 » différentielle
d'une fonction de plusieurs variables , connexité
» différentielle
d'une fonction de plusieurs variables , connexité
On a alors :

et ces égalités permettent de définir f à une constante additive près. On voit là que f admet des dérivées mixtes égales : ∂2f/∂x∂y = ∂2f/∂y∂x conforme au théorème de Schwarz.
∗∗∗ Un exemple élémentaire de forme différentielle exacte est donné par ω = ydx + xdy. Si f est la fonction recherchée, on doit avoir ∂f/∂x = P(x,y) = y et ∂f/∂y = Q(x,y) = x. On a bien ici ∂P/∂y = ∂Q/∂x. En intégrant la première équation, on obtient f(x,y) = xy + φ(y) : la "constante" d'intégration dépend a priori de y ! En dérivant par rapport à y, on est amené à : ∂f/∂y = x + φ'(y) = x pour tout (x,y). Finalement φ'(y) = 0 et f(x,y) = xy + k, k ∈ R.
Théorème 2 :
Sur un ouvert connexe U de R3, la forme différentielle ω = P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz est la différentielle totale d'une fonction (x,y,z) → f(x,y,z) et s'avère donc être une forme différentielle exacte si et seulement si P, Q et R sont continues sur U et admettent des dérivées partielles continues du premier ordre telles que :
 » différentielle
d'une fonction de plusieurs variables , connexité
» différentielle
d'une fonction de plusieurs variables , connexité
On a alors :
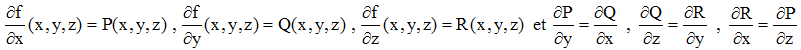
et ces égalités permettent de définir f à une constante additive près.
» Noter qu'en termes de champ vectoriel V(P,Q,R) on peut exprimer que V est le gradient de f, et que son rotationnel est nul. On dit que V dérive d'un potentiel scalaire, à savoir f(x,y,z). Voir le théorème 5.
∗∗∗
Vérifier que l'équation ω = ydx + xdy - xydz n'est pas exacte. On peut cependant
intégrer ydx + xdy - xydz = 0.
»
exercice in fine
Plus généralement :
Sur un ouvert connexe U de Rn, la forme différentielle ω(x1, x2, ..., xn) = ΣΦi(x1, x2, ..., xn)dxi sera la différentielle totale d'une fonction (x1, x2, ..., xn) → f(x1, x2, ..., xn) à valeurs dans R ssi ∂Φi/∂xj = ∂Φj/∂xi pour tout i distinct de j. On a alors pour tout i = 1, 2, ..., n : Φi = ∂f/∂xi.
∗∗∗ Considérons la forme différentielle ω = (2x + y)dx + (x - 2y)dy + 2zdz. Si f est la fonction recherchée, on doit avoir ∂f/∂x = P(x,y,z) = 2x + y, ∂f/∂y = Q(x,y,z) = x - 2y et ∂f/∂z = Q(x,y,z) = 2z. On vérifie facilement en calculant les six dérivées partielles relatives à P, Q et R, que les conditions du théorème 2 sont vérifiées. En intégrant la première équation, on obtient f(x,y) = x2 + xy + φ(y,z) : la "constante" d'intégration dépend a priori de y et z ! En dérivant par rapport à y, on est amené à : ∂f/∂y = x + φ'y = x - 2y pour tout (x,y,z). D'où φ'y = -2y et φ(y,z) = -y2 + ψ(x,z). Par suite : f(x,y,z) = x2 - y2 + xy + ψ(x,z). Ce qui conduit à ∂f/∂z = 2z = ψ'z. Finalement : f(x,y,z) = x2 - y2 + z2 + xy + k, k∈R.
Un vocabulaire pratique :
Ces théorèmes se généralisent à toute dimension n > 3. Les égalités relatives aux dérivées partielles des théorèmes 2 et 3 s'expriment en parlant de l'égalité des dérivées croisées (on retrouve les dérivées partielles ∂P/∂x, ∂Q/∂y (et ∂R/∂z dans le cas n = 3) en lisant les égalités en "croix". Une forme différentielle vérifiant l'égalité des dérivées croisées est dite fermée.
 Une partie
U (ouverte ou non) de
Rn est dite
étoilée lorsque U contient au moins un point A tel que pour tout
point B de U le segment [AB] soit inclus dans U. On dira aussi que U est étoilée
par rapport à A. On remarquera que la partie U est
convexe si et seulement si elle est étoilée par
rapport à chacun
de ses points. Toute partie étoilée est
connexe par arcs.
Une partie
U (ouverte ou non) de
Rn est dite
étoilée lorsque U contient au moins un point A tel que pour tout
point B de U le segment [AB] soit inclus dans U. On dira aussi que U est étoilée
par rapport à A. On remarquera que la partie U est
convexe si et seulement si elle est étoilée par
rapport à chacun
de ses points. Toute partie étoilée est
connexe par arcs.
Théorème 3 (théorème de Poincaré) :
Toute forme différentielle fermée sur un ouvert étoilé de Rn est exacte
Théorème 4 :
Soit ω est une forme différentielle de classe C1 sur un ouvert U de R2 ou R3. ω est une différentielle exacte si et seulement si l'intégrale curviligne :
∫Γ ω
est nulle pour toute courbe Γ fermée dans U.
∗∗∗
Voici un exemple certes assez trivial, mais apportant une illustration simple d'une
forme différentielle qui n'est pas une différentielle exacte : on considère,
dans le plan euclidien orienté, la forme ω = xdy - ydx.
Intégrer cette forme
lorsque Γ est le cercle unité parcouru dans le sens direct. On pourra
chercher à intégrer ω lorsque Γ est le
carré de côté 2, centré en O, de côtés parallèles aux axes parcouru également
dans le sens direct.

On peut aussi montrer que ω = xdy - ydx n'est pas une différentielle exacte au moyen du théorème 1. S'il en était autrement, on aurait ∂f/∂x = -y et ∂f/∂y = x. En intégrant la première équation (par rapport à x), on obtient f(x,y) = -xy + C(y) : la constante d'intégration ne dépend que de y. Mais cela est incompatible avec ∂f/∂y = x. On pourrait aussi invoquer les dérivées croisées en constatant que ∂2f/∂x∂y = -1 ≠ ∂2f/∂y∂x = 1.
Théorème 5 :
Soit Γ un arc de courbe AB inclus dans un ouvert U connexe de Rn (n = 2 ou n = 3, plan ou espace euclidien orienté) admettant une représentation paramétrique (r) :
t → (x(t), y(t)), n = 2 • t → (x(t), y(t), z(t)), n =3
t décrivant l'intervalle [a,b], l'origine A de Γest l'image de a par (r), l'extrémité B est l'image de b. On suppose en outre que ces représentations sont de classe C1 (continûment différentiables) sur U. Dans ces conditions, considérons une forme différentielle continue sur U :
ω = P(x,y,z)dx + Q(x,y,z)dy , n = 2 • ω = P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz , n = 3
On a dx = x'(t)dt, dy = y'(t)dt et dz = z'(t)dt et cet important résultat :
ne dépendent pas de la représentation paramétrique choisie et sont notées tout simplement :

De plus, lorsque V(P,Q,R) est le gradient d'une fonction f (» théorème 4), c'est à dire :
 ,
,
la seconde intégrale n'est autre que celle de df/dt, dérivée de t → f(x(t),y(t),z(t)) par rapport à t, et conduit alors à f(B) - f(A).
➔ En sciences physiques, l'intégrale de ω, intégrale du gradient de f, s'interprète comme une différence ce potentiel. En particulier, les surfaces de niveau, d'équation f = cte, prennent le nom de surfaces équipotentielles.
 Dans ce contexte, on
peut interpréter les intégrales (i)
comme celle du produit scalaire <V,T
> où V
désigne le vecteur de coordonnées (P,Q) dans le plan et (P,Q,R) dans le cas de l'espace et
T le vecteur tangent à la courbe de
coordonnées (x'(t),y'(t)) dans le plan, (x'(t),y'(t),z'(t)) dans le cas de l'espace.
Dans ce contexte, on
peut interpréter les intégrales (i)
comme celle du produit scalaire <V,T
> où V
désigne le vecteur de coordonnées (P,Q) dans le plan et (P,Q,R) dans le cas de l'espace et
T le vecteur tangent à la courbe de
coordonnées (x'(t),y'(t)) dans le plan, (x'(t),y'(t),z'(t)) dans le cas de l'espace.
Dans l'espace, en faisant appel à l'abscisse curviligne, on peut écrire :
w = (X.dx/ds + Y.dy/ds + Z.dz/ds) × ds = <V,T> × ds = φ(s)ds
avec T(dx/ds, dy/ds, dz/ds) et la seconde intégrale apparait comme la circulation d'un champ entre deux points, intégrale d'un gradient :
Notion de potentiel : »
|
Facteur intégrant d'une forme différentielle : |
Lorsque qu'une forme différentielle ω n'est pas exacte, c'est à dire lorsque ∂P/∂y ≠ ∂Q/∂x, on peut se poser la question de savoir s'il existe cependant une fonction f et une fonction k telles que ω1 = kω soit la différentielle de f. La fonction k est qualifiée de facteur intégrant.
En dimension 2 :
Il s'agit de rechercher (x,y) → k(x,y) afin que ω1 = k(x,y) × [P(x,y)dx + Q(x,y)dy] soit une différentielle exacte. La fonction k doit vérifier ∂(kP)/∂y = ∂(kQ)/∂x, ce qui consiste à résoudre l'équation aux dérivées partielles d'inconnue k :
∂k/∂y × P(x,y) + k × ∂P/∂y = ∂k/∂x × Q(x,y) + k × ∂Q/∂x
i/ Le problème est simple si l'on sait que k n'est fonction que d'une seule variable x ou y :
k × (∂P/∂y - ∂Q/∂x) - k' × Q(x,y) = 0
k × (∂Q/∂x - ∂P/∂y) - k' × P(x,y) = 0
Il s'agit d'équations linéaires homogènes du 1er ordre.
∗∗∗ On considère la forme différentielle ω = (x2 - y)dx + xdy. ∂P/∂y = -1 et ∂Q/∂x = 1. Il ne s'agit donc pas d'une forme différentielle exacte. Voyons s'il existe un facteur intégrant de la seule variable x : on aurait alors -2k - k'x = 0, d'où k(x) = α/x2 , α ∈R (» équ. diff. linéaire 1er degré). C'est tout bon ! Voyons s'il existe un facteur intégrant de la seule variable y : on aurait alors 2k - k'(x2 - y) = 0 : la solution dépend de x. Pas de facteur intégrant de ce type.
Si, dès lors, vous voulez intégrer la forme différentielle exacte ω1 = ω/x2, en appelant F une primitive, vous devez résoudre le système aux dérivées partielles ∂F/∂x = (x2 - y)/x2 = 1 - y/x2 , ∂F/∂y = 1/x . En intégrant ∂F/∂x, on obtient tout d'abord F(x,y) = x + y/x + φ(y). On dérive par rapport à y et on identifie : 1/x + φ'(y) = 1/x . D'où φ(y) = λ, λ ∈ R. Finalement :
F(x,y) = x + y/x + λ , λ ∈ R
ii/ Dans le cas général de cette dimension 2, avec ω = P(x,y)dx + Q(x,y)dy, l'équation différentielle du 1er degré P(x,y)dx + Q(x,y)dy = 0 admet une solution pouvant être exprimée sous la forme f(x,y) = λ ∈ R. En différentiant, on obtient :
 (df)
(df)
et, selon le théorème de Schwarz, les dérivées mixtes sont égales : ∂2f/∂x∂y = ∂2f/∂y∂x. Dire que les deux équations (df) et P(x,y)dx + Q(x,y)dy = 0 ont les mêmes solutions, c'est dire qu'elles sont colinéaires dans l'espace des formes homogènes du type Adx + By = 0, il existe donc un réel k, pouvant a priori dépendre de x et y, défini à un coefficient multiplicatif près, tel que kP = ∂f/∂x et kQ = ∂f/∂y. Et comme ∂(kP)/∂y = ∂2f/∂x∂y = ∂(kQ)/∂y, on définit ainsi une forme différentielle exacte :
ω1 = kω = k(x,y) × P(x,y)dx + k(x,y) × Q(x,y)dy)
∗∗∗ Reprenons le cas précédent de la forme différentielle non exacte ω = (x2 - y)dx + xdy. L'équation ω = 0 peut s'écrire xy' - y = -x2. L'équation linéaire homogène xy' - y = 0 a pour solution générale y = αx (» équ. diff. lin. du 1er degré). L'aspect polynomial du second membre -x2 et le facteur xy' conduisent à rechercher une solution particulière de l'équation complète de la forme βx2. On a alors 2βx2 - βx2 = -x2, donc β = -1 et la solution générale de l'équation ω = 0 peut s'écrire y = αx - x2 ou encore α = x + y/x = f(x,y). On doit avoir kQ = ∂f/∂y, soit kx = 1/x. Donc k(x,y) = 1/x2. Vérifions en ce qui concerne kP = ∂f/∂x : k(x2 - y) = 1 -y/x2 fournit bien le facteur intégrant k = 1/x2 qui s'avère fonction de x seul. On retrouver la solution trouvée précédemment.
Comme l'écrit Jean Bass dans son Cours de Mathématiques (» réf.1), on remarquera plus généralement encore que la solution f de (df) peut être remplacée par toute composée Φ o f où Φ désigne une fonction numérique dérivable d'une variable réelle telle que Φ o f = cte. En différentiant, on élargit le choix des facteurs intégrants qui sont alors donnés par :
kP = Φ'(f) × ∂f/∂x et kQ = Φ'(f) × ∂f/∂y
En dimension 3 :
Lorsque les conditions du théorème 2 ne sont pas vérifiées, on peut rechercher (x,y,z) →k(x,y,z) afin que :
ω1 = kω = k(x,y,z) × [P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz]
soit une différentielle exacte. Le problème est plus complexe car il conduit généralement à des difficultés d'intégration. En considérant le théorème 2 en dimension 3, on démontre le résultat suivant :
Une condition nécessaire et suffisante pour que ω
admette des facteurs intégrants est que le vecteur V(P,Q,R)
soit orthogonal à son
rotationnel, ce qui revient à écrire :

Lorsque la condition est vérifiée, on recherchera un facteur intégrant comme en dimension 2 : l'équation aux dérivées partielles P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz = 0 admet une solution que l'on écrira sous la forme f(x,y,z) = cte. Le facteur intégrant sera déterminé par kP = ∂f/∂x, kQ = ∂f/∂y et kR = ∂f/∂z
∗∗∗
a/ L'équation ω =
ydx + xdy - xydz est-elle exacte ?
b/ Montrer que l'équation ydx + xdy - xydz = 0 est intégrable et
l'intégrer. Justifier l'existence d'un facteur intégrant et le calculer
☼
Notions sur les équations aux dérivées partielles : »
➔ Pour en savoir plus :