
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
Espace L(E,F) | Anneau L(E) | Groupe GL(E) | Projecteurs | Symétries | Rotation | Similitudes | Groupe orthogonal O(E) et sous-groupes SL(E), SO(E) Matrices | Somme et produit de matrices | Matrice inverse | Trace d'une matrice | Valeurs propres | Matrices & changement de base |
Les applications linéaires constituent un chapitre considérable des mathématiques modernes, tant par sa densité au-delà de son développement propre comme le calcul matriciel, la théorie des déterminants, les formes quadratiques, les espaces fonctionnels, que par l'importance de son emploi dans les autres sciences (mais les mathématiques sont-elles une science ?) : recherche opérationnelle, sciences économiques, mécanique quantique, théorie de la relativité, du fait, en particulier, des nombreuses interventions des systèmes d'équations algébriques, différentielles ou aux dérivées partielles, dont la résolution utilise les applications linéaires et le calcul matriciel qui leur est lié. Les formes multilinéaires et les déterminants sont étudiés à part sur cette page.
∗∗∗
Des exercices sont proposés tout au long
de cette page et plus particulièrement ici
et là.
Dans toute la suite, on note +
l'addition d'un espace vectoriel E sur un corps commutatif K
(corps des scalaires,
généralement R ou C)
et au moyen d'un point (![]() •
•![]() ) sa multiplication par un scalaire.
Lorsqu'il n'y a pas d'ambiguïté, le point est souvent omis, Le
contexte fera comprendre de quelle loi
de composition il s'agit.
Le vecteur nul de E (neutre pour l'addition) est noté
0E. Dans un espace vectoriel de dimension finie n, une
base sera souvent notée (b1, b2, ...,
bn) ou (e1, e2,
...,en).
) sa multiplication par un scalaire.
Lorsqu'il n'y a pas d'ambiguïté, le point est souvent omis, Le
contexte fera comprendre de quelle loi
de composition il s'agit.
Le vecteur nul de E (neutre pour l'addition) est noté
0E. Dans un espace vectoriel de dimension finie n, une
base sera souvent notée (b1, b2, ...,
bn) ou (e1, e2,
...,en).
| Application linéaire, forme linéaire, endomorphisme, isomorphisme : |
On appelle ainsi un homomorphisme d'espaces vectoriels. C'est dire que si l'on appelle E et F deux espaces vectoriels sur le même corps commutatif K (pour simplifier l'écriture, leurs lois sont notées identiquement), et φ une telle application de E vers F :
On déduit de ces deux axiomes de définition :
Cette dernière propriété de nullité en zéro est une importante condition nécessaire de linéarité car elle peut servir pour prouver facilement qu'une application n'est pas linéaire dans la mesure où elle n'est pas vérifiée.
On peut réunir les deux axiomes de définition en un seul : pour tout couple (x,y) de E2 et tout couple (λ,μ) de K2 :
➔ Si deux espaces vectoriels sont isomorphes, on peut les identifier, en ce sens que parler des propriétés de l'un revient à parler de celles de l'autre car par l'isomorphie, tout résultat obtenu dans l'un peut être obtenu dans l'autre.
Endomorphisme, automorphisme :
Forme linéaire :
Lorsque F est le corps K des scalaires de E, une application linéaire de E vers K prend alors le nom de forme linéaire sur E. On peut parler aussi dans ce cas de fonctionnelle linéaire, mais cette appellation est désormais obsolète.
Exemples et contre-exemples :
1. R est un espace vectoriel de dimension 1 sur lui-même; les applications linéaires φ : R → R sont de la forme φ(x) = ax. Les applications de la forme φ(x) = ax + b avec b non nul ne sont pas linéaires; on parle d'application affine. Leur représentation graphique est cependant une droite, comme pour les applications linéaires de R dans lui-même. » Abonnement, exercice corrigé, fonctions affines niveau seconde.
2. Pour tout vecteur u d'un plan P, considéré comme un espace vectoriel de dimension 2 sur R, on pose φ(u) = 2u ; on définit ainsi un endomorphisme de P, appelée homothétie vectorielle de rapport 2.
3. Dans un plan vectoriel (espace vectoriel de dimension 2 sur R) rapporté à une base (i,j), considérer l'application f qui à tout vecteur v(x,y) associe v'(2x - y, x + y). On vérifiera facilement la linéarité de f.
4. Notons F l'espace vectoriel des fonctions numériques continues sur un intervalle [a,b] de R; l'application qui, à toute fonction f de F, associe l'intégrale <f , g> = ∫[a,b] f(t)dt est une forme linéaire sur F.
5. Soit f : R2 → R , f(x,y) = xy; f n'est pas linéaire : on n'a ni l'homogénéité, ni l'additivité. On donnera des contre-exemples numériques à foison...
6. Soit f : R2 → R , f(x,y) = x2/y si y non nul et 0 sinon. f n'est pas linéaire : l'homogénéité est vérifiée mais pas l'additivité.
7. Soit f : R2 → R , f(x,y) = xy; f est linéaire : f[(x,y) + (x',y')] = f(x + x', y + y') = (x + x') + (y + y') = (x + y) + (x' + y') = f(x,y) + f(x',y'). D'autre part f[λ(x,y)] = f(λx,λy) = λx + λy = λ(x + y) = λf(x,y).
8
. Soit g : R2 → R , g(x,y) = xy; g n'est pas linéaire : par exemple g(1,1) = 1 et g(2,2) = 4; or g(2,2) peut s'écrire g[(1,1) + (1,1)]; si g était linéaire, nous devrions obtenir g(2,2) = g(1,1) + g(1,1) = 2. Notons d'ailleurs que g[λ(x,y)] = g(λx,λy) = λ2xy donc distinct, en général, de λg(x,y)9
. Dans un espace vectoriel E, la translation de vecteur u non nul, définie par t(v) = v + u pour tout v de E n'est pas linéaire.
Applications affines (cas général) : » Noyau et image d'une application linéaire : »
∗∗∗
| Matrice d'une application linéaire : |
Lorsque E et F sont de dimensions
finies n et p, de bases
respectives B = (e1, ..., en) et B' =
(e'1, ..., e'p), la linéarité
d'une application φ : E → F permet d'écrire :
et cette relation caractérise une application linéaire : se donner l'application linéaire φ c'est se donner les vecteurs φ(e1), φ(e2), ... images par φ des vecteurs de la base B = (e1, ..., en) de E.
Considérons l'application
linéaire φ définie de R2,
base (i,j), dans R3, base (i,j,k),
par φ(i)
= 2i - 3j et φ(j)
= 3j + k.
Par linéarité : φ(v) =
φ(xi +
yj) =
xφ(i) + yφ(j) = x(2i
-3j) + y(3j + k) = 2xi
+ 3(y - x)j + yk : l'application linéaire
φ est bien
déterminée.
Dans le cas général, les coordonnées x', y', ... de φ(v) en fonction de celles de v sont des combinaisons linéaires de x, y, ... et ces formes caractérisent les applications linéaires. Exprimés dans la base B' = (e'1, ..., e'p) de F, les vecteurs φ(ei) sont de la forme :
- φ(e1) = a11
•
e'1 + a21
•
e'2 + ... + ap1
•
e'p
- φ(e2) = a12
•
e'1 + a22
•
e'2 + ...+ ap2
•
e'p
- φ(e3) = a13
•
e'1 + a23
•
e'2 + ... + ap3
•
e'p
- ...
- φ(en) = a1n
•
e'1 + a2n
•
e'2 + ... + apn
•
e'p
On appelle alors matrice de φ dans les bases B et B' le tableau des cordonnées, écrites en colonnes, de ces images :
 »
»
C'est une matrice à p lignes et n colonnes (matrice p x n).
Considérons l'exemple précédent : φ définie de R2 dans R3 par φ(i) = 2i - 3j et φ(j) = 3j + k. Dans la base (i,j,k), la matrice de φ s'écrit :

Si on note Mφ,B,B' cette matrice, on écrit souvent pour simplifier (en notant toujours en premier l'indice des lignes (i dans le cas présent) :
Lorsque n = p, on parle de matrice carrée d'ordre n. Lorsqu'il n'y a pas d'ambiguïté, on note simplement Mφ, voire tout simplement M, au lieu de Mφ,B,B'. Voici un exemple :
∗∗∗
Dans un espace vectoriel E de dimension 3 sur
R,
rapporté à la base B = (i, j,
k), on considère l'application linéaire φ
qui à tout vecteur v(x, y, z) associe
le vecteur v'(x - 2y + z, -x - y + 2z, -x + y). Donner la
matrice M de φ
dans la base B. ☼
Matrices d'applications linéaires associées aux transformations géométriques usuelles : »
♦ Somme de matrices :
Lorsque E et F sont de dimensions finies munis respectivement des bases B et B', considérons deux applications linéaires f et g de E vers F de matrices respectives Mf et Mg dans les bases B et B'.
La somme f + g de ces deux applications linéaires, définie par (f + g)(x) = f(x) + g(x) est manifestement linéaire. En notant :
f(ei) = a1i![]() •
•![]()
![]() e'1 + a2i
e'1 + a2i![]() •
•![]()
![]() e'2 +
a3i
e'2 +
a3i![]() •
•![]()
![]() e'3 + ... et g(
e'3 + ... et g(![]() e'i) = b1i
e'i) = b1i![]() •
•![]()
![]() e'1 + b2i
e'1 + b2i![]() •
•![]()
![]() e'2 + b3i
e'2 + b3i![]() •
•![]()
![]() e'3 + ...
e'3 + ...
la i-ème colonne de Mf + g est constituée des coordonnées de (f + g)(ei), c'est à dire a1i + b1i , a2i + b2i , ... , ani + bni. La matrice de l'application linéaire f + g est alors :
Mf + g = Mf + Mg = (aij + bij)i=1,..p ; j=1,..n » structures algébriques : cas (M2(R), +, ×)
Par exemple, dans le cas dimE = dimF = 2 :

!
Bien noter que l'addition de deux matrices n'a de sens que si elles sont de mêmes dimensions♦ Composée de deux applications linéaires et produit de matrices :
E, F et G sont des espaces vectoriels dimensions finies sur un même corps commutatif K et rapportés aux bases respectives B, B' et B". On considère les applications linéaires f : E → F et g : F → G et l'application composée h = g
o f : E → G. Vérifions que h est également linéaire : pour tout couple (x,y) de E2 et tout couple (λ,μ) de K2, on a, par linéarité de f puis de g :L'application composée de deux applications linéaires f : E → F et g : F → G est linéaire
On peut déterminer la matrice de h = g o f en calculant les images des vecteurs de base. Si Mh est cette matrice, elle sera, par définition, le produit Mg x Mf où Mf et Mg désignent les matrices de f et g dans les bases B et B' d'une part et B' et B" d'autre part.
! La composition des applications n'étant en général pas commutative, le produit Mg x Mf sera généralement distinct de Mf x Mg.
On constate alors que la matrice Mh s'obtient en faisant en quelque sorte, pour chaque terme hij cherché, le produit scalaire de la ligne i de Mf par la colonne j de Mg.
Par exemple, dans le cas dimE = dimF = dimG = 2 :

Dans le cas général, le
produit n'est possible que si le nombre de colonnes de la 1ère
matrice égale
le nombre de lignes de la seconde car l'espace d'arrivée de f est l'espace de départ de
g.
 → hij
= gi1f1j + gi2f2j + gi3f3j
→ hij
= gi1f1j + gi2f2j + gi3f3j
 Dans le cas
fréquent de
L(E), F = G = E,
avec dim E = n, on a :
Dans le cas
fréquent de
L(E), F = G = E,
avec dim E = n, on a :
! On voit par cette formule, que le produit de matrices dans L(E) n'est pas commutatif. Par exemple :

➔ Du fait de l'associativité de la loi de composition des applications, le produit de matrices est associatif.
♦ Matrice colonne (ou unicolonne) :
Dans un espace vectoriel de dimension n, il est souvent pratique d'écrire un vecteur v = x1e1 + x2e2 + ... + xnen sous la forme d'une matrice à n lignes et 1 colonne (vecteur colonne), ce qu'on écrit :

♦ Expression analytique d'une application linéaire :
Avec la notation matricielle précédente, l'image par une application linéaire φ de L(E,F) d'un vecteur v(x1, x2, ..., xn) de E (dimension n) sera le vecteur v'(x'1, x'2, ..., x'p) de F (dimension p) calculé par le produit matriciel :
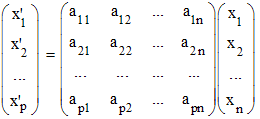
L'expression analytique de φ est l'expression des x'i en fonction des xi et aij :

➔ Remarquer que l'on a omis le signe optionnel de multiplication entre la matrice de l'application et le vecteur colonne v.
∗∗∗
E désignant un espace vectoriel sur R
de dimension 3, rapporté à une base B = (i,j,k),

Rép : 1/ Notons v'(x',y',z')
l'image de v(x,y,z) par φ; on a x' = x + y + z, y' = y + z, z' = -2x + z.
2/ La matrice de
φ o φ est A × A = A2
:

3/ Notons v"(x",y",z") l'image de v par φ o φ
: x" = x' + y' + z' = (x + y + z) + (y + z) + (-2x + z) = -x + 2y + 3z
y" = y' + z' = (y + z) + (-2x + z) = -2x + y + 2z , z" = -2x' + z' = -2(x + y +
z) + (-2x + z) = -4x - 2y - z.
Les coefficients de x", y" et z" correspondent bien aux lignes de la matrice
♦ Matrice unité :
L'application identique idE : v → v (ou simplement id) qui à tout vecteur v de E associe v lui-même, laisse inchangés les vecteurs de toute base; c'est dire que la matrice de l'application identique a tous ses termes diagonaux (ceux dont l'indice de ligne est égal à l'indice de colonne) égaux à 1, les autres sont nuls :

On note généralement In et on appelle matrice unité (ou parfois matrice identité), la matrice de l'application identique. La relation f o idE = idE o f = f se traduit par : Mf x In = In x Mf = Mf : In est l'élément neutre du produit de matrices carrées.
♦ Puissance d'une matrice carrée :
Dans le cas d'une matrice carrée n × n, on peut définir la puissance p-ème d'une matrice (p entier naturel) à la manière de celle d'un nombre :
Ao = I, matrice unité, ∀ p ≥ 2, Ap = Ap-1 × A
Ainsi A2 = A × A, A3 = A2 × A = (A × A) × A = (A × A) × A, ...
∗∗∗
1.

Calculer A2, A3;
En déduire une conjecture sur l'expression de An, n ∈ N. Vérifier par
récurrence.☼
2. E désignant un espace vectoriel sur R
de dimension 3,
on considère la matrice :

On pose B = A - I où I désigne la matrice unité d'ordre 3. Calculer B2 et B3; en déduire An, n ∈ N. ☼
♦ Matrice inverse :
Lorsque f est un endomorphisme bijectif (automorphisme) de matrice M relativement à une base B, la matrice de sa réciproque f-1 est appelée matrice inverse de M et noté M-1. On a alors :
M × M-1 = M-1 × M = In
Si l'on sait inverser la matrice M, on peut alors exprimer v en fonction de v' : c'est un moyen élégant de résolution d'un système d'équations linéaires n × n (n équations à n inconnues) car s'il admet une unique solution, ce type de système d'équations s'interprète comme l'expression analytique d'un automorphisme : v(x1,x2,...) désignant les inconnues, v'(x'1,x'2,...) désignant les constantes :

∗∗∗

Calculer A2 puis A2
- A. En déduire que A est inversible et exprimer A-1 en fonction de A
et I.
Rép. :
☼
et questions complémentaires (calcul de An)
(extrait de Problèmes de Mathématiques,
classe de Math. Sup., par jean Taillé, Éd. Vuibert 1966)
Calcul d'une matrice
inverse d'ordre 2 :
» Calcul d'une matrice inverse avec usage
des
déterminants :
»
Programme JavaScript du calcul d'une matrice inverse par
transfos élémentaires sur ses colonnes :
»
∗∗∗
| Espace L(E,F) et cas F = E : |
Si f est une application linéaire de E vers F et α un scalaire, notons αf l'application de E vers F qui, à tout v de E associe α.f(v). On définit ainsi une loi de composition externe dans l'ensemble, noté L(E,F), des applications linéaires de E vers F. Muni, de cette loi et de l'addition des applications, L(E,F) est un espace vectoriel sur K.
C'est dire, en particulier :
que la somme h = f + g de deux applications linéaires f et g de L(E,F) est linéaire; la matrice de h est obtenue en additionnant terme à terme les matrices de f et de g.
que l'application nulle, souvent notée θ, qui à tout v de E associe 0F est linéaire; la matrice de θ a tous ses termes nuls : matrice nulle.
que l'opposée de f dans L(E,F), notée -f et définie par (-f)(v) = -f(v) est linéaire; les termes de la matrice de -f sont les opposés de ceux de f; on dit que M-f est la matrice opposée de Mf.
que αf est linéaire pour tout α de K; la matrice de αf est obtenue en multipliant par k tous les éléments de Mf . On peut écrire :
M kf = k × Mf
que toute combinaison linéaire αf + βg + ... d'applications linéaires est linéaire.
En utilisant la notion de matrice ci-dessus, on montrerait facilement que :
♦ Si E et F sont de dimensions finies respectives n et p, alors L(E,F) est de dimension finie np. En particulier, si E = F, L(E,E) est noté simplement L(E), espace vectoriel des endomorphismes de E et dim L(E) = n2
.Si dim E = 1, les seuls endomorphismes de E sont ses homothéties : v → kv, k∈K. En effet, dans un tel espace, une base est constitué d'un quelconque vecteur non nul u et si f est un endomorphisme de E, on peut écrire :
Mais f(u) est un élément de E et il existe donc un élément k de K, tel que f(u) = ku. Par conséquent,
l'endomorphisme f apparaît ainsi comme l'homothétie de rapport k.
➔ Ce rapport dépend bien évidemment de f mais ne dépend pas de la base {u} choisie, sinon f ne serait pas une application : un élément pourrait alors posséder une infinité d'images; et si cet argument ne vous convainc pas, raisonnez par l'absurde, en changeant de base...
Anneau et algèbre L(E) :
Il est facile de montrer que si f est élément de L(E,F) et g élément de L(F,G), alors h = g o f est élément de L(E,G), la notation o désignant la loi de composition des applications.
En particulier si F = G = E, l'application composée de deux endomorphismes de E est un endomorphisme de E et on prouve facilement que muni de l'addition et de la loi de composition des applications, L(E) est un anneau unitaire, non commutatif dès que dim E > 1 et on peut aussi vérifier que muni de sa loi externe d'espace vectoriel définie précédemment, L(E) possède la structure d'algèbre.
∗∗∗
| Sous espaces vectoriels fondamentaux, image et noyau d'une application linéaire : |
Dans toute la suite l'acronyme sev signifiera sous-espace vectoriel. Quelques définitions et résultats fondamentaux que l'on pourra prouver facilement en utilisant ce théorème non moins fondamental :
Une partie non vide
P d'un espace
vectoriel en est un sous-espace vectoriel si et seulement si
toute combinaison linéaire d'éléments de P est un élément de P.
φ désignant une application linéaire, élément de L(E,F), l'étude de ces applications fait intervenir des sev fondamentaux comme :
♦ 1. L'ensemble Im(φ) des éléments de F images par φ des éléments de E. C'est un sev de F généralement noté Im(φ).
φ surjective ⇔ Im(φ) = F
♦ 2. L'ensemble des vecteurs u de E tels que φ(u) = 0
F est appelé noyau de φ. C'est un sev de E généralement noté Ker(φ). Cette notation provient de l'allemand Kern = noyau.φ injective ⇔ Ker(φ) = {0E}
Preuve : Supposons φ injective et v ≠ 0E un élément de Ker(φ); par injectivité, on a φ(v) ≠ φ(0E). Mais φ(0E) = 0F, donc φ(v) ≠ 0F : contradiction. Supposons maintenant Ker(φ) = {0E} : φ(v) = φ(w) ⇔ φ(v) - φ(w) = 0E ⇔ φ(v - w) = 0E ⇔ v - w ∈ Ker(φ). Mais Ker(φ) est réduit à 0E donc v = w et φ est injective.
➔ De 1 et 2, on conclut que :
L'application linéaire φ est bijective de E sur F ssi Ker(φ) = {0E} et Im(φ) = F
♦ Proposition :
Lorsque E et
F sont de même
dimension finie, en particulier lorsque E =
F et E de dimension finie,
la condition de bijectivité se réduit à Ker(φ) = {0E}
Preuve : cet important résultat devient évident en application du théorème des dimensions étudié in fine : dim Ker(φ) + dim Im(φ) = dim (E). Sir Ker(φ) = 0E alors φ est injective et dim Im(φ) = dim(E) = dim(F), donc Im(φ) = F : φ est surjective. En conclusion φ est bijective.
!
Si E et F n'ont pas la même dimension, le résultat ci-dessus est en défaut. Considérer l'applicationφ : R2 → R3 , φ(x,y) = (x,y,0)
φ est clairement linéaire, son noyau est réduit à (0,0), vecteur nul de R2, et φ n'est pas bijective puisque non surjective. De plus, la condition de dimension finie est indispensable : voir sur cette page (exercice 5), un exemple d'un endomorphisme d'un espace vectoriel de dimension infinie, non bijectif, de noyau nul.
♦ 3. l'ensemble des vecteurs de E invariants par φ, c'est à dire tels que φ(u) = u. C'est un sev de E, souvent noté Inv(φ).
♦ 4.
l'ensemble des vecteurs de E changés en leur opposé par
φ,
c'est à dire tels que φ(u) = -u.
C'est un sev de E, parfois noté Opp(φ).
♦ 4. Plus généralement, l'ensemble des vecteurs de E tels que φ(u) = λu, λ ∈ K est un sev de E. Lorsque u existe et est non nul, on dit que u est un vecteur propre de φ associé à la valeur propre λ.
En savoir plus sur les valeurs et vecteur propres d'un endomorphisme : »
| Projection vectorielle : ∗∗∗ |
On appelle projecteur ou projection vectorielle un endomorphisme π d'un espace vectoriel E vérifiant π o π = π. L'application identique idE vérifie cette propriété; c'est un automorphisme trivial. On suppose désormais que π est un projecteur distinct de idE.
a/ Montrer que π n'est pas bijectif : son noyau n'est pas réduit à {0E}.
b/ Montrer que l'image de E par π n'est autre que l'ensemble Inv(π) de ses vecteurs invariants. ☼
c/ Pour tout vecteur v de E, montrer que v + π(v) est invariant par π. En écrivant que v = π(v) + v - π(v), montrer que l'espace E est somme directe de Inv(π) et Ker(π) : E = Inv(π) ⊕ Ker(π).
Si vous séchez près avoir bien cherché :
☼Interprétation géométrique : appelons F l'image de E par π et G le noyau de π. On parle de projection vectorielle sur F, de direction G : tout vecteur v de E s'écrit vF + vG ∈F ⊕ G, donc π(v) = vF. La composante en F est invariante, la composante en G s'annule :

∗∗∗
1.
Dans L(E), on considère la
projection vectorielle p sur F, de direction G et on appelle conjuguée de
p la projection sur G, de direction F.
a)
Justifier l'équivalence : q est le conjugué de p ⇔
p + q =
idE.
b) Montrer que si p et q sont conjugués, alors p o q et q o p sont nuls.
Matrice d'une projection vectorielle π :
1. Toute matrice M vérifiant M × M) est une matrice de projection vectorielle.
2. Lorsque E et rapportée à une base B = (f1, .., fm, g1, ..., gp) réunion d'une base de F (= Im(π), vecteurs invariants par π) et d'une base de G (= Ker(π), vecteurs d'image nulle par π) avec m + p = dimE, la matrice de π est de la forme :


∗∗∗
Matrice d'une projection vectorielle
plane dans une base quelconque
Projection affine
|
Étude d'un anneau unitaire dans L(E)
| Symétrie vectorielle : ∗∗∗ |
On appelle symétrie vectorielle un endomorphisme s d'un espace vectoriel E vérifiant s o s = idE. On dit qu'une telle application est involutive. L'application identique idE vérifie cette propriété. justifier que -idE la vérifie également. On suppose désormais que s est une symétrie vectorielle distincte de idE.
a/ justifier que s est bijective (automorphisme de E)
i/ en utilisant la notion
d'élément symétrique)
ii/ en déterminant son noyau.
Concernant ii/ on suppose s(v) = 0 et on
applique s...
b/ Pour tout vecteur v de E, on note v' = s(v) son image par s. Montrer que v + v' est invariant par s et que v' - v est changé en son opposé.
c/ On pose F = {v, v∈E,
s(v) = v} et G = {v, v∈E,
s(v) = -v}. Montrer que E est somme directe
de F et G : E = F ⊕ G.
On parle de
symétrie vectorielle par rapport à F, de direction
G.
Interprétation géométrique :
Tout vecteur v de E s'écrit vF + vG
∈F ⊕
G,
donc s(v) = vF - vG.
La composante en F est invariante, la composante en G subit une symétrie
de direction G :
Matrice d'une symétrie vectorielle s :
1. Toute matrice M inversible et égale à son inverse (M = M-1) est une matrice de symétrie vectorielle.
2. Lorsque E et rapportée à une base B = (f1, .., fm, g1, ..., gp) réunion d'une base de F (vecteurs invariants s(v) = v) et d'une base de G (vecteurs changés en leur opposé s(v) = -v), avec m + p = dimE, la matrice est de la forme :

∗∗∗
∗∗∗
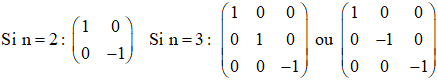
1.
Dans L(E), on considère la
symétrie vectorielle s par rapport à F de direction G et on appelle conjuguée de
s la symétrie par rapport à G de direction F.
Justifier l'équivalence : s' est la conjuguée de s ⇔ s' = -s
2. f et g sont deux symétries. Montrer que f o g est également une symétrie ssi
f et g commutent.
☼
la condition est clairement suffisante. Quant à la condition nécessaire,
supposer qu'il existe v tel que (f o g)(v) ≠ (g o f)(v).
Ces composées étant bijectives, on peut appliquer f puis g aux deux
membres de l'inégalité...
Symétrie vectorielle 2D |
Symétrie vectorielle 3D |
Étude d'un anneau unitaire dans L(E) |
Symétrie affine
| Le groupe linéaire GL(E) : |
Si h est linéaire et bijective de E sur F, alors sa réciproque h-1 est linéaire de F sur E; en effet, si au + bv est une combinaison linéaire d'éléments de F, h étant bijective, il existe un unique couple (x,y) d'éléments de E tels que h(x) = u et h(y) = v. Par suite :
h-1(au + bv) = h-1[ah(x) + bh(y)] = h-1[h(ax + by)](h-1 o h)(ax + by) = ax + by
Mais x = h-1(u) et y = h-1(v), donc :
Dans le cas E = F, on vérifie aisément que, muni de la loi de composition des applications, l'ensemble des bijections linéaires de L(E), appelées automorphismes de E, est un groupe. On l'appelle le groupe linéaire de E; on le note GL(E). Lorsque E est de dimension finie n, en identifiant une application linéaire à sa matrice dans la base canonique, on définit un isomorphisme de GL(E) sur le groupe Mn(K) des matrices carrées inversibles d'ordre n.
Groupe affine :
»| Le groupe orthogonal O(E), isométries vectorielles : |
Dans un espace vectoriel euclidien E (espace muni d'un produit scalaire), un endomorphisme conservant la norme est qualifié d'orthogonal. Ce sont des bijections de E (automorphismes). On parle aussi d'isométries vectorielles.
Proposition 1 :
L'automorphisme f conserve la norme si et seulement si f conserve le produit scalaire
Preuve : notons <u,v> le produit scalaire de deux vecteurs de E. Si f conserve le produit scalaire, on a pour tout u de E : <u,u> = <f(u),f(u)>, c'est à dire || u ||2 = || f(u) ||2, donc f conserve la norme. Si f conserve la norme, l'usage de la formule <u,v> = ½ (|| u + v ||2 - || u ||2 - || v ||2) et de l'égalité f(u + v) = f(u) + f(v) conduit à <u,v> = <f(u),f(v)>.
Proposition 1 :
Un automorphisme orthogonal transforme donc toute base orthonormée en une base orthonormée
! Conserver l'orthogonalité ne caractérise pas une isométrie. Considérer l'homothétie vectorielle f(v) = 2v.
∗∗∗
Les automorphismes orthogonaux de E constituent un groupe pour la loi de composition des applications appelé groupe orthogonal de E; on le note O(E). C'est un sous-groupe de GL(E), groupe linéaire de E.
➔ Plus généralement, lorsque E désigne un K-espace vectoriel muni d'une forme quadratique q, Les appellations groupe orthogonal et groupe spécial orthogonal sont aussi utilisées, un automorphisme orthogonal f signifiant alors q(u,v) = q(f(u),f(v)) pour tout u et v.
Le déterminant d'une isométrie est le déterminant de sa matrice. Il est égal à ±1 (»
preuve). On note O+(E) ou encore SO(E) le sous-groupe des automorphismes orthogonaux de déterminant +1, appelé groupe spécial orthogonal ou groupe spécial linéaire de E, noté alors SL(E).♦ Les rotations vectorielles :
En dimension 2 et 3, SO(E) correspond aux rotations vectorielles. Dans le plan, une rotation autre que l'identité n'admet aucun vecteur invariant à l'exception du vecteur nul. Dans l'espace, une rotation vectorielle admet une droite invariante (sous-espace de dimension 1) orthogonale à un plan globalement invariant ("plan de rotation"). La matrice d'une rotation
φ peut se ramener, dans une base orthonormée directe, à la forme :
L'angle θ de la rotation est déterminé par cos θ = a et sin θ = b. Si v = φ(u), alors l'angle orienté ^(u,v) mesure θ [2π].
Théorème :
Si on note <x,y> le produit scalaire de deux vecteurs de E, alors les assertions suivantes sont équivalentes :
f est une isométrie vectorielle de E.
f est une application de E vers E conservant le produit scalaire :
∀ (x,y) de E2 : <f(x),f(y)> = <x,y>
♦ Les symétries vectorielles orthogonales :
Les isométries de déterminant -1, parfois dites éléments de O-(E), ne constituent pas un groupe : la composée de deux telles isométries est un élément de O+(E). On parle parfois d'isométrie négative.
Une isométrie involutive, c'est à dire vérifiant f o f = id, coïncide avec sa réciproque et prend le nom, dans l'espace euclidien usuel, de symétrie vectorielle orthogonale (ou de réflexion vectorielle) lorsqu'elle est distincte de l'application identique. Il peut s'agir d'une symétrie vectorielle orthogonale par rapport à une droite ou par rapport à un plan.
Isométries affines : » ∗∗∗ Etude d'une symétrie vectorielle orthogonale
| Les similitudes vectorielles : |
Les composées v → k.f(v) d'une isométrie f et d'une homothétie de rapport k > 0 (v → kv), à savoir les similitudes vectorielles, constituent un sous-groupe de GL(E) généralement et malencontreusement noté GO(E).
![]()
Si k =
1, on retrouve le groupe orthogonal O(E) qui devrait être noté GO(E),
G pour groupe et O pour orthogonal...
Similitudes affines : »
| Théorème des dimensions : |
f désignant une application linéaire de E vers F, on suppose E de dimension finie n. On a alors :
dim Ker(f) + dim Im(f) = dim (E)
Preuve :
soit B = (b1, b2, ..., bn) une base de E.Si f est injective, le noyau de f est réduit au vecteur nul de E : on a Ker(f) = {0E}. Montrons que f(B) = {f(bi)}i = 1,2, ...,n constituent une base de Im(f) en considérant une combinaison linéaire nulle quelconque des f(bi) : Σαif(bi) = 0F. Par linéarité, on a f(Σαibi) = 0F. Le noyau de f étant réduit à 0E, on a Σαibi = 0E. Cette combinaison linéaire nulle des vecteurs de la base B a donc tous ses coefficients nuls. C'est dire que f(B) constitue une famille libre dans F. Étant génératrice dans Im(f), on en déduit qu'elle est une base de F et on a la relation 0 + n = n, autrement dit : dim Ker(f) + dim Im(f) = dim (E).
Si f est non injective, son noyau K est un sev de E de dimension au moins égal à 1. Soit k la dimension de K dont une base est du type B' = (b'1, b'2, ..., b'k). Selon le théorème de la base incomplète, nous pouvons compléter B' par n - k vecteurs v1, v2, ... vn-k afin d'obtenir une base de E. Ainsi tout vecteur v de E est une combinaison linéaire d'éléments de la base B'∪B", avec B" = (v1, v2, ... vn-k). Par suite, vu que f(b'i) = 0F, f(v) est combinaison linéaire des f(vj), j = 1, ..., n - k. B" est ainsi une famille libre et génératrice de Im(f) et on a k + (n - k) = n, autrement dit : dim Ker(f) + dim Im(f) = dim (E).
En application de ce théorème, reprenons l'exercice présenté ci-dessus (dimension 3) avec f : v(x, y, z) → v'(x - 2y + z, -x - y-x + y), on vérifiera facilement que Ker(f) est la droite vectorielle engendrée par u = i + j + k., donc de dimension 1. L'image de f est alors de dimension 2 (plan vectoriel) engendré par deux vecteurs indépendants extraits du système de vecteurs images {f(i), f(j), f(k)}. On peut choisir f(i) et f(j) car le déterminant,

extrait du tableau de coordonnées de ces vecteurs est non nul. » produit vectoriel
! Lorsque E = F, il arrive que Im(f) et Ker(f) soient supplémentaires dans E; cela se produit si et seulement si Ker(f)∩Im(f) = {0E}. On a trop tendance à penser qu'il en est toujours ainsi. Trois exemples simples et flagrants montrant que non, sont donnés dans l'exercice 4 de cette page.

Étude d'une symétrie vectorielle en dimension 3 :
L'espace E est de dimension 3 sur R; B = (i, j, k) est une base de E; on considère l'endomorphisme f de E dont la matrice relativement à B est :

i/ Calculer
M2 = M
x M. En
déduire que f est un automorphisme de E vérifiant
f-1 = f. (automorphisme
involutif ou
involution).
ii/ Montrer que
l'ensemble des vecteurs invariants par f est un sous-espace vectoriel
P de dimension 2 (plan vectoriel) engendré par u =
i + j et v = i - k.
iii/ Montrer que
l'ensemble des vecteurs changés en leur opposé est un sous-espace vectoriel D de dimension 1 (droite vectorielle)
engendré par w = i - j +
k.
4i/ En se rappelant
que la matrice de f dans la base (u,v,w) est
l'écriture en colonnes de f(u), f(v),
f(w) exprimés dans cette base, montrer que la matrice de f dans la base (u,
v, w) est :

On dit que f est la symétrie vectorielle par rapport à P suivant la direction D.