ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 JORDAN
Camille Marie-Ennemond, français,
1838-1922 |
Reçu 1er au concours d'entrée à l'École polytechnique, Jordan fut tout d'abord ingénieur de Mines en province puis à Paris (1867) où il débute une nouvelle carrière : professeur à l'École polytechnique (1876), il enseigne aussi au collège de France (dès 1875) et succède à Liouville (1883) en assurant le suivi de son Journal de mathématiques pures et appliquées.
Jordan succédera également à Chasles à l'Académie des sciences en 1881. Ses travaux portent essentiellement sur l'algèbre linéaire et les structures algébriques (théorie des groupes en particulier) ainsi que sur les premiers développements, avec Borel, de la théorie de la mesure des ensembles dont s'emparera magnifiquement Henri Lebesgue avec la mise en place d'une définition rigoureuse de l'intégrale d'une fonction numérique.
Dans son Traité des substitutions et des équations algébriques (1870), il rend hommage aux travaux de Galois et complète sa théorie des groupes (sous-groupe distingué, groupe résoluble, groupe quotient, étude des groupes infinis) et achève la résolution des équations algébriques de degré quelconque (les résultats de Galois concernaient un degré premier). C'est à Weber (1893) que l'on devra la définition axiomatique d'un groupe abstrait non nécessairement fini. L'étude du groupe linéaire des applications linéaires de Cn dans lui-même lui permet de découvrir des méthodes de réduction des matrices.
Par la précision du langage et la rigueur de ses exposés, les cours d'analyse de Jordan, donnés à l'École polytechnique (1882-1887), restent encore aujourd'hui une référence (» réf.2). Ce grand mathématicien est le petit-fils du politicien français Camille Jordan (1771-1821).
| Courbes de Jordan, arcs & surfaces de Jordan : |
Le concept de courbe n'est pas simple. Jusqu'à cette époque une courbe était algébrique : définie par une expression polynomiale ou bien unicursale (paramétrée). Une courbe peut être considérée comme le bord d'une surface. Dans ce contexte, le développement de la topologie avec la notion d'intérieur et d'extérieur nécessitait une redéfinition, voire une classification.
Rappelons à ce propos que depuis Möbius et son fameux ruban, on sait qu'une surface peut n'avoir ni intérieur ni extérieur ! L'apparition des courbes fractales quelques décennies plus tard avec Peano, Koch, Julia et Mandelbrot révolutionnera cette branche de l'analyse et nécessitera des définitions et des outils d'étude encore plus complexes.
On peut ainsi définir une courbe de Jordan :
image du cercle unité de R2 (de centre O de rayon 1) par une fonction continue et injective à valeurs dans Rn ( n ≥ 2)
Les ensembles R2 et Rn sont ici assimilés à des espaces métriques affines. En tant qu'image continue d'un cercle, une courbe de Jordan est fermée. L'injectivité exprime qu'une telle courbe n'admet pas de points doubles : c'est une courbe simple. En d'autres termes :
On appelle courbe de Jordan une courbe simple et fermée de l'espace R
n
Ci-dessus, le "nœud de trèfle", courbe fermée de l'espace R3, sans point double (» théorie des nœuds). C'est un exemple de courbe de Jordan, également appelée courbe de Hoppe dont une équation peut s'écrire x = cost(3cost + 2), y = 5sintcost, z = sint(25cos2t - 1) : source Alain Bouvier. On trouvera également sur le site de Robert Férreol, le nœud de trèfle et ses équations.
i
Reinhold Hoppe, mathématicien allemand (1816-1900). Travaux en analyse et géométrie différentielle, courbes & surfaces.Dans le cas d'une courbe plane, on peut définir une courbe de Jordan sans faire allusion au cercle de la manière suivante :
courbe définie par une fonction continue périodique f : t → (x(t),y(t)) dont la restriction à tout intervalle [t, t + T[ est injective
➔
Concrètement, il s'agit de courbes fermées simples dont on peut définir un intérieur et un extérieur. Un contre-exemple : la lemniscate de Bernoulli.Dans le plan, toute courbe de Jordan est homéomorphe au cercle unité : deux courbes de Jordan s’échangent par homéomorphisme (bijection continue dont la réciproque l'est aussi : bijection bicontinue).
Topologiquement, une courbe de Jordan est compacte et connexe. C'est aussi un lacet (mais un lacet n'est pas toujours une courbe de Jordan).
On a ce résultat fondamental :
Dans le plan, le complémentaire d'une
courbe de Jordan (C) possède deux composantes connexes de frontière (C).
L'une est bornée : intérieur de (C), la seconde ne l'est pas : extérieur
de (C).
Ensembles et espaces connexes, notion d'homotopie : »
Arc de Jordan :
On appelle ainsi l'image d'un intervalle fermé J = [a,b] de R par une application continue et injective de J dans Rn. Un tel arc est donc homéomorphe à un segment. On doit à Jordan le concept d'arc rectifiable, c'est à dire dont on peut calculer la "longueur".
Rectification d'un arc de courbe : »
Surface de Jordan :
Ces surfaces sont à l'espace ce que les courbes sont au plan : elles sont l'image de la sphère unité de R3 par une fonction continue et injective à valeurs dans Rn (n ≥ 3). La sphère, l'ellipsoïde sont des surfaces de Jordan. Le ruban de Möbius n’en est pas une (on ne peut y définir un intérieur et un extérieur). Ces notions se rattachent à la topologie différentielle.
| Mesure de Jordan : |
à la frontière de la topologie et de
l'analyse numérique, l'étude des surfaces conduit Jordan à s'intéresser à ce
que l'on appelle aujourd'hui la théorie de la mesure
(ensembles et fonctions mesurables) que développera Borel.
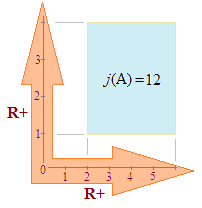
La mesure de Jordan pour une partie bornée A de R
2 est une mesure de son aire, consistant à l'approcher extérieurement et intérieurement par des rectangles, mesurés en unités d'aires indépendamment de toute unité dans un repère orthogonal quelconque. Dans Rn, on parlerait de pavés et de volumes.Si la mesure extérieure j+(A) coïncide avec sa mesure intérieure j-(A) sans dépendre des rectangles utilisés, la partie A est dite mesurable au sens de Jordan et on dit que A est j-mesurable en notant j(A) cette commune mesure. Cette définition n'est pas sans rappeler les sommes de Riemann (ou de Cauchy) d'une fonction positive (encadrement de l'aire sous la courbe par des rectangles).
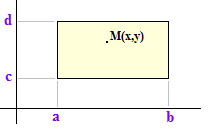
Contre-exemple : Considérons dans R2, l'ensemble A des points M(x,y) à coordonnées rationnelles inclus dans le rectangle K = [a,b] x [c,d]. La mesure extérieure de A est celle de K : j+(A) = (b - a)(d - c). Vu que les rationnels de A sont dénombrables, on peut les numéroter q1, q2, ... et considérer que A est la réunion de pavés Rn, rectangles réduits aux singletons {qn}. On a j(Rn) = 0 pour tout n. Cette approche intérieure conduit donc à j-(A) = 0 distinct de j+(A). A n'est donc pas j-mesurable.
➔
Ce contre-exemple est à rapprocher de l'intégrale de la fonction caractéristique de Q sur un intervalle [a,b] : nulle au sens de Lebesgue, non définie au sens de Riemann.On a les résultats suivants :
Si f est une fonction positive sur [a,b], l'aire du domaine A situé sous la courbe est j-mesurable si et seulement si f est intégrable au sens de Riemann et dans ce cas :
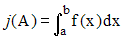
Une partie bornée de Rn est j-mesurable si et seulement si sa frontière l'est aussi et de j-mesure nulle.
Les notions de mesure d'ensemble et d'intégrale sont
étroitement liées. La mesure de Jordan, basée sur la notion élémentaire d'aire,
s'avéra insuffisante pour mesurer des ensembles "pathologiques", comme les
ensembles fractals. Plus gênant : une
réunion dénombrable d'ensembles j-mesurables
peut ne pas être j-mesurable.
Ce constat conduisit aux travaux de Borel et à
l'intégration au sens de Lebesgue.
| Homomorphisme (ou simplement morphisme) de structure, automorphisme, isomorphisme : |
On doit à Jordan le concept d'homomorphisme (du grec homoios = semblable et morphê = forme) entre deux structures algébriques :
Si (G,∗) et (H, •) sont deux magmas (ensembles munis d'une loi de composition interne), on dit qu'une application φ de G dans H est un homomorphisme de (G,∗) dans (H, •) pour exprimer que :
∀ (a,b)∈G
x G :
φ (a∗b) = φ (a)
•φ (b)
On dit que φ respecte les lois de G et H ou bien que φ est compatible avec ces lois.
Soit n un entier naturel non nul distinct de 1. Pour tous rationnels x et y, on a nx + y = nx × ny (fonction puissance). L'application φ : x → nx est un morphisme de (Q,+) dans (R+,×).
➔ Dans le cas d'ensembles munis de plusieurs lois de composition, un homomorphisme doit respecter chacune des lois. Au lieu d'homomorphisme, on parle souvent simplement de morphisme.
Un homomorphisme bijectif est appelé isomorphisme, du grec isos = égal et morphê = forme. Lorsque H = G, un homomorphisme est appelé endomorphisme et s'il est bijectif, on parlera d'automorphisme.
La fonction logarithme est un isomorphisme du groupe multiplicatif (R+-{0}, x) sur le groupe additif (R,+) car Log(a × b) = Log a + Log b.
En savoir plus sur les homomorphismes de structures algébriques : »
| Matrices de Jordan : |
Ces matrices se rencontrent dans la triangulation des matrices carrées (certains parlent de trigonalisation) : mise sous forme triangulaire. Les éléments placés au-dessous de la diagonale (ou bien au-dessus, selon la base choisie) sont nuls.
Dans M4(R), espace vectoriel des matrices carrées 4 × 4, une matrice de Jordan est de la forme :
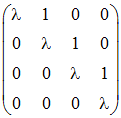
Dans Mn(R), espace vectoriel des matrices carrées n × n, on appelle bloc de Jordan d'ordre m ≤ n de valeur propre λ, une matrice carrée m × m de la forme ci-dessus.
Lorsque K = C, toute matrice carrée peut se mettre, au moyen d'un changement de base approprié, sous la forme :
où les blocs Δi sont des blocs de Jordan. Dans Mn(R), une matrice peut être mise sous cette forme si celle-ci admet n valeurs propres éventuellement multiples.
Matrices et algèbre linéaire : »
Théorème de Jordan : » Il concerne l'intégrale d'une fonction d'une variable complexe sur un arc de cercle : Si f est continue sur un cercle de centre
zo, de rayon R et si la limite de |(z -
zo)×
f(z)| est nulle lorsque
Lemme de Jordan :
R tend vers l'infini, alors
l'intégrale sur tout arc de ce cercle est nulle.
| Fonction (numérique) à variation bornée : |
C'est Jordan qui définit pour la première fois cette notion lors de ses travaux sur la rectification des courbes :
Soit f une fonction numérique définie en tout point d'un segment [a,b] et S = (xi) i=1,...n une subdivision quelconque de cet intervalle (non nécessairement régulière) : a < x1 < x2 < x3 < ... < xn = b. Considérons le nombre :
S'il existe un réel M indépendant de S tel que V(f,xi) < M, on dit que f est à variation bornée sur [a,b] et la borne supérieure de l'ensemble des V(f,xi) est la variation ou l'oscillation de V[a,b] de f sur [a,b].
Toute fonction f à variation bornée sur un intervalle J, s'écrit f = g - h où g et h sont à variation bornée sur J.
Toute fonction monotone sur un intervalle [a,b] est à
variation bornée
Si f est intégrable au sens de Riemann sur [a,b] alors la primitive :
est à variation bornée et :
Grâce à ce nouveau concept, Jordan généralise un résultat de Dirichlet concernant la convergence des séries de Fourier :
Si f est une fonction 2π-périodique à variation bornée, alors la série de Fourier de f converge vers ½[f(x+) + f(x-)]
➔ Pour en savoir plus :
Gibbs