
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Transformée de Fourier , produit de convolution au sens de Laplace , au sens de Fourier |
La transformation de Laplace intervient dans la résolution d'équations et de systèmes différentiels et tout particulièrement aujourd'hui en électricité, électronique, théorie de la chaleur, théorie du signal, ... :
Si f est une fonction numérique nulle en dehors de R+, sa transformée de Laplace est la fonction qui à tout nombre réel ou complexe p associe :
Cette transformée peut ne pas exister (divergence de l'intégrale) au voisinage de l'infini. Noter que si p est imaginaire pur, on retrouve la transformée de Fourier d'une fonction f nulle en dehors de R+. Les cas usuels, notamment appliqués au calcul d'intégrales ou à la résolution d'équations différentielles d'ordre n, qui se ramènent à des équations polynomiales de la forme Lf (p) = Pn(p), font intervenir le cas p réel, cas sous-entendus ci-après.
➔ La résolution d'une équation différentielle F(y,y',y",...) = 0 consistera alors à savoir inverser la transformée de Laplace de y (retrouver f connaissant Lf), ce qui s'avère souvent plus simple que la résolution de l'équation différentielle initiale (usage de tables). On parle de calcul symbolique car des objets mathématiques de nature différente sont ici substitués : calcul fonctionnel ↔ calcul algébrique. » exemple 5 ci-après
| Deux résultats concernant les limites : |
![]()
|
Conditions suffisantes d'existence : |
Une condition moins forte est la continuité de f par morceaux sur tout intervalle borné de [0 ,+∞[ et vérifie sur [0 ,+∞[, une majoration de la forme :
où M > 0 est indépendant de t et a est un réel à déterminer. Alors la transformée de Laplace existera pour tout p > a.
| Quelques exemples usuels de transformées (les écritures p > 0 ou p > a sous-entendent p réel, t est positif) : |
|
|
|
|
|
|
|
|
|
Ha = H(t - a) |
p → e-ap/p |
p > 0 |
|
|
|
|
|
|
|
p > 0 |
|
|
(preuve : dans l'intégrale, poser u =pt) |
|
|
f(t) = 1/√t (α = ½) |
Γ(½)/p½ = √π/√p » fonction Γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| f(t) = ln t | p → - (ln p + C)/p » constante d'Euler | |
|
|
p → Lf(p)/p » exercice | |
|
|
|
|
|
f(t) = eat × sin bt |
p → b/[(p - a)2 + b2] |
p > a |
|
f(t) = eat × cos bt |
p → (p - a)/[(p - a)2 + b2] |
p > a |
|
|
|
|
| Linéarité : |
La transformation de Laplace est linéaire, c'est à dire :
| Théorème du retard (translation) : |
Pour t ≥ a, considérons Φ : t → f(t - a); alors :
| Transformée d'un produit de convolution : |
Lorsque le produit x → f(t - x)g(x) est intégrable sur tout intervalle [0,t] de R+, le produit de convolution de f et g, au sens de la transformation de Laplace, est la fonction f * g définie par :
![]()
et l'on montre que :
Lf *g = Lf × Lg
➔ L'intégrale de convolution peut porter sur [0,+∞[ , mais les fonctions f et g étant nulles en dehors de R+, l'intégrale sur [t,+∞[ est nulle, ce qui ramène à [0,t].
Cas de la transformée de Fourier : »
| Transformées de la dérivée et de la primitive : |
Une simple intégration par parties montre facilement que :
Par suite, si F désigne la primitive de f nulle en 0, (intégrale sur [0,t] de f) , on a F'(t) = f(t), d'où :
LF(p) = Lf(p)/p
On peut ensuite obtenir :
et, par récurrence, les transformées de Laplace des dérivées troisième, quatrième, etc.
| Inversion de la transformée de Laplace : |
En l'absence de tables, comme ci-dessus, et dans un contexte plus subtil, la recherche de f(t) connaissant sa transformée F(p) peut être très difficile. Il s'agit de résoudre, sous certaines (bonnes) conditions de de "régularité" (continuité, dérivabilité sauf peut-être en un certain nombre fini de points) l'équation intégrale (l'inconnue fonctionnelle f est sous le signe d'intégration) :
![]()
L'existence de f est liée l'holomorphie de F (dérivabilité de F pour p complexe) et utilise l'inversion de la transformation de Fourier (formule de réciprocité).
Heaviside et les règles d'inversion : »
∗∗∗
1. Prouver que la transformée de Laplace de t → tn est p → n!/pn+1. Préciser la convergence ☼
2. Prouver que la transformée
de Laplace de t →
eat
est p
→ 1/(p
- a). Préciser la convergence.
☼
(on supposer ici a et p complexes)
3. Prouver que la transformée
de Laplace de t →![]() est p
→ Lf(p)/p
☼
est p
→ Lf(p)/p
☼
4. Prouver que la transformée de Laplace de t → f(at) (a > 0) est p → Lf(p/a)/a ☼
5. On considère l'équation différentielle linéaire du second ordre d'inconnue y = f(t) :
y" - y' = sin 2t , avec : y(0) = y'(0) = 1.
On note Y = Lf(p) la transformée de Laplace de y = f(t).
a/

b/ Montrer que l'on peut écrire Y sous la forme (décomposition d'une fraction en éléments simples) :
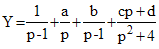
et que a = -1/2 , b = 2/5 , c = 1/10, d = -2/5.
c/ En utilisant le tableau ci-dessus, montrer par inversion que :
➔ Pour en savoir plus :
Des MathÉmatiques pour les Sciences,
par Caude Aslangul (univ. Paris 6). Concepts, méthodes et techniques pour
la
modélisation.
Éd. De Boeck - Bruxelles, 2011.
Transformée de Laplace, pages de Claude Saint-Blanquet et Bernard
Fourcher (univ. de Nantes) :
http://www.sciences.univ-nantes.fr/physique/perso/blanquet/conducti/61laplac/61laplac.htm
Transformation de Laplace
par Elie Raphael,
professeur à l'ESPCI :
http://www.espci.fr/enseignement/maths/PourAllerPlusLoin/C_Barreteau/documents/polymaths1A_051212_Chap4.pdf
Tables de transformées de Laplace : http://eqworld.ipmnet.ru/en/auxiliary/aux-inttrans.htm