ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Coordonnées en dimension 3 : sphériques, paramétriques, cylindriques,      géographiques, géocentriques (géodésiques), horizontales (azimutales), équatoriales       » Sphère céleste | Latitude et longitude | Coordonnées curvilignes | coordonnées paramétriques & polaires (cas du plan)

Tout point de l'espace 3D est déterminé sans ambiguïté dans un repère orthonormé (0,x,y,z), dit cartésien :

• x est l'abscisse de M;

• y est son ordonnée;

• z est sa cote    (prononcer le o de cote comme dans mon pote, et non pas côte comme dans j'ai eu du pot...)

Dans de nombreux cas, un paramétrage trigonométrique, analogue aux coordonnées polaires (r, θ) du plan, s'avère fructueux :

On se convaincra facilement que la donnée  :

• du module OM = r (positif a priori mais on peut dans certains cas le considérer réel quelconque par commodité);

• de l'azimut : ^(Ox,OH) = θ;

• de la hauteur : ^(OH,OM) = φ, qui sont des angles orientés, caractérise un point de l'espace.

Le triplet (x,y,z) constitue les coordonnées du vecteur OM. Pour cette raison, lorsque r désigne la distance OM, donc la norme de OM, r est appelé rayon-vecteur. L'application de la trigonométrie élémentaire dans la figure ci-dessus conduit aisément, pour tout point M(x,y,z) de l'espace à :

x = r.cosφ.cosθ , y = r.cosφ.sinθ , z = r.sinφ     (cp) 

Sous la forme (cp), on parle de coordonnées paramétriques d'un point de l'espace.

♦ Coordonnées sphériques :    

La donnée de r, θ, et φ vérifiant la relation (cp) revient à se donner le point M de la sphère de centre O de rayon r :  on vérifie aisément que x² + y² + z² = r². K désignant la projection orthogonale de M sur le plan de l'équateur, le triplet (r, θ, φ) constitue les coordonnées sphériques de M. Dans ce repère, le plan (xOy) d'équation z = 0 est l'équateur de la sphère.

 ➔  Noter que les coordonnées paramétriques (r,θ) d'un point du plan, x = r.cosθ et y = r.sinθ pourraient être dites circulaires puisque x² + y² = r².

♦ Coordonnées cylindriques :    

Le triplet (r, θ, z) où (r,θ) désigne le couple de coordonnées polaires de M dans le plan (xOy), constitue les coordonnées cylindriques de M (» justification de cette appellation).

♦ Coordonnées géographiques, latitude, longitude :     

En géographie, un point du globe terrestre est défini par sa latitude, angle φ = ^KOM et sa longitude, l'azimut θ = ^xOK.

Pour cette dernière, le méridien contenant (xOz) est le méridien origine : De nos jours, il s'agit du méridien passant par les pôles nord et sud et l'observatoire de Greenwich (commune de Londres située sur la Tamise, au sud de la ville), donc, par définition, de longitude 0°. Le système mondial de positionnement GPS (» réf.6) mis au point par le gouvernement des États-Unis (Global Positioning System) permet de localiser de façon précise tout lieu de la planète au moyen de 24 satellites géostationnaires. L'avènement des smartphones a permis à tout un chacun de posséder un système de navigation routière extrêmement efficace. Il est aussi utilisé dans les transports maritimes et aériens.

                 Parallèles et méridiens : »            

• La latitude varie de 90°sud (90° S) à 90°nord (90° N). L'hémisphère contenant [Oz) est l'hémisphère nord. On peut aussi mesurer les latitudes de 0° à +90° dans l'hémisphère nord et de 0° à -90° dans l'hémisphère sud. Tous les points (lieux) situés sur un même parallèle ont même latitude.

• Le rayon d'un parallèle s'obtient par r_p = R × cosφ, R désignant le rayon équatorial de la Terre.

• La longitude varie de 180° Ouest à 180° Est. On peut également mesurer les longitudes positivement vers l'est et négativement vers l'ouest.

• Exemples (à 1 minute près) :
  - Paris (cathédrale Notre-Dame) a pour latitude 48° 52' N et pour longitude 2° 19' E.
  - New York : 40° 42' , -74° (74° Est)

Méchain, le bureau des longitudes et les fuseaux horaires : »

♦ Coordonnées géocentriques ou géodésiques :      

Il s'agit d'un repère cartésien local, orthonormé direct (O,x,y,z) dont la Terre est l'origine, le méridien contenant Ox étant celui de l'observateur. Il voit son usage en cartographie.

Loxodromie et orthodromie : »          »  Mercator Gerhard Kremer , Nonius , Girard , Delambre , Biot

♦ Coordonnées horizontales (azimutales), hauteur, vertical, distance zénitale :    

Il s'agit, en astronomie, d'un système de coordonnées locales. On considère un observateur O à la surface de la Terre.

• (Oz) désigne la direction du zénith de l'observateur (au-dessus de sa tête) : verticale ascendante, autrement dit (Tz) où T désignerait le centre de la Terre; On peut aussi parler de la direction d'un fil à plomb bien connu des maçons : verticale descendante (On) passant par T, le nadir.

• L'une ou l'autre de ces verticales permet de définir l'horizon de l'observateur : plan (H) passant par O, perpendiculaire au zénith (Oz), soit, localement, le disque "horizontal" passant par O.

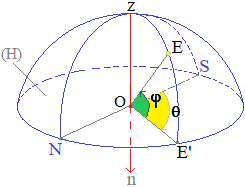
• L'observateur note sur l'horizon la direction d'un des points cardinaux (Nord, Sud, Est, Ouest) ou tout autre point de son choix  qui servira d'origine pour la mesure de l'azimut local θ = ^SOE' (ci-dessus avec S comme origine), compté de 0° à 360° dans le sens des aiguilles d'une montre (sens horaire, également dit rétrograde).

• Si E désigne une étoile observée, le plan vertical contenant (Oz) et E, appelé le vertical de E, coupe l'horizon en E'.

• L'angle h = ^E'OE est la hauteur (locale) de E.

• Le couple (θ,h) constitue les coordonnées horizontales ou coordonnées azimutales de l'étoile E pour l'observateur O. L'angle ^EOZ = 90° - h, complémentaire de h, est la distance zénithale de E.

Latitude et hauteur du pôle : »           » Pythéas de Massalia

♦ Sphère céleste, pôles célestes et équateur céleste  :    

En astronomie, on parle de sphère céleste pour désigner une sphère imaginaire (totalement translucide) de rayon arbitraire (indéterminé ou infini, peu importe) sur laquelle serait placées les étoiles (localement, on parle communément de voute céleste ou de voute étoilée). lus précisément, l'observateur terrestre d'un astre A voit sa projection p_A sur la sphère céleste, alignée avec le centre T de la Terre.

• L'axe du monde n'est autre que l'axe de rotation de la Terre, défini par les pôles nord et sud de cette dernière (de latitudes respectives 90° N et 90° S). Vue au-dessus du pôle nord, la Terre tourne dans le sens inverse des aiguilles d'une montre (autrement dit le sens trigonométrique).

• Comme la sphère céleste, les pôles célestes sont également imaginaires. Situés sur l'axe du Monde, ils percent la sphère céleste (figure ci-dessous) en P_n et P_s.

• Le plan de l'équateur terrestre (en bleu) est l'équateur céleste; c'est un plan de la sphère céleste (limité à un disque de centre T dans les représentations).

Point vernal, précession des équinoxes :    

On sait que l'axe de rotation de la Terre est incliné par rapport à son plan de révolution autour du Soleil, l'écliptique (en jaune ci-dessous), selon un angle d'environ 23° 27'. L'équateur céleste rencontre l'écliptique selon la droite des équinoxes (γΩ) ci-dessous (Ω est souvent nommé γ'). Le point γ est appelé point vernal (issu du latin ver, veris = printemps, qui a aussi donné primavera = printemps en italien et primevère, autrement dit première fleur de printemps).

➔  Le point vernal γ n'est pas fixe, il se déplace chaque année sur l'équateur d'environ 50 secondes d'arc dans le sens rétrograde (sens "horaire") tant et si bien qu'il fait le tour de l'écliptique en 26 000 ans : on parle de précession des équinoxes (précession puisqu'elles se produisent 50" plus tôt chaque année), constatée pour la première fois par le brillant astronome grec Hipparque de Nicée vers 150 av. J.-C.

Coordonnées équatoriales d'un astre, ascension droite, déclinaison, année tropique :   

• Ci-dessus, le plan horizontal est l'équateur céleste, T est le centre de la Terre. Le point vernal γ est choisi comme origine des azimuts. Dans ce repère céleste, l'ascension droite de A est l'azimut α de p_A et sa déclinaison est la hauteur δ de p_A. Le couple (α,δ) définit les coordonnées équatoriales de l'astre A.

 i  L'ascension droite α du Soleil augmente en moyenne d'environ 1° par jour car en un an, soit environ 365,25 jours, tout se passe comme si ce dernier "parcourait" l'écliptique en décrivant 360° et 360/365.25/ ≈ 0,9856°. L'intervalle de temps séparant le passage du Soleil au point γ est l'année tropique : ascension nulle, le Soleil traverse le plan de l'équateur, médiateur des tropiques du Cancer (hémisphère nord, parallèle de latitude +23°27') et du Capricorne (hémisphère sud, parallèle de latitude -23°27') :

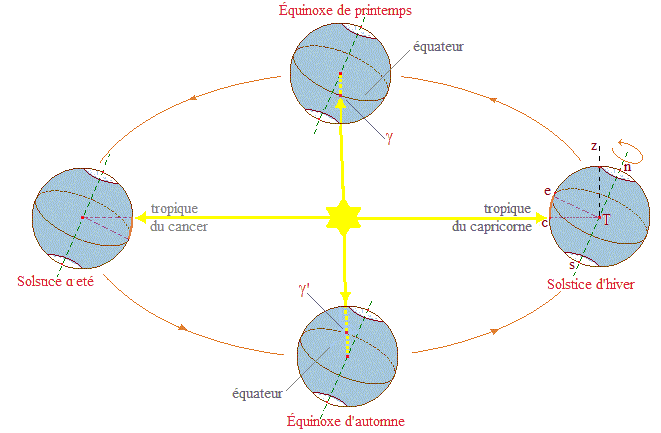
Du fait de l'obliquité de l'écliptique évoquée ci-dessus, la déclinaison du Soleil est (graphiquement) sinusoïdale variant périodiquement sur une année de -23°27' (solstice d'hiver) à + 23°27' (solstice d'été). Ces considérations ont permis aux astronomes de définir une mesure précise du temps (au sens temporel, pas de la météo...).

Méchain et la mesure du temps : »

 i  Si la Terre n'était pas inclinée par rapport au plan de l'écliptique, il n'y aurait pas de saisons, son ensoleillement serait quasiment constant (petites variations eu égard à son orbite elliptique). Le Soleil se lèverait constamment plein Est et se coucherait plein Ouest.

En savoir un peu plus sur le lever/coucher du Soleil : »       » Hipparque , At-Tusi             

La célèbre Étoile polaire :

En astronomie, les étoiles d'une constellation sont généralement dénommées au moyen des lettres de l'alphabet grec α, β, γ, δ, ε, ... Dans l'hémisphère nord, l'axe du monde (P_sP_n) pointe actuellement vers l'étoile α de la constellation de la Petite Ourse (sans rapport avec la terminologie α de l'ascension droite), dite étoile polaire, de déclinaison δ = 89° 15' N, d'ascension droite α = 2h 31'. Compte tenu, en particulier, de la précession des équinoxes, l'axe de rotation de la Terre subit de légères variations de sa direction (» réf.3-4).

 i  Dans l'hémisphère, afin de s'orienter de nuit vers le Sud, on utilise une constellation mythique : la Croix du Sud que l'on rencontre sur le drapeau de nombreux pays de l'hémisphère austral et matérialisée sous forme de pendentif comme ci-dessous à droite. Croix du Sud fut le nom donné à son hydravion par Jean Mermoz, illustre aviateur français, dans lequel il disparait avec son équipage dans l'océan Atlantique, au large de Dakar, le 7 décembre 1936.

♦ Relation entre latitude, hauteur et déclinaison d'une étoile :    

Considérons un observateur O situé à une latitude φ, observant une étoile E situé dans son méridien. (Oz) désigne son zénith, l'angle ^yOz est droit. Les demi-droites [OE) et [TE') définissent la direction de l'étoile E, elles sont parallèles. Notre observateur mesure la hauteur h = ^yOE de l'étoile. La déclinaison de E est  δ = ^xTE'. Les angles ^OTE' et ^zOE ont même mesure, à savoir φ - δ. Par suite :

φ - δ + h = 90°

 !  Attention , danger : Si l'étoile est le Soleil, il s'agira de se protéger au moyen de lunettes et optiques de mesures adaptées (on trouve des caches appropriés dans les boutiques spécialisées). Des verres de lunettes de Soleil sont très insuffisants.

♦ Mesure d'une latitude et hauteur du pôle :    

La déclinaison de l'étoile polaire (la bien nommée) est très proche de 90° N, raison pour laquelle elle fut, et est encore, utilisée en mer pour le calcul de la latitude. Ci-dessous l'observateur observe l'étoile polaire que l'on peut considérée comme rejetée à l'infini dans la direction de l'axe du monde (sn) :

Les angles marqués en orange sont à côtés perpendiculaires; ils ont donc même mesure. Celui de centre T est la latitude du lieu , le second est la hauteur du pôle relative à l'observateur :

1. La latitude d'un lieu en tout point de la Terre est la hauteur du pôle céleste visible en ce lieu
(pole boréal dans l'hémisphère nord, pôle austral dans l'hémisphère sud)

➔  Dans la pratique et historiquement, l'évaluation de la latitude exposée ci-dessus était réalisée au moyen d'un quadrant (» réf.8a, Al-Khwarizmi) dont les origines sont très anciennes, ou d'un astrolabe (» réf.8b), instruments d'observation céleste remontant à Hipparque de Nicée, 150 ans avant J.-C. Puis, grâce aux instruments d'optique comme le sextant (» réf.8c,8d) inventé au 18è siècle. De nos jours, on utilise un signal GPS (Global Positioning System, » réf.6) indiquant, via les satellites géostationnaires, les coordonnées géographiques locales. En son absence, le sextant est encore en usage (désert et navigation maritime en particulier).

               
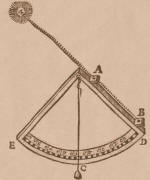
            Un quadrant                           Un sextant                    Un astrolabe XIIè siècle

♦ Mesure d'une longitude et ascension droite d'une étoile :    

L'ascension droite d'une étoile éloignée est quasiment constante au cours d'une année (comme dit précédemment, ce n'est pas le cas du Soleil). Si l'on connaît l'ascension droite d'une étoile visible en un lieu, la longitude de ce lieu correspondra à sa position culminante (donc au méridien de l'observateur). Comme pour la latitude, on pouvait autrefois utiliser un quadrant (» réf.8a) ou un astrolabe (» réf.8b).

Les astronomes grecs de l'Antiquité, dont le célèbre Ptolémée en particulier, au 2è siècle après J.-C., astronome et géographe, avaient dressé des tables de coordonnées géographiques dont les longitudes étaient basées sur un méridien origine situé aux Canaries, sur l'Île de Fer, à l'extrême ouest du monde occidental connu. Mais ces données apparurent approximatives et erronées par les astronomes arabes du Moyen-âge. Une partie d'entre elles furent corrigées plus ou moins bien par Al-Khwarizmi au 9è siècle. Cependant, en déplaçant le méridien 0 vers l'Est sur la côte africaine, il sema une grande confusion tant dans le domaine de la géographie que de l'astronomie de son époque et de ses successeurs (» réf.10-11).

» Ptolémée , Brahmagupta

Photo (perso) du ciel prise en pose au voisinage de l'étoile polaire, coin haut droit,
étoile α de la Petite Ourse, alias Polaris, proche du pôle nord céleste.

➔  Pour en savoir plus :

1. Repérage d'un astre sur la sphère céleste (coordonnées équatoriales, horaires, horizontales, écliptiques) et relations entre ces diverses coordonnées (trigonométrie sphérique) : https://cral-perso.univ-lyon1.fr/labo/fc/cdroms/docu_astro/reperage/reperage.pdf

2. a) Petite Ourse et Grande Ourse, histoire, mythologie et caractéristiques (pages Wikipedia) :
   https://fr.wikipedia.org/wiki/Petite_Ourse  |  https://fr.wikipedia.org/wiki/Grande_Ourse
   b) Déclinaison de Polaris (étoile polaire actuelle) : https://articles.adsabs.harvard.edu/full/seri/LAstr/0076//0000122.000.html

3. Précession des équinoxes (univ. du Mans) : http://ressources.univ-lemans.fr/AccesLibre/UM/Pedago/physique/02/divers/equinoxe.html

4. Solstices, équinoxes et précession : vidéo YouTube (chaine Bright Blue) :
   https://www.youtube.com/watch?v=yARKHaPmE0o

5. Institut de Mécanique Céleste et Calcul des Éphémérides (IMCCE, Observatoire de Paris) :
   a) Accueil : https://www.imcce.fr      b) Éphémérides : https://www.imcce.fr/services/ephemerides/

6. a) Global Positioning System : https://fr.wikipedia.org/wiki/Global_Positioning_System
   b) GPS, assistant de navigation : https://fr.wikipedia.org/wiki/GPS_(assistant_de_navigation)
   c) GALILEO (système de positionnement) : https://fr.wikipedia.org/wiki/Galileo_(système_de_positionnement)

7. a) La langue des mathématiques en arabe, par Mohamed Souissi (univ. Tunis), 1968.
   b) Biographie de Abu Ali al-Hasan ben Ali ben Ibrahim al-Qattan  al-Marwazi, astronome originaire de Marw (Turkménistan) :
   https://islamsci.mcgill.ca/RASI/BEA/Qattan_al-Marwazi_BEA.htm

8. a) Les quadrants astronomiques sur Wikipédia : https://fr.wikipedia.org/wiki/Quadrant_(instrument)
   b) Histoire de l'astrolabe sur Wikipédia : https://fr.wikipedia.org/wiki/Astrolabe
   c) Le sextant sur Wikipedia : https://fr.wikipedia.org/wiki/Sextant

9. Détermination de la latitude d'un lieu terrestre à l'aide d'un sextant (plateforme ACCES, Ens Lyon) :
   http://acces.ens-lyon.fr/acces/logiciels/e-librairie/astronomie-et-science-de-lunivers/

10. Histoire des différents méridiens origine (IGN) : https://geodesie.ign.fr/contenu/fichiers/Meridiens_greenwich_paris.pdf

11. Geographical coordinates of localities in the al-Maghreb ans al-Andalus localities par Eric Mercier, univ. Nantes :
    a) https://www.raco.cat/index.php/Suhayl/article/download/377825/471181
    b) https://www.e-perimetron.org/Vol_15_2/Mercier.pdf