ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Équation paramétrée du ruban de Möbius    images d'une surface de Möbius

Un cylindre peut s'interpréter dans un repère orthonormé (O, Ox, Oy, Oz) comme une surface réglée obtenue par la rotation autour de O du milieu H d'un segment restant perpendiculaire au plan (xOy).

Par suite, le ruban de Möbius s'interprétera de façon semblable avec la condition que notre segment fasse, au cours de la rotation de H autour de O, un demi-tour autour de H.

Avec les notations de la figure :

• K désigne la projection orthogonale d'un point M du segment sur le plan (xOy), plan de rotation de H;

• r le rayon du cercle;

• v l'angle orienté (Ox,OH);

• OH = r , HK = u.cost.

La cote de M est  z_M = KM = u.sint.

Animation de cette génération du ruban sur YouTube :

L'abscisse et l'ordonnée de M sont donnés par la projection de sur (Ox) et (Oy) :

 x_M = OK.cosv ,  y_M = OK.sinv

L'angle v varie entre 0 et 2p ou tout autre intervalle d'amplitude 2p. Pour que notre segment se retourne, en revenant à sa position initiale au bout d'un tour, l'angle t variera de +p/2 à -p/2. Décidons alors de faire varier v de +p à -p : c'est dire que t = v/2.

Quant à u, c'est un paramètre fixant en fait la mesure du segment que doit décrire M au cours de la rotation : décidons qu'il variera de 1 à -1 (une unité au-dessus ou au-dessous de H).

Finalement, l'équation du ruban est :

On pourra préférer écrire, en faisant varier v de 0 à p :

x = (r + u.cosv).cos2v, y = (r + u.cosv).sin2v, z = u.sinv

Avec r = 2, voici le ruban de Möbius obtenu au moyen du logiciel Surface2 de Denis Monasse :

Si vous fabriquez un ruban de Möbius en retournant une seconde fois la bande avant de la coller, vous obtiendrez une surface orientable. L'équation correspondante sera (v/2 devient v pour simuler un tour complet de la génératrice) :

x = (r + u.cosv).cosv, y = (r + u.cosv).sinv, z = u.sinv

On remarquera que le bord du ruban peut être tracé dans le même logiciel en fixant u à 1 (ou bien -1). La courbe, fermée, sans point double, est homéomorphe à un cercle de rayon 2r (longueur 22πr) :

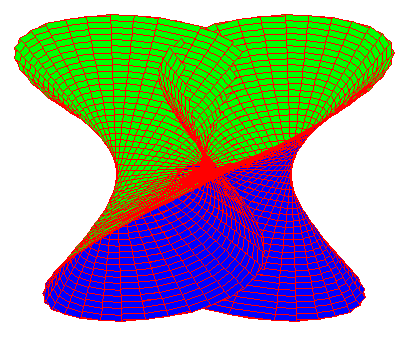
Si une droite remplace le segment, on obtient cette très belle surface réglée montrée ci-dessous sous deux points de vue :

L'équation de la surface est de la forme (u,v)j(u,v) = f(v) + u.D(v) = (r.cosv, r.sinv, 0) + u.(cos(v/2)cosv, cos(v/2)sinv, sin(v/2)), u décrivant R et v variant de 0 à 2p : il s'agit donc bien d'une surface réglée. Cette surface n'est pas développable, ni le ruban de Möbius (contrairement à ce que l'on pourrait croire), car la courbure totale de la surface n'est pas nulle, la torsion y est forte.

Rappelons que la confection en papier du ruban n'est qu'une approximation de l'objet mathématique rendant seulement compte de l'impossibilité d'orienter la surface et n'est réalisable que si le rapport de la longueur à la largeur de la bande est supérieure à 3. Sinon, déchirure, à moins que la bande ne se traverse elle-même : c'est la surface ci-dessus et dessous...

Et si on recolle après un tour complet :