ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
WHITNEY Hassler,
américain, 1907-1989 |
Éléments biographiques :
A first course in graph theory (Google Livres).
Portrait :
Wolf Foundation.
Hassler Whitney étudia à Harvard (Cambridge USA) où il obtint son doctorat (1932) portant sur la théorie des graphes sous la direction de George Birkhoff (» réf.5). Il fut professeur à Harvard jusqu'en 1952 puis à Princeton au renommé Institute for Advanced Study.
Ses travaux ont principalement porté sur la géométrie différentielle et la géométrie algébrique où il donne une première définition générale du concept d'espace fibré dans un article intitulé Differentiable manifolds (Variétés différentiables) publié en 1936, suivi de Topological properties of differentiable manifolds (1937). Cependant, Sans être formalisée, la notion d'espace fibré (Faberraum) avait été utilisée au début des années 1930 principalement par les allemands Karl Seifert et Heinz Hopf dans leurs travaux en topologie algébrique.
Whitney reçut le prix Wolf 1982 pour ses travaux fondamentaux en topologie algébrique, géométrie et topologie différentielles, ainsi que le prix Steele 1985.
|
Le concept d'espace fibré : |
Il s'agit là d'un sujet ardu méritant une rigueur et une précision de langage dont le développement nécessite de solides prérequis tout en géométrie algébrique et différentielle. Il serait donc vain d'en donner une définition dans le cadre de ce site et de ses objectifs. Jean Dieudonné en décrit la genèse dans son History of algebraic and differential topology (» réf.1) :
Traduction des 1er et 2nd paragraphes :
♦ Le concept de fibration prend sa source dans le cadre de champs de vecteurs ou de repère mobile sur une variété différentielle X; ils traitent de ce qui peut être considéré comme une sorte de fonction définie sur X, mais qui, pour chaque x, prend sa valeur f(x) dans un ensemble variable Ex variable avec x. Une fibration est un espace E muni d'une topologie appropriée qui, en tant qu'ensemble, est l'union disjointe des Ex lorsque x décrit X, appelés "fibres" (au-dessus de x). Une section (illustrée en orange sur le schéma)) de la fibration E est alors une application continue s : X → E telle que s(x) ∈ Ex pour chaque x de X.
♦ La 1ère définition générale était donnée par Whitney en 1935 et ses idées ont été développées un peu plus tard par Ehresmann, Feldbau et Steenrod. Le type de fibration qu'ils ont étudié est ce que l'on appelle maintenant l'espace (localement trivial) des fibres. Il est formellement défini comme un quadruplet z = (E, B, F, p) où E est l'espace total, B l'espace de base, F la fibre type et p, la projection, application p de E dans B, continue et surjective satisfaisant la condition que chaque point b de B possède un voisinage ouvert U pour lequel il existe un homéomorphisme φ de U × F sur p-1(U) satisfaisant p(φ(y,t)) = y pour tout y ∈ U et t ∈ F.
Sur ce schéma p-1(x) est la fibre au-dessus de x.
➔ On pourra consulter (» réf.2) un cours extrêmement de riche sur le sujet (Robert Coqueraux, univ. Marseille) dans le cadre de l'application du concept d'espace fibré à la physique quantique. On pourra aussi étudier des exemples concrets que sont la fibration de Hopf, une approche de la représentation 3D de la sphère S3 de l'espace quadridimensionnel, et le ruban de Möbius (» réf.3&4).
La notion d'espace fibré (vectoriel) par Valentin Poénaru : » La sphère S3 et la fibration de Hopf : »
|
La théorie des singularités : |
Dans ce domaine de la géométrie différentielle, le nom de Whitney est aussi attaché à d'importants résultats sur ce qu'on appelle aujourd'hui la théorie des singularités, relative aux fonctions définies sur des variétés différentielles, travaux sur lesquels René Thom s'appuiera en partie pour construire sa théorie des catastrophes.
Parapluie (ou ombrelle) de Whitney (tracé Geogebra , animation générée par WIMS) :
Il s'agit d'une surface exhibée par Whitney comme exemple de variété de R3 présentant une singularité au point O(0,0,0) : la surface admet un plan tangent en tout point sauf en O qui est un point-pince (en angliq pinch-point) dont tout voisinage "s'auto-intersecte". On parle ainsi d'auto-intersection et plus particulièrement, en l'occurrence, de singularité de Whitney ou de fronce au voisinage de ce point (par opposition à un pli).
noter que le point-pince est à une surface ce que le point de rebroussement est aux courbes planes ou gauches. On pourra consulter l'article Le pli et la fronce d'Etienne Ghys et Jos Leys faisant allusion à ce type de singularité sur le site Images des mathématiques du CNRS (» réf.5).
Cette surface s'interprète en tant que fonction différentiable de R2 dans R3 :
f(u,v) = (u,uv,v2), u et v décrivant l'intervalle [-1,1] » Gauss
La surface admet une auto-intersection tout au long du demi-axe (Oz).
➔ Étant donné une surface S, on dit que S s'auto-intersecte s'il existe une courbe de S traversée au moins deux fois par la surface. On parle d'auto-intersection. Cela signifie en particulier que la fonction f (comme ci-dessus) n'est pas injective. Le terme peut s'appliquer aux courbes du plan ou de l'espace mais on parle plutôt de point double et éventuellement de point triple, quadruple, ..., multiple.
Le parapluie de Whitney est une surface réglée dont les génératrices s'appuient sur une parabole : en effet, quitte à échanger les rôles symétriques de u et v afin de coïncider avec la page relative à ce type de surface, on peut écrire son équation sous la forme d'une famille de droites paramétrées :
(u,v) →φ(u,v) = (v,uv,u2) = (0,0,u2) + v.(1,u,0) , (u,v)∈ [-1,1]2
Δ(u) = (1,u,0) dirige les génératrices parallèles au plan (xOy) passant par les points (0,0,u2) de (Oz). Dans chaque plan "vertical" d'équation x = v, les génératrices s'appuient sur la parabole y = uv, z = u2, c'est à dire z = y2/v2.
Pour une construction "filaire" de la surface, on peut remarquer que si v = ±1, on a x = ±1 et z = y2. Dans chacun des plans verticaux x = 1 et x = -1, on construit sur une planchette deux arceaux sensiblement paraboliques d'équation z = y2. On dresse un tige T au centre de la planchette représentant le demi-axe (Oz) et on relie chaque parabole par les fils générateurs en nouant autour de T et en restant parallèles à la planchette (xOy). Et plus il y aura de fils, mieux apparaitra le pinch-point !
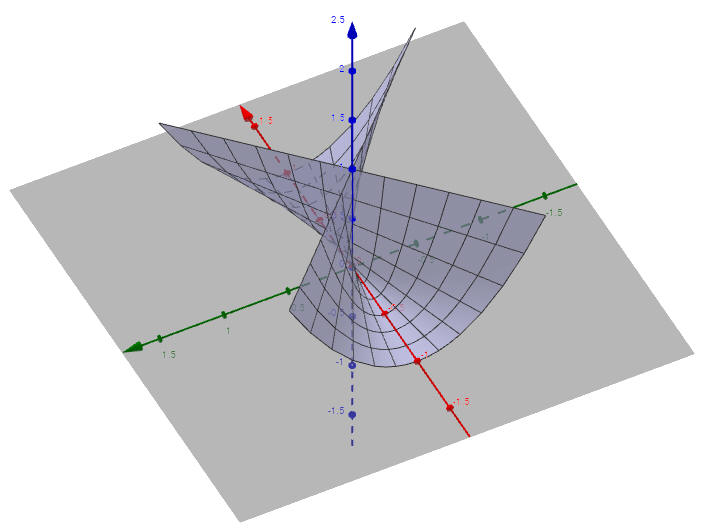
Pour mieux contempler
le pinch-point, on a ici "retourné" et rehaussé l'ombrelle par rapport au plan (xOy)
:
f(u,v) = (uv,u,-v2
+1.5),
u et v décrivant [-1,1]
Théorème du plongement (Whitney) :
Dans ce même cadre d'étude, Whitney, prolongeant des travaux de Veblen, revisite la définition des variétés en les émancipant des espaces euclidiens et établit des théorèmes de plongement et d'immersion comme :
Étant données deux variétés X et Y de dimensions finies respectives m et n telles que 2m + 1 ≤ n , alors toute application propre de X dans Y est homotope à un plongement.
Cet important résultat permet d'étudier une variété abstraite de dimension n en tant que plongement dans R2n+1.
Un théorème de Whitney :
Pour tout fermé F de Rn, il existe une fonction f de classe C∞ de Rn dans R telle que F = f -1(0).
On pourra trouver la preuve de ce théorème dans le sujet de Capes 2006 revisité par Patrice Lassère (univ. P. Sabatier, Toulouse (» réf.4 ci-dessous).
➔ Pour en savoir plus :
Représentation de l'hypersphère S3 au moyen de la fibration de Hopf,
vidéo d'Étienne Ghys, coproduction J. Leys & A. ALvarez 
Herbrand