ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Loxodromie & orthodromie     » Programme JavaScript
     Calcul du méridien terrestre : Eratosthène | Al-Biruni | Maupertuis | Méchain | Delambre | » Géodésie , Coordonnées géographiques et célestes

Considérons une surface (Σ) de révolution, d'axe (d), comme une sphère, un cylindre droit, un hyperboloïde (» surfaces usuelles). La section de cette surface par un plan contenant (d) est une méridienne de (Σ). La section de (Σ) par un plan orthogonal à (d) est un parallèle de (Σ) : ce sont des cercles.

 ➔  On remarquera qu'un cercle de centre O tracée sur la sphère est un grand cercle : son rayon est R, et qu'un cercle de rayon R tracée sur la sphère est nécessairement de centre O.

Sphère céleste, équateur céleste : »

♦ Loxodromie :   

Un chemin de (Σ) coupant les méridiennes (et les parallèles) sous un angle constant (navigation à cap constant) est une loxodromie de (Σ), du grec loxos = oblique et dromos = course.

» Les loxodromies du cylindre de révolution sont les hélices circulaires. Pour le tore, ce sont les cercles de Villarceau.

♦ Orthodromie :   

Un chemin le long d'une méridienne est dit orthodromique, du grec ortho = droit et dromeîn = courir. On parle aussi d'orthodromie. C'est un plus court chemin (s'il existe) entre deux points de (Σ), portion de géodésique de (Σ). Sur la sphère, il s'agit d'une portion de grand cercle.

» Pedro Nonius

Sur une carte géographique de Mercator, les méridiens sont représentés par des droites parallèles. Par conséquent un chemin loxodromique est un segment de droite. Un tel chemin maritime pour un navire, le plus court sur la carte et le plus simple pour la navigation, n'est pas le plus court sur l'océan.

♦ Calcul du chemin loxodromique :    

Considérons, sur le globe terrestre assimilé à une sphère de rayon 1 (ci-dessous), une route maritime loxodromique, suivant le cap non nul α : une position est déterminée par la longitude λ et la latitude φ. Si A(λ,φ) et B(λ + dλ,φ + dφ) désignent deux points infiniment proches, notons ds leur distance loxodromique se projetant en dL sur le parallèle de A.

On a :

dL = dφ.tan α , mais aussi : dL = cos φ.dλ, en tant que portion de parallèle de latitude φ, d'ouverture dλ. Par suite, entre la longitude et la latitude de tout point de la loxodromie, on a la relation différentielle : dφ/cos φ = dλ/tan α.

En intégrant, C étant une constante arbitraire :

           » primitive de 1/cosx

Le membre de gauche est bien défini pour toute latitude φ de l'intervalle ]-π/2,+ π/2[.

♦ Si φA ≠ φB : on applique la formule aux deux points A(λA,φA) et B(λB,φB). La constante C s'élimine :

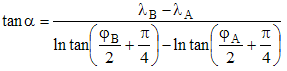       φA ≠ φB

La distance loxodromique AB est alors définie par dφ = ds.cosα, soit ds = dφ /cosα sur la sphère unité, c'est dire que pour un rayon terrestre R, le chemin loxodromique entre deux points A et B, de latitudes distinctes φA et φB, est :

♦ Si φA = φB : le problème est résolu par AB = R × cosφA × (λB - λA) car on se déplace sur un parallèle de latitude φA.

 ➔  Noter qu'un résultat AB négatif signifie qu'on se déplace vers l'ouest (longitudes décroissantes). Le programme JavaScript ci-dessous affiche les résultats en valeur absolue.

♦ Calcul du chemin orthodromique :    

Un chemin orthodromique se calcule au moyen de la trigonométrie sphérique car dans ce cas, le triangle ABN est constitué de trois arcs de grand cercle. On a :

a = π/2 - φB   ,  b = π/2 - φA  ,  ^N = λB - λA

Selon la règle des cosinus, on a :  cos n = cos a.cos b + sin a.sin b.cos ^N , soit :

cos n = sinφB.sinφA + cosφB.cosφA.cos(λB - λA)

et par conséquent, le chemin orthodromique AB est :

AB = R × Acs n     (Acs = fonction Arc cosinus, réciproque de la fonction cos)

Petit complément sur la loxodromie :    

La loxodromie s'enroule en spirale autour du pôle, point asymptote de la courbe, et dans une projection stéréographique sur le plan équatorial, deux tangentes à la sphère faisant entre elles un angle α se projettent en conservant le même angle.

Un chemin loxodromique sur une sphère se projette ainsi sur le plan équatorial en une courbe faisant un angle constant avec les méridiens projetés, donc avec tous les diamètres qui sont les projections de ces derniers : c'est une spirale équiangle, aussi appelée spirale logarithmique. C'est l'astronome Halley qui constata le premier ce résultat.

Clélies (courbes sphériques de Grandi) : »

A titre d'exemples :   

<SCRIPT LANGUAGE=JavaScript>
var pi=3.141592653589793;
function go()
{
with (Math)
{
phi_a="0";long_a="0"
phi_a=eval(prompt("Latitude de A en d° = ",phi_a))
if (phi_a==null) {return}
long_a=eval(prompt("Longitude de A en d° = ",long_a))
if (long_a==null) {return}

phi_b="60";long_b="120"
phi_b=eval(prompt("Latitude de B en d° = ",phi_b))
if (phi_b==null) {return}
long_b=eval(prompt("Longitude de B en d° = ",long_b))
if (long_b==null) {return}

rt = 6378; rt=eval(prompt("Rayon de la Terre = ",rt))
if (rt==null) {return}

delta=phi_b-phi_a;phi_a=phi_a*pi/180;long_a=long_a*pi/180
phi_b=phi_b*pi/180;long_b=long_b*pi/180
if(delta!=0)  // points de latitudes distinctes
{
tg=(long_b-long_a)/(log(tan(phi_b/2+pi/4))-log(tan(phi_a/2+pi/4)))
alpha=atan(tg);
d_loxo=rt*(phi_b-phi_a)/cos(alpha)
}
else
{
d_loxo=abs(rt*cos(phi_a)*(long_b-long_a))
}
cos_n=sin(phi_a)*sin(phi_b)+cos(phi_a)*cos(phi_b)*cos(long_b-long_a)
d_ortho=abs(rt*acos(cos_n));ortho = arr(d_ortho);loxo=arr(d_loxo)
alert("Distance loxodromique = "+loxo+"\n"+"Distance orthodromique = "+ortho)
}
function arr(x)   // arrondi à l'entier le plus proche
 {
 u=Math.floor(x+0.5)
 return u
 }
}
</SCRIPT>

© Serge Mehl - www.chronomath.com