
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
 |
La sextique de Cayley est la podaire de la cardioïde par rapport à son point de rebroussement. Elle fut en fait étudiée auparavant par Maclaurin et Cayley s'en "empara" pour la présenter en tant que courbe algébrique du 6ème degré. C'est une courbe algébrique de degré 6, d'où son nom.
Étudions-là tout d'abord géométriquement en considérant l'animation ci-dessous : la courbe est le lieu géométrique de P, pied de la perpendiculaire abaissée sur la tangente en M à la courbe depuis son point de rebroussement A. La tangente en M est obtenue comme perpendiculaire à (TM), normale en M car T est le centre instantané de rotation de chaque point M (»
trochoïdes). Pour la construction de la cardioïde, on pourra se référer à :

Cardioïde en tant qu'épicycloïde : »
Génération :
La sextique est générée ci-dessous au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :


| Équation paramétrique de la sextique : |
Nous partons de l'équation d'une cardioïde lorsque r = 1 en ajoutant 1 à x de sorte que l'origine des coordonnées soit au point de rebroussement A de la cardioïde. Choisissons alors :
x = cos2t - 2cost + 1 , y = sint2t - 2sint
Il nous suffit alors d'appliquer les formules de l'équation d'une podaire par rapport à l'origine des coordonnées :

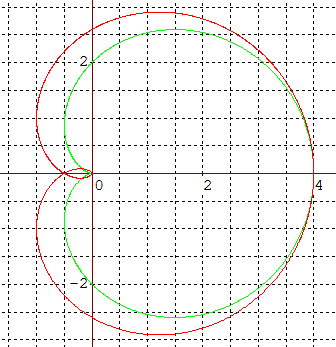
Ci-dessus, la cardioïde est tracée en
vert, sa podaire en
rouge
On trouve sans difficulté aucune : n
2 = 8(1 - cost) car dans le calcul on rencontrecost.cos2t + sint.sin2t = cos(t - 2t) = cos(-t) = cost
On calcule ensuite d = 2cos2t - 6(costcos2t + sintsin2t) - 2cost + 6 = 2cos2t - 8cost + 6 = 4cos2t - 8cost + 4.
Par conséquent d = 4(cost - 1)2. D'où d/n2 = ½(1 - cost).
Ces calculs conduisent à l'équation paramétrique de notre podaire :
X = (1 - cost)(cos2t - cost) = (1 - cost)(2cos2t
- cost - 1) = (1 - cost)(cost - 1)(2cost + 1)
X = - (1 - cost)2(2cost + 1) =
- 4sin4(t/2)(2cost
+ 1).
Pour éviter le signe négatif devant la parenthèse, on peut poser t =
π - u, on obtient : X = 4cos4(t/2)(2cost
- 1)
Y= (1 - cost)(sin2t - sint).
Ce qui peut aussi s'écrire Y = 2sin2(t/2) × 2cos(3t/2)sin(t/2)
»
formules de Simpson
D'où une autre écriture : Y = 4sin3(t/2)cos(3t/2).
Finalement : X = 4cos4(t/2)(2cost - 1) , Y = 4sin3(t/2)cos(3t/2).
| Équation cartésienne de la sextique de Cayley : |
On a X2 + Y2 = d2/n2 = 2(1 - cost)3. Or X2 + Y2 - X = 2(1 - cost)3 + (1 - cost)2(2cost + 1) = 3(1 - cost)3. Élevons au cube : nous obtenons 27(1 - cost)6 = 2(1 - cost)3 = 27(X2 + Y)/4.
Cette manip conduit à une équation cartésienne de la forme :
4(X2 + Y2 - X)3 = 27( X2 + Y2)2
Ce qui montre que la podaire de la cardioïde est une sextique : courbe algébrique de degré 6. C'est aussi le cas de la néphroïde dont cette courbe est d'ailleurs la développée : on le montrera facilement. La sextique de Cayley est aussi l'inverse de la courbe de Tschirnhausen par rapport à son foyer.

| Équation polaire de la sextique : |
Le rayon vecteur est ρ = AP. Posons u = ^(Ax, AT). M décrit la cardioïde et on a selon le calcul explicité sur la page qui lui est consacrée : AM = 4rcos
2(u). Le triangle AMP est rectangle en P et AP = ρ = AM × cos^MAP = AM × cosu. Par conséquent, ρ = 4rcos3(u). Mais ^(Ax, AP) = t, donc u = t/3 et :ρ = 4rcos
3(t/3)! Là encore, comme dit à la page cardioïde, il ne fallait pas chercher à calculer ρ au moyen de ρ2 = x2 + y2 avec X = - 4sin4(t/2)(2cost + 1) , Y = 4sin3(t/2)cos(3t/2). D'ailleurs, on peut constater plus simplement qu'avec les notations précédentes, on a X2 + Y2 = d2/n2 = 2(1 - cost)3 = 16sin6(t/2), ce qui donnerait ρ = ± 4sin3(t/2) et qu'une partie de la courbe : on perd la petite boucle...