
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 |
|
Voici un programme de construction :
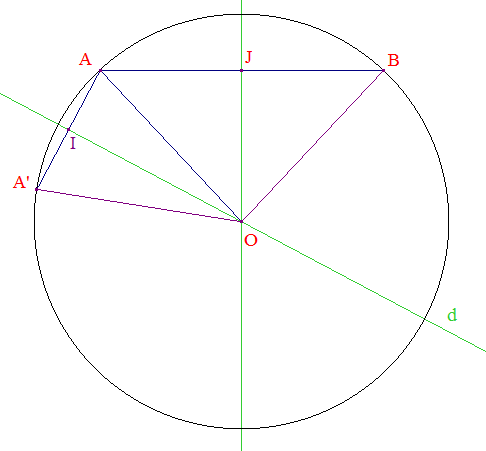
Vers le centre de la feuille, trace en oblique et en vert une droite d;
Trace un segment [AB] de 7 cm, « au-dessus » de d et parallèle au bord supérieur de la feuille;
![]()
Place le symétrique de A par rapport à d. Appelle-le A', trace le segment [AA'] et place son milieu I;
Trace en vert, en utilisant la règle et le compas, la médiatrice de [AB]; elle coupe d en O; Tu appelleras J le milieu de [AB];
Trace le cercle de centre O passant par A;
Vérifier la figure : ››››
1. Que constates-tu ? Explique pourquoi !
2. Que constates-tu ?
Explique pourquoi !
| Réponses : |
Voici la figure générée au moyen du logiciel de géométrie dynamique Cabri Géomètre :
La même figure générée CabriJava pour Internet dans sa version dynamique :

Si ton navigateur accepte les applets Java
(»
extension CheerpJ![]() ) :
) :
Tu
peux déformer la figure en déplaçant la droite d, et les points A et B
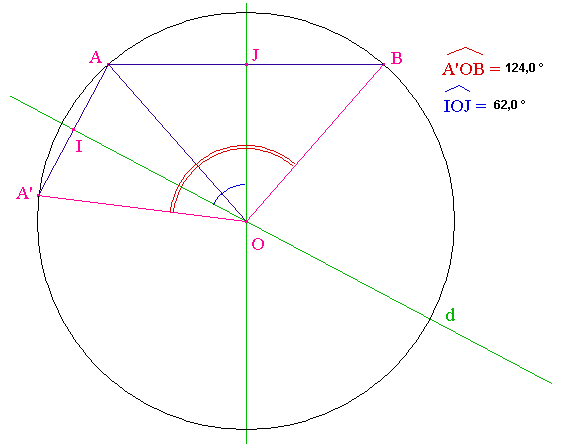
♦ 1. On constate que le cercle de centre O passant par A passe aussi par B et A' car O est à la fois :
et l'on sait que tout point situé sur la médiatrice d'un segment est à égale distance de ses extrémités :
OA = OB et OA = OA' , donc OA = OA' = OB
♦ 2. En mesurant soigneusement les angles ^A'OB et ^IOJ, on constate que ^A'OB = 2 x ^IOJ. Cela s'explique par le fait que, par symétrie (conservation des angles) :
[OI) est la bissectrice de ^AOA' : donc ^AOI = ^A'OI;
[OJ) est la bissectrice de ^AOB : donc ^AOJ = ^BOJ.
➔ Remarques :
Suivant l'inclinaison de d, les mesures des angles ci-dessus changent ! ce qui reste vrai, c'est la relation ^A'OB = 2 x ^IOJ. Tu peux vérifier cela en "déplaçant" d sur la figure dynamique
Si tu déplaces "horizontalement"
le segment [AB], sans changer sa mesure, les mesures des angles restent
invariantes.
En effet
^IOJ garde
alors la même valeur puisque d est invariante et (OJ) reste "verticale".