ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 Nature et
polyèdres, structure des minéraux
»
polyèdres |
On rencontre dans la nature des formes géométriques complexes : ce sont les réseaux cristallins de certains minéraux. Ils furent étudiés avec précision dès le 18è siècle par l'abbé René Just Haüt, minéralogiste français (1743-1822) considéré comme le "père" de la cristallographie, puis par le physicien, astronome et minéralogiste Auguste Bravais (1811-1863).
Les propriétés de symétrie et la cohérence de leur structure impliquent, de par l'agencement des atomes, la notion mathématique abstraite de structure de groupe (groupes cristallographiques).
La découverte des rayons X permit, au tout début du 20è
siècle par le physicien allemand William Röntgen (1845-1923), de confirmer les propriétés géométriques des cristaux et leur
classification.
En 1915, William Laurence Bragg partage le
prix Nobel de Physique, avec son père William Henry, pour ses recherches sur les
structures cristallines et les premiers travaux sur la radiocristallographie.
La répartition des atomes d'un cristal est comparable à un
pavage
également réparti dans l'espace à partir d'un motif géométrique élémentaire (la
maille) dont les sommets sont des atomes.
La possibilité d'existence d'une structure, eu égard à ses symétries, ses rotations et conservations des symétries par translation, implique un nombre fini de combinaisons. Un ensemble de mailles obtenu par translation constitue un réseau. Il fut prouvé qu'un réseau cristallin simple (corps non composé) ne peut posséder que des symétries d'ordre 2, 3, 4 ou 6.
Ordre d'une symétrie :
On dit qu'un objet posséde une symétrie d'ordre n d'axe (d) lorsque celui-ci est globalement invariant par une rotation d'angle 2π/n autour de l'axe (d).
Le cube, par exemple, possède :
Ci-dessous à gauche : 6 axes de symétrie d'ordre 2 (dits
axes binaires)
passant par les milieux de deux arêtes opposés :
rotations d'angle π.
Ci-dessous à droite : 4 axes de symétrie d'ordre 3 (dits
axes
ternaires) passant par deux sommets opposés :
rotations d'angle
2π/3
Ci-dessous : 3 axes de symétrie d'ordre 4 (dits axes quaternaires) passant par les centres (intersections des diagonales) de deux faces opposées : rotations d'angle 2π/4 = π/2).
1. Le groupe binaire génère 6 rotations laissant le cube
globalement invariant.
2. Le groupe ternaire en génère 8 (d'angles 2π/3 et 2π/3 + 2π/3 ≡
- 2π/3 pour chaque axe)
3. Le groupe quaternaire 9 (d'angles π/2, 2π/2 = π et 3π/2 ≡ - π/2 pour
chaque axe).
Finalement, en ajoutant l'application identique, cela nous conduit à 24 rotations laissant le cube globalement invariant. Le cube possède en outre un centre de symétrie et 9 plans de symétrie que l'on précisera aisément.
Lemme :
Le cube admet 48 isométries le laissant globalement invariant.
Preuve : ce nombre de 48 peut s'obtenir par un calcul combinatoire élémentaire : en tant qu'application affine, une isométrie est entièrement déterminée par l'image d'un repère du plan. Or, un sommet S du cube et l'angle polyèdre en ce sommet définissent un repère de l'espace (S,u,v,w). Soit f une isométrie laissant le cube globalement invariant.
à S on peut associer un des 8 sommets du cube (f peut être l'application identique) muni de son angle polyèdre et il y a 3! = 6 façons de faire cela en permutant les images de u, v et w. D'où 8 x 6 = 48 possibilités.
L'ensemble des 24 rotations constitue un groupe pour la loi de composition des applications généralement noté G+. La symétrie centrale S de centre O, centre du cube, est un antidéplacement conservant le cube. Toute isométrie R o S est un antidéplacement laissant le cube globalement invariant. S étant involutive, l'égalité R o S = R' o S implique R = R'. Le cube admet donc au moins 24 antidéplacements le laissant globalement invariant. Le nombre d'isométries étant de 48, le nombre d'antidéplacements est donc de 24 exactement.
➔ Un objet 2D ou 3D peut posséder des axes de symétrie sans pour autant posséder un centre de symétrie : c'est le cas du triangle équilatéral dans le plan et du tétraèdre régulier dans l'espace, bien que l'on parle souvent (dangereusement...) du centre de ces objets au sens du centre de gravité situé à égale distance des sommets. Si un objet possède plusieurs axes de symétrie, alors ils sont sécants et tout candidat au titre de centre de symétrie est situé à leur intersection.
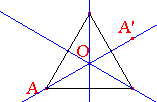
! Rappelons que le triangle équilatéral (contrairement à une croyance répandue au collège...) n'a pas de centre de symétrie : ne pas confondre avec son centre de gravité, intersection commune de ses médianes et médiatrices qui sont ses axes de symétrie. Si le point O est le centre de symétrie du triangle équilatéral, alors le symétrique A' du sommet A par rapport à O doit être un point du triangle. Ce n'est clairement pas le cas !
Classement des différentes structures cristallines :
La théorie dénombre 32 groupes possibles
que l'on peut ramener à 7 systèmes
effectivement existants, classés selon l'angle trièdre
de base formés par 4 atomes définissant un
polyèdre de base et, par là, les éléments
de symétrie et les formes dérivées.
|
|
|
|
|
Le système cubique |
cube |
la galène |
|
Le système quadratique |
prisme droit à base carrée |
zircon |
|
Le système orthorhombique |
prisme droit à base rectangulaire |
barytine |
|
Le système rhomboédrique |
rhomboèdre |
quartz |
|
Le système monoclinique |
parallélépipède incliné dont seul un angle du trièdre de base n'est pas droit |
gypse |
|
Le système triclinique |
parallélépipède incliné dont les trois angles du trièdre de base ne sont pas droits |
turquoise |
|
Le système hexagonal |
prisme droit à base hexagonal |
Aragonite |
|
|
|
Ci-dessus à gauche, le dodécaèdre
rhombique.
» en grec, rhombos
= losange. Le rhomboèdre, à droite, est un
polyèdre possédant six faces losanges
identiques. Il ressemble à un cube "incliné" et se retrouve, avec l'octaèdre principalement, dans la structure de
certains diamants.
Polyèdres réguliers (dits de Platon) : » Polyèdres archimédiens : »
➔ Pour en savoir plus :
