ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Orthocentre & cercle circonscrit           TD niveau 4ème/2nde

On se propose de prouver le résultat suivant :

Dans un triangle, les symétriques de l'orthocentre par rapport à chacun des côtés est situé sur le cercle circonscrit. On peut prouver ce résultat au moyen du concept d'homothétie (niveau 1èreS) : » cercle d'Euler.

Rappel :  

1. Les trois hauteurs d'un triangle sont concourantes (se croisent en un même point) appelé orthocentre du triangle (point H ci-dessus. Si un angle est obtus, l'orthocentre est à l'extérieur du triangle.   » Archimède

2. Si [AA'] est un diamètre d'un cercle (c) et M un point de (c) autre que A et A', alors le triangle AMA' est rectangle en M. En d'autres termes : les droites (MA) et (MA') sont perpendiculaires;

3. Si deux droites (d1) et (d2) sont perpendiculaires à une même droite (d) alors (d1) // (d2).
4. Propriété réciproque de la droite des milieux : dans un triangle ABC, une droite passant par le milieu d'un côté et parallèle à un second côté passe par le milieu du troisième côté.   » droite des milieux

Si votre navigateur accepte les applets Java (» extension CheerpJ) :
On peut déplacer les sommets du triangle ABC afin d'obtenir H extérieur ou intérieur au triangle

Problème :  

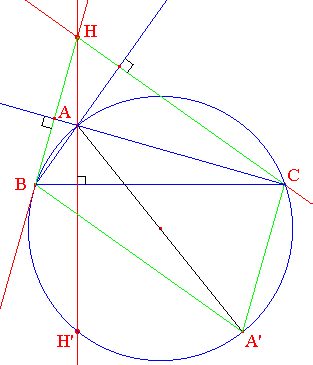
On considère un triangle ABC et son cercle circonscrit (c). On note H l'orthocentre du triangle. Démontrer que le symétrique H' de ce point par rapport au côté [BC] est situé sur (c).

Indications :  

Observez la figure ci-dessus : A' est le point diamétralement opposé à A. I est le milieu de [BC]. On s'intéresse à la hauteur (AH) qui recoupe le cercle en H'. Il s'agit de prouver que ce point n'est autre que le symétrique de H par rapport à [BC].

a/ Prouver que le quadrilatère BHCA' est un parallélogramme; En déduire que le milieu I de [BC] est aussi celui de [HA'].

b/ Justifier que (BC) et (H'A') sont parallèles.

c/ Prouver que (BC) coupe le segment [HH'] en son milieu. Conclure !

Le raisonnement semble avoir utilisé le fait que le triangle ABC est acutangle (pas d'angle obtus).
Étudier la figure ci-dessous afin de vérifier que le résultat est encore valable.

Giulio Fagnano et le triangle orthique : ››››