ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Rayon de la Lune &
distance Terre-Lune
selon Aristarque |
La Lune, on le sait, est l'unique satellite de notre planète. La Terre "tournant" autour du Soleil et la Lune "tournant" autour de la Terre, il peut advenir que l'ombre de la Terre plonge la Lune dans l'obscurité : il y a éclipse de Lune (fig.1 ci-dessus). Aristarque pensa qu'il s'agissait d'un cylindre d'ombre. En fait, malgré la distance qui nous sépare du Soleil, c'est un cône d'ombre vu l'énormité de l'astre solaire par rapport à la Terre. Aristarque évalua le diamètre du cylindre d'ombre, donc le diamètre de la Terre, à 3 diamètres lunaires. On est en fait plus proche de 4 comme nous l'allons voir. Un demi-siècle plus tard, Eratosthène améliorera les calculs.
Les
schémas relatifs à notre étude ne respectent en rien les
rapports de distances; en effet, compte tenu de la distance Terre-Soleil (@
150 000 000 km) et des 695000 km du rayon solaire, un respect approximatif de
ces rapports nécessiterait un schéma d'environ 12 m de large.
De plus, Lune et Terre ne seraient pas plus grosses qu'une
demi-tête
d'épingle...
L'orbite
de la Lune est inclinée de 5° sur l'écliptique
(plan de révolution de notre planète autour du Soleil)
et son plan subit des perturbations périodiques dues au
Soleil. Une éclipse ne peut se produire que lorsque l'orbite
de la Lune rencontre le
plan de l'écliptique (les deux points
possibles s'appellent les nœuds), ce qui explique le terme écliptique, et que la Terre se trouve alors
"alignée" avec le Soleil et la Lune, entre ces deux astres.
Si
la Lune se trouve entre le Soleil et la Terre, il y a une
éclipse de Soleil (fig.
3). Ces conditions pour les
éclipses se retrouvent périodiquement : 2 à 7
par an tous les 18 ans et 11 jours. Cette période, le
saros, fut découverte bien avant les Grecs par les
Chaldéens, ancêtres des Babyloniens,
environ 1000 ans av. J.-C. Deux éclipses totales de Lune,
visibles en France, ont eu lieu récemment en France les 21
janvier 2000 et 9 janvier 2001.
Le premier astronome de
l'Antiquité ayant établi une théorie de la Lune
susceptible de prévoir rationnellement les éclipses,
fut Ptolémée.
Une éclipse totale de Soleil fut visible le 11 août 1999
: 
Thalès.
Nous allons calculer une approximation de la distance Terre-Lune, par
une méthode proche de celle d'Aristarque
basée sur l'observation et les connaissances suivantes
:
Eratosthène.
Une
éclipse totale de Lune dure au plus 1h 45' pour une
durée de révolution autour de la terre de 29j 12h 44'.
On admettra alors que lors de l'éclipse, dans un laps de temps
aussi court, la trajectoire lunaire est
sensiblement
linéaire.
Notons RS le rayon du Soleil, RL celui de la Lune et d la distance parcourue par la Lune dans l'ombre de la Terre lors d'une éclipse totale de durée maximale : dans ce cas le centre de la Lune rencontre l'axe du cône d'ombre : alignement des centres du Soleil, de la Terre et de la Lune.
|
Les calculs : |
Soit te le temps que met la lune à entrer dans l'ombre de la Terre et ts le temps qu'elle met à en sortir complètement; on observe que le rapport de ts à te est de l'ordre de 3,7. On en déduit :
Par suite : d/RL @ 5,4
Lors d'une éclipse totale de Soleil : alignement Terre - Lune - Soleil, on constate que le disque solaire est exactement occulté par le disque lunaire : vu de la Terre, le problème se ramène à la géométrie plane (ci-dessous) et le diamètre apparent de la Lune (que voit l'observateur) est le même que celui du Soleil. On déduit de cette observation que :
RL/RS = TL/TS
où TS désigne la distance Terre-Soleil et TL la distance Terre-Lune.
Reprenons la figure 1, schématisée géométriquement ci-dessous :
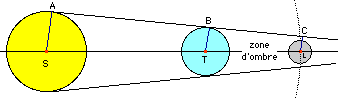
L'application du théorème de Thalès permet d'écrire :
D'où, puisque RL/RS = TL/TS : x = (RL/RS + 1)RT - RL @ RT - RL (RL étant négligeable devant RS). Par suite, vu que d @ 2x et d/RL @ 5,4 : RT @ 3,7RL , ce qui fournit
RL @ 1730 km
La Lune est vue de la Terre sous
un angle de 32 minutes : Si O désigne l'oeil d'un
observateur, l'angle ^xOy mesure 32'. La distance OL de
l'observateur au centre de la Lune est alors :
OL
= RL/tan(16') @
371704 kmOn peut donc estimer à
370 000
km la distance de la surface de la Terre à
la surface de la Lune, eu égard aux simples observations à l'œil nu.
En
fait, cette distance varie entre 360 000 km et 409 000 km du fait de la
trajectoire elliptique de la Lune autour de la Terre. Valeur moyenne : 384 500
km.
Cette
excellente approximation de la distance Terre-Lune fut établie
en 1751 par les astronomes français Joseph Jérôme
Le François de Lalande (1732-1807) et l'abbé Nicolas
Louis de La Caille (1713-1762) par une méthode de
triangulation
calculant la
parallaxe de la Lune, c'est
à dire l'angle p d'où l'on verrait, depuis le point L
de la Lune, un rayon terrestre TA ci-dessous, l'observateur
étant en A.
Triangulation , Calcul
d'une parallaxe ,
ligne d'horizon ,
Cassini