ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 ABU
(Abou) al-WAFA (Abu l'Wafa),
persan, 940-998 |
Né à Buzhgan, région du Khorasan (nord-est de
l'Iran actuel), au sein d'une famille cultivée qui l'initia aux mathématiques et
aux sciences, Abu al-Wafa,
plus précisément Abu-l-Wafa Muhammad ibn Muhammad al-Buzhgani,
également connu sous le nom de Buzjani le persan, se fit connaître à
Bagdad (Irak) en tant
qu'astronome
et mathématicien. Contemporain d'Al-Biruni,
il aurait correspondu avec ce dernier dans le cadre de leurs travaux en
astronomie. L'année précédant son décès, ils étudièrent conjointement, lui à
Bagdad, Al-Biruni à Kath (Ouzbekistan),
l'éclipse de Lune du 24 mai 997 qui leur permit dévaluer la différence de
longitude entre ces deux villes.
Carte de l'Iran et des pays frontaliers : »
Dans le domaine mathématique, Abu l'Wafa traduisit et commenta Les arithmétiques de Diophante d'Alexandrie. Il traduisit et commenta également Les Éléments d'Euclide. Ces études, ainsi que de nombreuses autres contributions sont malheureusement perdues mais on lui doit en particulier deux livres qui nous sont parvenus :
• Le Livre sur l'arithmétique nécessaire aux comptables et aux marchands où il expose différents problèmes d'arithmétique comptable et commerciale, le bon usage des unités de mesure, des formules d'aires et de volumes et une théorie élaborée du calcul fractionnaire (une fraction étant le rapport d'une quantité à une quantité supérieure) en se ramenant aux fractions unitaires et privilégiant le système sexagésimal (base 60).
• Le Livre sur les constructions géométriques nécessaires à l'artisan dans lequel il expose de subtiles méthodes de pavages et de constructions géométriques à la règle et au compas, dont certaines à ouverture constante (report de mesures).
∗∗∗
Construction
d'un triangle équilatéral inscrit dans un carré
Mais c'est en astronomie, dans son Kitab al-kamil (Le livre complet) que ses travaux sont les plus innovants dans son apport aux trigonométries plane et sphérique et l'élaboration de tables :
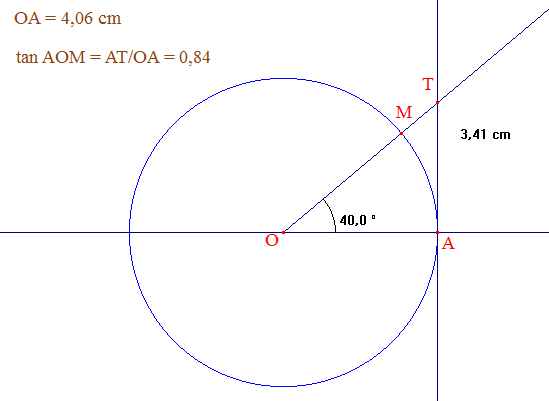
♦ La fonction tangente :
Pour faciliter les mesures d'observation et ses calculs astronomiques, on doit à Abu-l-Wafa la notion trigonométrique nouvelle de la tangente d'un angle ^AOM, figure ci-dessous : mesure du segment [AT], tangent en A au cercle de centre O, dont le rayon est pris comme unité de mesure des longueurs : cercle de rayon 1, dit aujourd'hui cercle trigonométrique lorsque le plan a été orienté.
La figure ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ
) :
Vous pouvez déplacer M ou agrandir/diminuer le cercle, ce qui a pour
effet de modifier l'unité de longueur.
Dans le triangle rectangle OTA, la tangente de l'angle ^AOT est calculée par le quotient AT/OA, ce qui revient à considérer OA comme l'unité de mesure des longueurs (cercle unité).
♦
Les
fonctions sécante et cosécante :
Abu al-Wafa est également à l'origine de la sécante et de cosécante, ainsi que des premières formules et tables de trigonométrie sphérique (initiée par Ménélaüs) indispensables au progrès de l'astronomie depuis Ptolémée.
La sécante, peu usitée de nos jours, est l'inverse de la fonction cosinus. Elle doit son nom à Frénicle de Bessy. Cette dernière fut ignorée des mathématiciens arabes, lesquels utilisèrent les demi-cordes des arcs, équivalentes au sinus pour un cercle de rayon 1 :
Ci-dessous, si le rayon OA du cercle est l'unité, OC représente le cosinus de l'angle ^AOM, OS en est le sinus. La sécante [OM) coupe la tangente en A au point T. La sécante de l'angle ^AOM est alors OT :
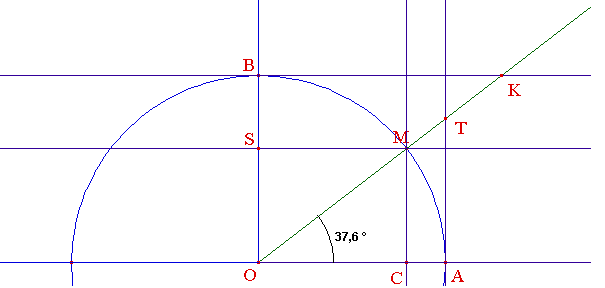
Posons x = ^AOM. En appliquant la propriété de Thalès dans le triangle OAT coupé par (MC), on voit que OA/OC = OT/OM, donc 1/cos x = 1/OT. Pa suite :
La fonction sécante : » » développement limité de la fonction sec
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ) :
Vous
pouvez déplacer les sommets A, B et C du triangle
L'abréviation sec est due à Oughtred (1657). Sur les figures ci-dessus, la sécante de l'angle â est la mesure du segment OM. Quant à la cosécante, notée cosec ou csc, elle est définie semblablement par :
La fonction cosécante : » » développement limité de la fonction csc
Sur la figure ci-dessus, il s'agit de OK. On a OB/OS = OK/OM. On voit donc que 1/sin x = OK/1, d'où la formule annoncée.
♦ Formule des sinus de la trigonométrie sphérique :
ABC désignant un triangle sphérique de rayon unité, de côtés a, b et c exprimés en distances sphériques (mesures en radians de l'arc de grand cercle correspondant à chaque côté), Abu l'Wafa prouva les égalités :
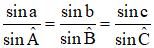
Albert Girard et la trigonométrie sphérique : » Formule des sinus en trigonométrie plane : » Mathématiques & Islam : »
➔ Sources et pour en savoir plus :
Les mathématiques arabes du 8e au 15e siècle
par Adolf P. Youschkevitch, Ed. VRIN, Paris - 1976.
La notion de fraction selon Abu l'Wafa est exposée aux pages 27 à 33,
la géométrie : 104 à 111 (principalement).
L'algèbre arabe : Genèse d'un art
Alhazen