ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

BESSEL Friedrich Wilhelm, allemand, 1784-1846

âgé de 15 ans, Bessel entre comme apprenti dans une société de commerce. Il se forme lui-même à l'astronomie et se fait connaître en présentant en 1804 un mémoire sur le calcul de la trajectoire de la comète de Halley. Dès lors, son ascension sociale est fulgurante au même titre que ses découvertes et observations célestes. On doit à cet astronome renommé, ami de Gauss, plus de 75000 observations à l'observatoire de Königsberg dont il fut le fondateur en 1812. Il fut le premier (1838) à déterminer, par le calcul de sa parallaxe, la distance de l'étoile 61 de la constellation du Cygne : environ 11 années-lumière, soit 104 000 milliards de kilomètres (1 al ≅ 9460 000 000 000 km) !

Sa contribution en mathématiques porte essentiellement sur le calcul différentiel et intégral et sur le développement en série trigonométrique des fonctions dont l'initiateur fut Fourier.

Dans l'espace vectoriel L² des fonctions de carré intégrable sur un intervalle réel [a,b], considérons un système fini de n fonctions g_i orthonormées et posons pour toute fonction f de L², les nombres :

,  i = 1,2,..., n

l'inégalité de Bessel s'écrit alors :

Σa_i² ≤ || f ||²

Dans le cas où les a_i sont les coefficients de Fourier d'une fonction numérique 2π-périodique et continue (ou tout au moins de carré intégrable), l'inégalité de Bessel devient une égalité dite de Parseval, permettant de calculer la somme de certains développements en série :

Cette égalité permet en particulier de calculer une fonction de Riemann :

Avec l'objectif de résoudre l'équation de Kepler dans le cadre du calcul des orbites planétaires, Bessel rencontra des équations différentielles linéaires du second ordre, apparentées, tout comme celles de Mathieu, à l'équation de Helmholtz. En désignant par y une fonction de la variable x réelle ou complexe, l'équation de Bessel de paramètre k (réel ou complexe) est l'équation différentielle linéaire du second ordre du type :

xy'' + y' + (x - k²/x)y = 0       (e)

Ces équations possèdent plusieurs familles de solutions.

∗∗∗
Sous réserve de convergence uniforme, on peut rechercher les solutions du type y = x^mΣu_nxⁿ, m entier relatif :
a) En remplaçant dans (e) y par x^mΣu_nxⁿ , montrer que m = ± k et u_n = u_n-2/[k² - (n + m)²].
b) On peut exprimer u_2p en fonction de u_{o et} u_2p+1 en fonction de u₁. Lorsque m = k, on choisit  u₁ = 0.
Montrer que u_2p × (-1)^p × p! × 2^2p(k + p)(k + p - 1)...(k + 1) = u_o.

Les solutions de l'équation de Bessel sont généralement notées J_k. Vérifier alors que si l'on choisit convenablement u_o, on a :

     avec 1/u_o = 2kΓ(k + 1)        »  fonction Γ

Si k est un entier naturel on a Γ(k) = k!, ce qui conduit à :

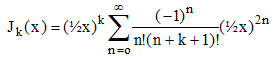
Les J_k, k entier, dites fonctions de Bessel de 1ère espèce, vérifient la récurrence :

xJ'_k = kJ_k - xJ_k+1

Elles interviennent dans de nombreux développements en série et possèdent une foule de propriétés. Des tables existent permettant d'utiliser J_o, J₁, J₂, ... en fonction de x sans faire de calculs. On a, en particulier :

» Généralement, on utilise traditionnellement la notation J_ν (lettre grecque n : prononcer nu) plutôt que J_k.

Voici quelques formules usuelles lorsque k est entier :

•  J_-k = (-1)^kJ_k ,  xJ'_k = -kJ_k + xJ_k-1   ,    xJ_k-1 +  xJ_k+1 = 2kJ_k   ,  (x^kJ_k)' = x^kJ_k-1  ,  (x^-kJ_k)' = -x^-kJ_k+1

• J'_o = -J₁   ,   J'₁ = J_o - J₁/x   _,   J₂ = 2J₁/x - J_o   ,   J'₂ = 2J_o/x - (1 - 4/x²) J₁

• J₃ = (8/x² - 1) - 4J_o/x , ...

A noter aussi que pour z fixé les J_k (z) peuvent s'écrire comme les coefficients de Fourier de la fonction t → e^izsint. On montre que l'on peut en effet écrire :

 ➔  Pour en savoir plus :

1. Cours de mathématiques, par Jean Bass, Tome II, Éd. Masson, Paris - 1964.

2. Calcul infinitésimal, par Jean Dieudonné, Éd. Hermann, Paris - 1968.

3. Les fonctions de Bessel, page de S. PouJouly.

4. Tables of Integrals and Other Mathematical Data, Éd. the Macmillan company - New-York.

5. Encyclopedic Dictionary of Mathematics (2 volumes), MIT Press Cambridge (Massachusetts) et London (England), 1993.

---

Poisson  Dupin

---

© Serge Mehl - www.chronomath.com