
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 Physicien autodidacte (il fut simple télégraphiste),
Heaviside s'intéresse aux travaux de Maxwell et se spécialise en
électromagnétisme. Sur un plan pratique, il étudia les
effets d'inductance (le terme est de lui, 1886) dans la
propagation du courant électrique le long des câbles de grande longueur
(sous-marins en particulier).
Physicien autodidacte (il fut simple télégraphiste),
Heaviside s'intéresse aux travaux de Maxwell et se spécialise en
électromagnétisme. Sur un plan pratique, il étudia les
effets d'inductance (le terme est de lui, 1886) dans la
propagation du courant électrique le long des câbles de grande longueur
(sous-marins en particulier).
Dans ces travaux, on lui doit l'équation des télégraphistes. Il est aussi à l'origine (1902) de la découverte conjecturale d'une couche supérieure de l'atmosphère réfléchissant les ondes radio, confirmée en 1929 : la ionosphère.
En mathématiques, Heaviside sera, avec Gibbs, l'initiateur de l'analyse vectorielle conduisant aux définitions actuelles de produit scalaire et de produit vectoriel de deux vecteurs de l'espace (dimension 3).
En analyse fonctionnelle, il développa une méthode de calcul symbolique permettant d'exprimer plus facilement les transformées de Fourier et de Laplace et de résoudre plus facilement les équations différentielles ou aux dérivées partielles rencontrées usuellement en électricité et magnétisme (» réf. 3&4). Le sujet sera complété (en France et en particulier) par Lévy, Leray et Pierre Humbert.
» Maxwell , Grassmann , Hamilton , Clifford
Premières notions de vecteur : » La notation des vecteurs : »
| Règles de Heaviside : |
Elles concernent des méthodes de calcul d'inversion de transformées de Laplace : si f est une fonction numérique nulle en dehors de R+, sa transformée de Laplace est la fonction qui à tout nombre réel ou complexe p associe :
Pour en savoir plus sur ce sujet, on pourra consulter les pages de Claude Saint-Blanquet (univ. Nantes, » réf.1a).
| L'équation des télégraphistes (1885-87) : |
Le long d'une ligne à deux conducteurs de longueur dx parcourue par un courant de tension v, d'intensité i,
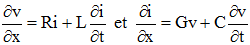 (»
réf.1)
(»
réf.1)
On peut séparer les inconnues v et i en dérivant la première équation par rapport à t et la seconde par rapport à x et en éliminant la dérivées mixtes entre les deux équations au moyen de l'égalité de Schwarz. Concernant l'intensité i, on obtient facilement l'équation aux dérivées partielles du second ordre :

En suivant le lien indiqué ci-dessus (réf.1), on trouvera une résolution de cette équation dans le cas d'un courant sinusoïdal. Henri Poincaré en donna la solution générale en 1893.
Équations aux dérivées partielles : »
| Fonction de Heaviside : |
Il s'agit de la fonction numérique, généralement notée H, de support R+ (nulle sur ]-∞,0[ ), définie par :
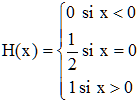
➔ Pour en savoir plus :
a) Équation des télégraphistes, par
Claude Saint-Blanquet (univ. Nantes) :
http://www.sciences.univ-nantes.fr/sites/claude_saintblanquet/synophys/335teleg/335teleg.htm
b) Règles de Heaviside :
http://www.sciences.univ-nantes.fr/physique/perso/blanquet/conducti/61laplac/61laplac.htm#3
Le calcul symbolique et ses principales applications,
par Paul Levy :
http://www.numdam.org/article/AUG_1945__21__41_0.pdf
Le calcul symbolique et ses applications à la physique
mathématique, par Pierre Humbert et Serge Colombo
http://www.numdam.org/issue/MSM_1947__105__1_0.pdf