
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

! On ne le confondra pas avec Dioclès de Carystos, médecin, chirurgien, disciple d'Aristote.
Le principal ouvrage de ce mathématicien fut transmis à l'Occident grâce aux traductions arabes. Dioclès y étudie les propriétés focales de la parabole et cherche en particulier à résoudre le célèbre problème de la duplication du cube.

Ce célèbre problème antique, également appelé problème déliaque pour signifier de Délos (île et cité grecque des Cyclades) que Ménechme, 200 ans auparavant, avait également approché par l'introduction de coniques. Dioclès construisit pour cela une courbe dite duplicatrice, connue aujourd'hui sous le doux nom de cissoïde de Dioclès.
| Étude de la cissoïde de Dioclès : |
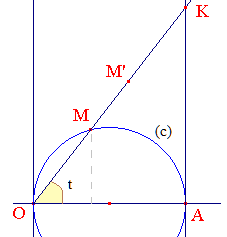
Dans un repère orthonormé, on considère un cercle (c), centré sur (Ox), milieu de OA d'abscisse a.
A tout point M de (c), autre que O, on associe le point M' ainsi défini : la demi-droite (OM] coupe la tangente en A au point K; on place alors M' tel que, vectoriellement :
On obtient ainsi une cissoïde (du grec kissos = lierre et eidos = forme) : comme on le constate sur la photo et sur l'animation ci-dessous, la courbe rappelle, en chaque concavité, et plus particulièrement auprès de la tige, la forme d'une feuille de lierre.

Équation polaire : » coordonnées polaires
Posons t = ^(OA,OM)L'équation polaire du cercle est tout simplement ici r1 = acos t = OM. l'abscisse de M est alors xM = r1cos t = acos2t et si on pose rK = OK, l'application de la propriété de Thalès conduit à :
xM/a = OM/OK, c'est à dire : acos2t/a = acos t/rK
On en déduit rK = a/cos t. Or OM' = OK - OM d'où l'équation polaire :
Équation cartésienne :
Éliminons t : on a x2 + y2 = r2 = a2(1/cos2t + cos2t - 2). Or x = r × cost = a(1 - cos2t). D'où cos2t = (a - x)/a. En remplaçant cette valeur de cos2t dans l'expression de x2 + y2, on obtient :
Il s'agit donc d'une cubique, possédant un point de rebroussement en O(0,0).
L'équation cartésienne montre qu'elle admet (OA) = (Ox) comme axe de symétrie puisque le changement de y en -y n'affecte pas la courbe. OM = r tend vers l'infini pour t tendant vers ± π/2 : comme on pouvait s'y attendre, la tangente en A au cercle est une asymptote verticale car xM' = rcost = a(1 - cos2t) tend vers a, abscisse de A.
➔ On peut étudier la courbe sous la forme | y | = f(x) que l'on obtient immédiatement à partir de (e2) : y2(a - x) = x3, fournissant :
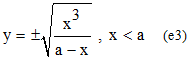
Animation :
La figure ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :


Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Pour arrêter/relancer le tracer,
clique dans la figure. Pour effacer la courbe, double-cliquer
On remarquera que la droite passant par A et N(0,2) coupe la cissoïde en un point vérifiant y = x1/3 (racine cubique de 2 : 3√2). Ce qui fournit une solution approchée du problème (ce n'est pas une construction géométrique au sens d'Euclide ou de Platon).
Cette cissoïde, dite droite car admettant un axe de symétrie (perpendiculaire à son asymptote) est un cas particulier d'une cissoïde... plus générale :
La cissoïde (cas général) : »
| Une vision nouvelle des coniques : |
D'après Pappus d'Alexandrie, à la suite des superbes résultats obtenus par Apollonius de Perge sur les sections coniques, Dioclès s'est intéressé aux coniques et aux miroirs ardents (dont le principe est attribué à Archimède) dans un contexte plus analytique et indépendamment du cône, au moyen des définitions par foyer (ce terme est de Kepler, bien plus tard) et directrice :
Étant donné un point F et une droite (d), une conique est l'ensemble des points M dont le rapport des distances à F et à (d) est constant. Une telle définition ne fournit pas le cercle.
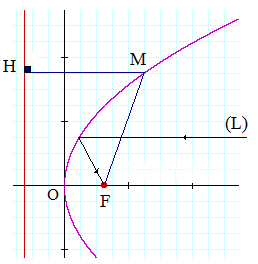
Parabole : MF/MH = 1
Ces travaux sont l'objet du livre VII de Pappus dans ses Collections mathématiques.
Les coniques : » Miroir parabolique : »