
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
» Bissectrice | Mesures (d° et grades) | Angles orientés et radians @ Programme JavaScript de conversion d°min sec / d°décimaux |
La définition d'un angle est sans doute la plus difficile à définir dans l'enseignement de la géométrie ! Elle est soit trop sommaire, soit trop subtile... Au collège, en s'appuyant sur un dessin, on peut tenter de procéder ainsi... :
Deux demi-droites [Ax) et [Ay), de même origine A, partagent un plan en deux régions définies ci-dessous par région 1 et région 2.
La région 1 correspond à un angle géométrique. Par convention, un angle géométrique ne peut pas occuper plus d'un demi-plan : ce qui correspondrait à [Ay) confondue avec [Ay''), on parle alors d'angle plat.
La région 2 correspond à un secteur angulaire : ce n'est pas un angle au sens géométrique défini ci-dessus.

On peut aussi donner la définition suivante illustrée par la figure ci-dessous :
un angle de sommet A est l'intersection de deux demi-plans de frontières distinctes (xt) et (zy) contenant A
la zone verte correspond à un angle de sommet A, les demi-droites [Ax) et [Ay) sont ses côtés.

Pour désigner un tel angle, à l'école et dans l'enseignement secondaire en général, on utilise généralement la notation due à Carnot, à savoir une écriture surmontée d'un chapeau ("grand circonflexe") :

➔
Sur
ChronoMath, pour simplifier la rédaction, on note les angles avec
un circonflexe devant le nom : ^xAy, ^A, ^ABC, ... ou
parfois "à l'américaine : ∠![]() xAy, ∠
xAy, ∠![]() A, ∠
A, ∠![]() ABC, ...ou encore, lorsque la police de caractères le permet, on écrit le
circonflexe au-dessus : Â , Ê , Î ,
Ô , Û , Ŝ
ABC, ...ou encore, lorsque la police de caractères le permet, on écrit le
circonflexe au-dessus : Â , Ê , Î ,
Ô , Û , Ŝ
➔ Notons dès à présent que ^xAy = ^yAx : il s'agit de deux objets géométriques identiques.
! Si on ne précise pas le nom des côtés, parler de ^A peut s'avérer imprécis : dans la figure ci-dessus, il y 4 angles A, même six en tenant compte des angles "plats" : ^zAy et ^xAt !
♦ Angle saillant, angle rentrant :
On parle parfois d'angle saillant pour désigner un angle géométrique (région 1) et d'angle rentrant pour désigner un secteur angulaire (région 2), mais ces termes sont aujourd'hui surannés. Le terme secteur (tout court), ou secteur circulaire, désigne une portion de disque limité par deux rayons.

Angles, vocabulaire, mesure, notations (niveau collège) : »
♦ Angle droit, angle plat, angle nul, angle aigu, angle obtus :
➔ L'angle droit, du latin directus = direct, qui a donné ligne droite au sens de "plus court chemin" sous-entendant qui n'est pas incliné. Dans le langage courant, se tenir bien droit évoque la verticalité par rapport au sol, lequel s'interprète comme un plan horizontal. On retrouve la même idée avec l'adjectif et substantif perpendiculaire qui nous vient du latin perpendiculum = fil à plomb.
à l'école et au collège, la notion d'angle droit et de perpendicularité doit rester "naturelle". Elle peut se définir intuitivement de multiples façons :
•
à partir d'une feuille de papier A4 :
rectangle ↔ quatre angles droits;
•
En partageant une galette en 4 parts
égales;
•
...
•
Lorsque [Ay) est perpendiculaire à [Ax), on dit
que l'angle ^xAy est droit.
Sur la fig.1, c'est le cas lorsque [Ay) est en
[Ay').
• Lorsque les demi-droites [Ay) et [Ax) sont
opposées, formant une droite (yx), on dit que l'angle ^xAy est
plat.
C'est la plus grande ouverture
possible pour un angle géométrique.
Sur la fig.1, c'est le cas lorsque [Ay) est en
[Ay'').
• Lorsque [Ay) est confondue avec [Ax), on dit que l'angle ^xAy est nul.
• Lorsque l'ouverture de l'angle est
inférieure à celle de l'angle droit, on dit que l'angle est
aigu.
Sur la figure 1, c'est le cas de l'angle ^xAy.
• Lorsque l'ouverture de l'angle est
supérieure à celle de l'angle droit, on dit que l'angle est
obtus.
Sur la figure 1, c'est le cas de l'angle ^xAz.
| Mesure d'un angle en degrés, minutes et secondes d'angle (ou d'arc), grade : |
Depuis, Hipparque (puis Ptolémée), on mesure l'ouverture d'un angle géométrique en degrés, terme dérivé du latin gradus = échelon, escalier sur lequel fut construit plus récemment le grade (voir ci-après).
La mesure des angles en degrés :
Par convention, un angle droit est partagé en 90 parties égales mesurant 1
degré : un angle droit mesure donc 90
degrés.
L'angle plat mesure donc 180°.
Comme pour la mesure du temps en heures, minutes et secondes, cette mesure des angles en degrés repose sur le système sexagésimal (base 60) cher aux Babyloniens : le degré d'angle se divise en 60 parties : minutes d'angle et la minute se divise en 60 parties : la seconde d'angle. On parle généralement de degré sexagesimal afin de le distinguer des degrés relatifs aux températures qui sont des nombres décimaux.
La précision des instruments augmentant au fil du temps, on peut aussi parler de tierce d'angle (un soixantième de seconde), voire de quarte, comme l'écrit Peletier du Mans dans son Arithmétique en 1549. Mais cet usage abusif de la base 60 devient alors compliqué...
Mesure angulaire d'un arc :
Étant donné un cercle de centre O, un angle saillant ^xOy définit un arc AB. La mesure de ^xOy est aussi celle de l'arc AB. On parle de degrés d'arc, minutes d'arc et secondes d'arc. Et on peut tout aussi bien considérer l'angle rentrant et l'arc associé : si on fait "un tour" de cercle complet en partant de A, on aura tourné de 360°(deux demi-tours). L'angle rentrant ^AOB mesure donc 320°.
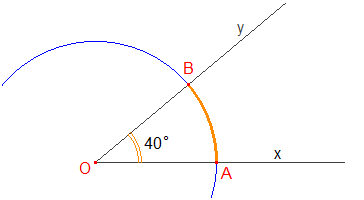 fig.4
fig.4

Du bon usage du rapporteur : »
Codage pratique des angles sur une figure géométrique :
La figure ci-dessous présente un triangle AES : comme son nom l'indique, un triangle possède trois angles : Â, Ê et Ŝ.
Deux d'entre eux, Â et Ê, possèdent un "codage".
Les petits arcs permettent d'indiquer des propriétés : l'angle  mesure 68° (68 degrés).
Un même codage indique des angles de même mesure. Le codage de l'angle Ê dans le triangle AES indique que ^AEJ = ^SEJ : la demi-droite (b) = [EJ) est la bissectrice de l'angle Ê du triangle AES.

! Parler de l'angle Ê peut s'apparenter à un redondance, car on pourrait lire l'angle angle E, tout comme parler du segment [AB] qui pourrait se lire segment segment AB, mais évitons d'ergoter...
Le codage doublé indique que ^AEJ n'est pas égal à Â.
➔ ^JES et ^SEJ indiquent le même angle : aucun ordre n'est obligatoire pour désigner les côtés : on doit cependant bien respecter le sommet ! De même, puisque S, J et A sont alignés, ^ESA et ^SEJ désignent le même angle : tout simplement l'angle Ŝ du triangle ASJ.
Quatre fiches d'exercices niveau 6ème : »
La mesure des angles en grades :
à la suite de la révolution française de 1789, l'avènement du système métrique (1801), le développement de la géodésie (mesure de la Terre par division : du grec gê = terre et daiein = diviser, » triangulation) et de la topographie (du grec topo = lieu et graphia = description), conduisirent à l'usage d'une nouvelle unité de mesure des angles : le grade, qui apparaît en 1803.
Par convention, un angle droit est dans ce
cas partagé en 100 parties égales mesurant 1 grade : un angle droit mesure
donc 100 grades.
L'angle plat mesure donc 200°. Un grade correspond donc à 9/10 de degré
(0,9 degré "décimal" : voir § suivant). On distingue ensuite les décigrades,
centigrades et milligrades. Cette nouvelle unité décimale, pourtant beaucoup
plus pratique dans les calculs n'a pas eu le succès mérité.
Remarque : dans la marine, on parle du mille marin. Si l'on considère qu'un quart de méridien terrestre mesure 10 000 km, ce qui correspond sensiblement à un rayon terrestre moyen de 6367 km (» Maupertuis), cette unité de navigation correspond à un arc de méridien de 1 centigrade, soit : (10 000 ÷ 100) ÷ 100 = 1000, c'est à dire mille mètres. En fait, le grade n'a pas été choisi pour unité ! on a préféré la définir comme longueur d'un arc de méridien de mesure 1 minute, soit (10 000 ÷ 90) ÷ 60 ≅ 1852 m.
➔ Le système décimal avec, de nos jours, l'usage des calculatrices électroniques, pourraient permettre l'abandon de la base 60. Mais une telle décision bouleverserait tant les populations que les communautés scientifiques ! On se contente de recourir au système décimal à partir des fractions de seconde d'angle (et de temps) compte tenu des nécessités scientifiques et sportives : elle se divise en dixièmes, centièmes, millièmes, etc. Par exemple : 7° 42 min 18,43 s. Et il pas interdit d'exprimer des mesures d'angle/de temps en degrés décimaux/en heures décimales. Par exemple, écrire 20,5° pour un angle de 20 degrés 30 min n'est pas illicite. (» § suivant).
| Abréviations, notations, conversion degrés décimaux/sexagésimaux et degrés/grades : |
Les abréviations pour les degrés, minutes et secondes d'angle sont deg , min et et plus symboliquement °, ' et " (» Peletier)
Les abréviations pour les grades, décigrades, centigrades et milligrades sont gr (celle du gramme, unité de poids est g), dgr (1/10è de grade), cgr (1/100è), mgr (1/1000è).
Une mesure d'angle comme 12° 18' 45'' peut être converti en degrés décimaux selon la conversion suivante :
Sachant que 1' = 1/60è de degré et 1'' = 1/60è de minute, soit 1/3600è de degré, 18' sont 18 soixantièmes de degré (18/60) et 45'' sont 45 soixantièmes de minute, soit, en degrés (45/60)/60 = 45/3600. Donc 12° 18' 45'' (sexagésimal) correspond à 12 + 18/60 + 45/3600 degrés décimaux, soit 12,3125°.
D'une façon générale, soit x la mesure d'un angle en degrés :
Si xsexagesimal = d° m' s'', alors : xdécimal = d° +m/60 + s/3600
Inversement, en notant k la partie décimale de x :
Si xdécimal = d°, k alors : xsexagesimal = d° m' s'' avec m = Ent(k × 60) et s = (k × 60 - m) × 60
La partie décimale des secondes s'exprime généralement en dixièmes ou centièmes :
Considérons par exemple 34,2796° : 0, 2796 degrés sont 0,2796 × 60 minutes, soit 16,776 minutes. Donc m = 16 et il nous reste 0,776 minutes qui représentent 0,776 × 60 = 46,56 secondes. En conclusion 34,5678° = 34° 16' 46" 56/100è.
| La mesure du temps et des températures : |
Le temps :
Depuis l'aube de l'humanité, l'écoulement du temps fut intimement lié à l'élévation du Soleil sur l'horizon, donc à un angle (» Babylone). On ne s'étonnera donc pas que le temps soit, tout comme les angles, évalué en base 60. Les abréviations pour les heures, minutes et secondes de temps sont h, min et sec (ou simplement s). On peut écrire 11 h 18 min 45 s. L'écriture aujourd'hui très utilisée est la forme 11 : 18 : 45. On notera, comme pour les angles, que parler de 1,1 heure n'est pas illicite : cela signifie 1 heure et un dixième d'heure, soit 1h 6 min.
Les températures :
Les degrés d'angle sont à distinguer bien sûr des degrés mesurant la température : les degrés Celsius (°C) et Fahrenheit (°F), du nom des physiciens suédois et allemand qui les ont définis au 18è siècle, sont les plus usités. Ces unités de température sont décimales : la température s'exprime par un nombre à virgule en base 10.
L'échelle de température de Celsius est parfois dite centésimale car elle contient 100 divisions de 0° (en deçà l'eau devient solide : glace) à 100° (au delà l'eau devient gazeuse : vapeur d'eau).
L'échelle Fahrenheit, utilisé en Grande-Bretagne et en Amérique du nord, est plus large : 0°C = 32°F et 100°C = 212°F et la correspondance °C ↔ °F est affine : °F = 1,8 × °C + 32; inversement : °C = 5/9 × (°F - 32).
Sans oublier le degré Kelvin qui devrait être le degré Lambert... C'est aujourd'hui l'unité légale de température :
Lambert et le zéro absolu (degrés Kelvin) : »

∗∗∗
Degrés C et degrés F niveau 3ème/seconde
, Angles et mesures (4 séries d'exercices #1,
#2, #3, #4)