
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
La planète P tourne uniformément autour de E tandis que E tourne uniformément autour de la Terre T :
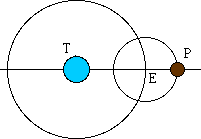
Recherchons l'équation générale de la courbe décrite par P relativement à un repère orthonormé centré en T :

En t = 0, T, E et P sont alignés, E entre T et P.
Si les vitesses angulaires de E
et P sont les mêmes, P décrit un cercle de rayon TP
et P reste aligné avec T et E.
Si la vitesse angulaire de P est
deux fois moindre que E, alors (schéma de droite) si t =
^xTE , on aura t' = ^x'EP = t/2 (il s'agit ici d'angles
orientés exprimés en radians, dans un total mais
volontaire anachronisme).
R = TE , r = EP , t' = nt avec n rationnel.
➔ Si n est non rationnel, non seulement on risque de déplaire à Hipparque et à l'harmonie du Monde prôné par Pythagore, Platon et Aristote car t et t' seraient incommensurables, mais notre planète P risque de décrire une trajectoire difficile à gérer : en théorie, elle ne se refermera pas...
En écrivant vectoriellement que TP = TE + EP, on a immédiatement l'équation de la trajectoire de P :
On peut prévoir un petit déphasage φ si, au départ, T, E et P ne sont pas alignés (nt devient nt + φ) ou si P est entre T et E (nt devient nt + π). Cette équation ressemble bigrement à celle des épitrochoïdes dites aussi épicycloïdes ...
Noter que :
• si n =
1 : P tourne dans le
même sens que E et à la même vitesse angulaire,
alors P décrit un cercle de centre T de rayon R + r.
• si n = -
1 : P tourne dans le sens rétrograde par
rapport à E mais à la même vitesse angulaire, alors P décrit une ellipse de
centre T, d'équation :
x = (R + r)cos t , y = (R - r)sin t.
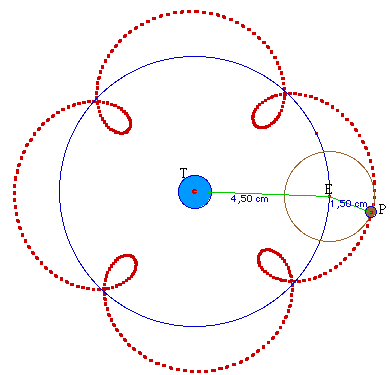
Ci-dessus, la planète P tourne sur son épicycle à une vitesse angulaire égale à quatre fois celle de E.
••• Voir l'animation :
»
© Serge Mehl -
www.chronomath.com