
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Si vous divisez 1 par 9801, abstraction faite du premier 0 et de la virgule décimale, vous obtenez comme décimales la suite des 100 premiers entiers naturels privée de 98 (en écrivant les dix premiers sous la forme 00 01 02 03 ... 08 09) :
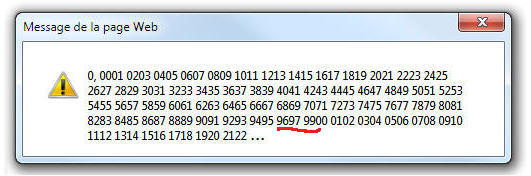
La fenêtre ci-dessus, obtenue avec ce petit programme de division, présente les 240 premières décimales et l'absence de 98 : on passe à 99 et la série reprend périodiquement, ce qui n'est pas étonnant pour un nombre rationnel. On se propose de justifier ce résultat en expliquant la perte du 98 au moyen d'un développement en série...
On peut aussi utiliser constater la perte du 98 au moyen d'un tableur (ici Microsoft Excel) :
Initialisation : en B2, on place le dividende 1, en C2 on calcule le quotient entier de de B2 par 9801.
En B3, on retire au dividende B2 le produit du quotient par 9801 et on abaisse un zéro : ce qui revient à multiplier par 10 : C'est le principe élémentaire de la division décimale.
On recopie les formules vers le bas autant que voulu.

Ce qui nous fournit :

...

La série de terme général xn , n ≥ 1, converge uniformément sur tout intervalle [0,a], 0 < a < 1. Sa limite est φ(x) = 1/(1 - x) - 1 = x/(1 - x). Il en est de même de la série dérivée de terme général nxn-1 : on majore par la série de terme général nan-1 et on applique par exemple le critère de d'Alembert, ce qui assure la convergence normale et implique la convergence uniforme.
On peut alors dériver terme à terme et écrire (» Weierstrass) :

On en déduit x2φ'(x) = x2/(1 - x)2 = [φ(x)]2, ce qui conduit à :

Choisissons alors x = 1/100 : φ(x) = 1/(1 - 1/100) - 1 = 100/99 - 1 = 1/99. Mais 9801 = 992, on est donc en droit d'écrire :

D'où 1/9801 = 0,01 × (0,01 + 0,0002 + 0,000003 + 0,00000004 + ...
Écrivons maintenant 1/9801 sous forme décimale :
1/9801 = 0, 00 01 02 03 04 05 06 07 08 09 10 11
12 ... 95 96 97 98 99 00 01 02
03...
Pourquoi le 98 est-il barré ? Nous avons :
1/9801 = 0,01 × (0,01 + 0,0002 + ... + 98/10098 + 99/10099 + 100/100/100 + ...)
= 0, 00 01 02 + ... +1/100/100 x (980000 + 9900 + 100)
= 0, 00 01 02 + ... +1/100/100 x 990000
= 0, 00 01 02 + ... +1/100/98 x 99
Ainsi, par un effet cascade de retenues, un 99 apparaît en lieu et place du 98 et on repart avec 00 01 02...

➔ Résultat semblable pour 1/998001 = 1/9992, x = 1/1000. Par tranches de 3 décimales, on obtient tous les entiers de 000 à 999 privés de 998. Und so weiter...