ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Notion de fonction, composition de fonctions    niveau collège et lycée        »  Injection, surjection, bijection | fonction composée | fonction réciproque

La notation fonctionnelle pose de nombreux problèmes au collège et au lycée. A la source de ces difficultés (classe de 3ème), la confusion entre l'écriture "parenthésée", type f(x), et l'apprentissage de la factorisation type a(bx + c) conduisant de nombreux élèves à écrire, par exemple, que si f(x) = 2x -1, alors f(3x) = 3(2x - 1) où (f o f)(x) = (2x -1)(2x - 1) ! L'objectif de cette page est de lever les ambigüités de la notation fonctionnelle.

En 1692, Leibniz met en place la notion de fonction, du latin functio = accomplissement, exécution. qui a donné fonctionnement. La fonction accomplit une action sur un objet mathématique appelé la variable car cette dernière varie...

La notation fonctionnelle initiée par Leibniz : »

On dit de quelque chose (un résultat y) qu'il dépend ou qu'il est fonction d'un truc (la variable x) si le quelque chose varie suivant les valeurs de truc.

Ces variations sont commandées (accomplies, exécutées) par un mécanisme, la fonction, que nous notons ici f. On écrira au moyen d'une fléchette ce mécanisme signifiant que x devient y :

f :  x → y 

On écrit alors, de façon plus opératoire : y = f(x) et on lit "y égale f de x"

• x est la variable de la fonction f;

• y = f(x) est l'image de x par f;

 ➔   L'usage de la lettre x pour désigner la variable est une tradition mathématique et n'est absolument pas une nécessité ! Si vous construisez vous-même une fonction, notez-la comme vous voulez, ainsi que sa (ou ses) variable(s).
Dans la définition d'une fonction, on choisit souvent la 1ère lettre du nom du résultat : par exemple g pour un gain, b pour un bénéfice. En fait, ce que vous préférerez, mais surtout pas f encore si ce nom est déjà utilisé, sinon c'est la confusion assurée !

Le fait de mettre x entre ( ) est pour signifier que f s'applique à la variable notée x. Ces ( ) ont le même rôle qu'en littérature lorsqu'il s'agit de bien instruire le lecteur sur le sens apporté à une pensée. Il ne faut nullement voir dans la présence de ce x entre parenthèses une quelconque forme de multiplication ou factorisation.

• 1/  x désignant un nombre entier, soit f la fonction définie par f(x) = 3x. Le mécanisme consiste ici à calculer le triple de x. Calculons f(4); 4 doit remplacer x dans la définition de f; d'où : f(4) = 3 × 4 = 12  (ne pas confondre x et le signe × de multiplication). Si on demande maintenant de calculer f(2x), x étant quelconque (valeur non attribuée); 2x doit remplacer x dans le mécanisme de f , laquelle s'appliquera au double de x. f(2x) = 3 × 2x = 6x.

• 2/  n désignant un nombre entier, soit f définie par f(n) = 3n - 1. Calculer f(2) et f(5n). Le mécanisme consiste ici à calculer le triple de x diminué de 1. Donc f(2) = 3 × 2 - 1 = 5. Calculons maintenant f(5n); le mécanisme s'applique à 5n et non à n seul. f(toto) = 3 × toto - 1... Donc f(5n) = 3 x 5n - 1 = 15n - 1.

• 3/ Soit x un entier. On pose y = f(x/3 +1). Calculer y lorsque x = -3. On a y = f(-3/3 - 1) = f(0) = -1.

• 4/ Soit maintenant g la fonction définie pour tout x entier par g(x) = f(x/3 +1), f étant la fonction précédente. Calculer g(x) en fonction de x. La fonction g dépend de x par l'intermédiaire de f : il s'agit alors de calculer l'image du nombre x/3 + 1 par f : g(x) = f(x/3 +1) = 3 × (x/3 +1) - 1. On a dû mettre des parenthèses car x/3 - 1 joue ici le rôle de toto... On obtient : g(x) = 3x/3 + 3 - 1, c'est à dire g(x) = x + 2.

Écrire f(x) = x² - 1/x est imprécis tant que l'ensemble dans lequel varie x ainsi que sa plage de variation n'est pas précisée.  A priori, le plus large champ de variation de x est ici R privé de 0 car la division par zéro n'a pas de sens ! f(x) est ainsi calculable sur R* = ]-∞,0[∪]0,+∞[.

Lors de l'étude d'une fonction f, il s'agit de préciser :

1. Son ensemble de départ : ensemble dans lequel la variable x de la fonction f prend ses valeurs;

2. Son ensemble d'arrivée : ensemble contenant les images f(x) de la variable;

On note f : E → F une fonction dont l'ensemble de départ est E et d'ensemble d'arrivée F.

3. Le sous-ensemble D de E constitué des éléments x ayant une image par f, est appelé ensemble de définition (ou domaine de définition). On dit que f est définie sur D.

On utilise l'expression fonction numérique pour désigner le cas f : R → R (cas de la majorité des cas étudiés au lycée). Lorsque E = N, on parle de suite numérique.   » notion de suite

• L'énoncé : "soit g la fonction numérique définie pour tout x au moins égal à 1 par g(x) = 1/x" exprime que l'ensemble de définition de g est l'intervalle D = [1,+∞[ .

• L'énoncé : "soit h : R → R, h(x) = x/sinx" ne précise pas l'ensemble de définition inclus dans R. h(x) n'a de sens que lorsque sinx est non nul. Or sinx = 0 si et seulement si x est non multiple de π, h est donc définie sur R - {kπ, k∈Z}.

• Les énoncés "pour tout x de R⁺, soit f : x → x²- 1" et "soit f : R⁺ → R, f(x) = x² - 1" sont équivalents.

 !  L'ensemble d'arrivée F d'une fonction est souvent implicite (donné par le contexte), mais il ne faut pas confondre cet ensemble avec l'image de E par cette fonction qui est incluse dans F : par exemple, en posant pour tout nombre réel x, f(x) = sinx, on définit une fonction numérique f : R→R, mais son image se réduit à l'intervalle [-1,1].

♦ Si la fonction possède plusieurs variables, il s'agira de préciser la plage de variation de chacune comme par exemple f(x,y) = xy² - 2x/y, (x,y) ∈R × R* pour signifier que x décrit [0,+∞[ et y décrit R privé de 0.

Soit f, g et h les fonctions numériques définies pour tout x réel par :

f(x) = 2x² - 4 , g(x) = 2x - 4 , h(x) = x²

La fonction h prend le carré de la variable, la fonction g double la variable et diminue le résultat de 4.

Considérons le schéma suivant où l'on a écrit au-dessus de la flèche la fonction exercée :

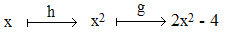
On voit qu'exercer f sur la variable x consiste à exercer h suivie de g (on applique g après h) : on prend le carré, on le double, on lui retire 4. La fonction f a été décomposée en deux actions successives :

f(x) = g(h(x)) : on dit que f est la composée de h par g et on écrit f = g o h

  !  Le petit rond (o) désigne ainsi une opération sur les fonctions : c'est la loi de composition des applications appelé parfois, dangereusement produit de composition, dangereusement car cela laisse penser à un produit comme celui de la multiplication. Le mot produit est ici utilisé pour signifier le résultat de la composition au sens de ce qui est produit par cette composition. Le petit exercice 3 ci-dessous permet de distinguer f o g et f × g.

∗∗∗
1.  Attention à l'ordre : appliquer g puis h (à savoir h o g) ne fournit pas le même résultat ! Que serait ce résultat ? ☼
2. On considère l'ensemble A des fonctions affines du type x → ax + b, a et b réels donnés.
A quelles conditions aura-t-on f o g = g o f  ? ☼

∗∗∗
3. Soit f et g les fonctions numériques définies pour tout x réel par f(x) = 2x - 4 , g(x) = x + 4
Déterminer f o g  et  f × g.  Rappel : h = f × g  (ou h  = fg) signifie h(x) = f (x) × g(x). Et, pour le plaisir, déterminer  g o f... ☼

Composée de fonctions et ensemble de définition :   

Si f et g sont des fonctions numériques d'ensembles de définition respectifs D_f et D_g, la fonction composée f o g définie par (f o g)(x) = f(g(x)) sera définie si et seulement si x∈D_g et g(x)∈D_f. Par conséquent, on peut écrire :

D_{f o g} = D_g ∩{x / g(x)∈D_f}

Sauf cas extrême, il est inutilement compliqué d'étudier les variations de g afin de rechercher l'image de g (l'ensemble des valeurs prises par g).

∗∗∗
4. Soit f et g les fonctions numériques définies par f(x) = x - 1/x , g(x) = √x.
Déterminer la fonction composée g o f en précisant son ensemble de définition.  ☼

5. On pose pour tout x distinct de 1, 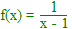. Déterminer f o f o f en précisant son ensemble de définition.☼

6. On pose pour tout x > 5, 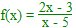et, pour tout x > 2, .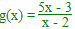
Déterminer g o f et  f o g en précisant leurs ensembles de définition. ☼
 i  on dit que f et g sont réciproques l'une de l'autre

1. Le résultat serait le carré de 2x - 4 puisqu'on appliquerait g d'abord, soit (2x - 4)². 

2. Si f(x) = ax + b et g(x) = a'x + b', alors (f o g)(x) = f(g(x)) = f(a'x + b) = a(a'x + b') + b = aa'x + ab' + b et (g o f)(x) = g(f(x)) = g(ax + b) = a'(ax + b) + b' = aa'x + a'b + b'. On aura f o g = f o g si et seulement si ab' + b = a'b + b'. La condition se ramène à b(a' - 1) = b'(a - 1).

» Les fonctions linéaires (de la forme x→ax) répondent en particulier à la question, ainsi que les fonctions affines de coefficient directeur 1. Un autre exemple : f(x) = 2x + 1 et g(x) = 4x + 3; on a f o g = f o g : x →8x + 7.

3. (f o g)(x) = f(g(x)) = f(x + 4) = 2 × (x + 4) - 4 = 2x + 4;
    (g o f)(x) = g(f(x)) = g(2x - 4) = (2x - 4) + 4 = 2x;
    (f × g)(x) = f(x) × g(x) = (2x - 4) × (x + 4) = 2x² + 4x - 16. 

4. f est définie pour tout x non nul, g est définie pour tout x positif ou nul. (g o f)(x) = g( f(x) ) = g(x - 1/x), soit :

D_{g o f}  = {x∈R / x≠0 et x - 1/x ≥ 0}. En distinguant x > 0 et x < 0, on trouvera sans difficultés D_{g o f}  = ]-∞,-1[ ∪ ]1,+∞[.

5. On peut considérer f o f o f  comme étant f o (f o f ) ou bien (f o f ) o f. Choisissons la 1ère écriture en remarquant déjà que nous devons avoir x ≠ 1 et 1/(x - 1) ≠ 1, soit x distinct de 1 et de 2 :

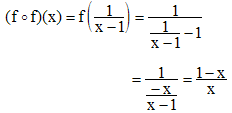
Puis, avec (1 - x)/x ≠ 1, soit x distinct de 1/2 :

Et ce, pour tout x distinct de 1/2, 1 et 2 : D_{f o f o f}  = ]-∞,1/2[ ∪ ]1/2;1[∪ ]1;2[∪ ]2,+∞[.

6. On trouvera sans difficultés (f o g)(x) = x et (g o f)(x) = x. D_{g o f} = D_f ∩{x / f(x)∈D_g}. Étant donné x > 5, il nous faut résoudre l'inéquation f(x) > 2. Mais x - 5 étant positif, on a :

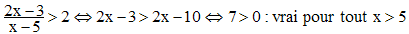
D_{g o f} =  D_f  et (g o f)(x) = x; g est donc la fonction réciproque de f. On vérifiera de même que D_{g o f} = D_g.