ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Exercices & problèmes : Applications linéaires & matrices

1.  E est de dimension 3, (i,j,k) en est une base orthonormée. Le symbole ∧désignant le produit vectoriel, pour tout v de E, on pose :

f(v) = (i ∧v) ∧i

Montrer que f est une application linéaire; préciser son noyau et son image.

»  Repère orthonormé , Produit vectoriel

2.   !  deux applications linéaires distinctes peuvent avoir même noyau et même image !

• Considérer f et k.f  lorsque k est un scalaire non nul

• Lorsque dim E = 3, considérer les endomorphismes f et g de matrices respectives dans une base B :

          voir aussi exo4

3-A E désigne un espace vectoriel de dimension au moins égale à 2 sur un corps K. Soit D un sous-espace vectoriel de E de dimension 1 (droite vectorielle). On appelle h l'application de E vers E définie par :

a/ Montrer que h(k.v) = k.h(v) pour tout k de K et tout v de E.

b/ Prouver, par un choix judicieux de v et w, que l'égalité h(v + w) = h(v) + h(w) n'est généralement pas vérifiée On dit d'une telle application n'est pas additive.

3-B Voici une application additive s'avérant linéaire :

c/ On considère deux espaces vectoriels sur le corps Q des nombres rationnels et f une application additive de E vers F, c'est à dire :

Nous allons prouver que f est linéaire :

d/ Vérifier que f(0_E) = 0_F et que pour tout v de E, f(-v) = - f(v).

e/ Prouver, par récurrence sur n, que pour tout entier naturel n et tout élément v de E :

f(n . v) = n . f(v)

f/ En remarquant que si n est un entier relatif négatif, on a n = - | n | avec (donc) | n | entier naturel, prouver que l'égalité ci-dessus se prolonge à tout n de Z.

g/ En remarquant que n/n = 1 pour tout entier relatif non nul, prouver que :

h/ En remarquant maintenant que tout rationnel q = a/b, s'écrit a × 1/b, prouver que f(q . v) = q . f(v). Conclure.

 ➔   Le résultat ci-dessus ne s'étend pas à R : on peut considérer R comme un espace vectoriel de dimension infinie sur Q et dans cet espace R, Q apparaît alors comme un sous-espace de dimension 1. On peut alors écrire R comme somme directe de Q et d'un sous-espace vectoriel V, supplémentaire de Q dans R : R = Q ⊕ V.

Par suite, tout réel x s'écrit de façon unique comme somme d'un rationnel q et d'un élément v de V : x = q + v. Considérons alors maintenant R comme espace vectoriel sur lui même et soit f l'application qui à tout x = q + v associe q :

∀ x∈R : f(x) = q  avec x = q + v

f est clairement additive mais elle ne respecte pas la loi externe de R car ici, r est de dimension 1 et par conséquent toute application linéaire est une homothétie dont on peut noter k le rapport. Or 1 est rationnel, donc d'une part f(1) = 1 et d'autre part f(1) = k.1 = k; donc k = 1 et par suite f est l'application identique : f(x) = x pour tout réel x.

Or ceci n'est pas possible car √2, par exemple, n'est pas rationnel et son image est, par définition, rationnelle, donc distincte de √2. Mais on ne connaît pas l'image de √2 : assurer l'existence de V est une chose, l'exhiber en est une autre. D'ailleurs ces lignes ne sont plus valables si vous refusez l'axiome du choix...

4.1  Un endomorphisme dont le noyau est aussi l'image :  E est un plan vectoriel rapporté à une base B = (i,j). On note f l'endomorphisme dont la matrice relativement à B, est :

i/ Vérifier que l'image de E par f est la droite vectorielle engendrée par u = i - j , dont une équation est y = -x, et qu'il en est de même du noyau.

ii/ Calculer la matrice de f o f ? Le résultat est-il surprenant ? Rép. : non !

4.2  Un endomorphisme dont le noyau est inclus strictement dans l'image : E est un espace vectoriel de dimension 3 rapporté à une base B = (i, j, k). Considérer l'endomorphisme g de E défini par g(i) = g(k) = k et g(j) = i.

4.3  Un endomorphisme dont l'image est incluse strictement dans le noyau : avec les notations ci-dessus, considérer cette fois l'endomorphisme h de E défini par h(i) = h(j) = h(k) = -2i + j + k.

5.  Étude d'un endomorphisme numérique :     

Soit E l'espace vectoriel des fonctions numériques, continues sur R et prenant la valeur zéro au point zéro. On remarque que E contient le sous-espace P des polynômes nuls en zéro dont une base est (e₁, e₂, ..., e_n, ...) où e_n désigne le monôme défini par e_n(x) = xⁿ , n∈N. P est donc de dimension infinie et par conséquent E aussi.

Pour tout f de E, on note F la primitive de f, nulle en 0 :  F(x) = et on pose h(f) = F.

1/ Montrer que h est un endomorphisme de E.

2/ On note θ la fonction nulle; c'est un élément de E. En étudiant l'équation h(f) = θ, montrer que le noyau de h est réduit à {θ} : h est donc injective.

3/ On suppose alors que h est aussi surjective : cela signifierait que toute fonction continue sur R et nulle en zéro est primitive d'une telle fonction; or ceci est faux : considérer f définie par f(x) = | x |, valeur absolue de x.  

6a.  Projection vectorielle plane :             » notion générale de projecteur

Rappel :    

Dans un espace vectoriel E, on appelle projecteur (ou projection vectorielle) un endomorphisme π tel que π o π = π. On parle d'endomorphisme idempotent car ses puissances, au sens de la loi o, sont toutes égales à π.    » idempotent (élément).

1/  !  Une application idempotente n'est pas nécessairement linéaire : vérifier que x → |x| de R dans lui-même et l'application vectorielle du plan f : v(x,y) → v(|x|,y) sont idempotentes non linéaires.

2/ Il est clair que l'application identique id_E : v → v vérifie id_E o id_E  = id_E. Montrer que le seul endomorphisme bijectif idempotent de E est l'application identique id_E : » voir cet exercice.

 ➔  Dans toute la suite, π désigne un projecteur distinct de id_E.

3/ On suppose E de dimension 2 (plan vectoriel). Montrer que la matrice M d'un projecteur π relativement à une base (i,j) de E, est de la forme :

4/ Montrer que l'ensemble des vecteurs invariants par π coïncide avec Im(f).

5/ Montrer que si π n'est pas l'endomorphisme nul θ, alors il existe une base (u,v) dans laquelle la matrice de π s'écrit :

Il s'agit alors du projecteur de base (d) dirigée par u de direction (la droite engendrée par) v.

• L'image de π est la droite (d); c'est aussi son sous-espace invariant.
• Le noyau de π, sous-espace des vecteurs dont l'image par π est nulle, est la droite vectorielle engendrée par v.
  Si V = au + bv, p(V) = au.

5/ Montrer que l'endomorphisme f défini par sa matrice :

est un projecteur. Vérifier alors 3/ et reprendre, sur ce cas particulier, les questions 4/ et 5/.

Projection affine : »

6b.  Symétrie vectorielle :             » notion générale de symétrie vectorielle

E désigne ici un espace vectoriel sur R de dimension 2 dont une base est notée (i,j). Dans la base (i,j), la matrice de φ est de la forme :

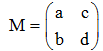
a/ Établir les relations existant entre a, b, c, et d.

b/ Montrer qu'en dehors des cas φ = ± id_E , f admet une droite vectorielle de vecteurs invariants dont on donnera un vecteur directeur u et une droite vectorielle de vecteurs changés en leur opposé dont on donnera un vecteur directeur v.

c/ Vérifier que (u,v) est une base de E et donner la matrice de φ dans cette base.

d/ Vérifier les calculs précédents dans les cas i/ a = d =  0, b = 2  et ii/ a = - d = 2, b = - c = √3

Réponses :   

a/ On a M² = I, matrice unité. Ce qui mène à 4 équations : a² + bc = 1, c(a + d) = 0, b(a + d) = 0 et d² + bc = 1.

• Supposons a ≠ - d; on a alors b = c = 0, a² = d² = 1 : le cas a = d = 1 conduit à φ = id_E ; le cas a = d = -1 conduit à φ = -id_E.

• Supposons a = - d; sous cette condition, le système se résume alors à a² + bc = 1 :

b/ φ(v) = v ⇔ Mv = v, ce qui fournit le système linéaire :

(a - 1)x + cy = 0
bx - (a + 1)y = 0.

Le déterminant est D = 1 - (a² + bc) = 0. Les deux équations de ce système homogènes sont donc proportionnelles et définissent en général une droite vectorielle. Discussion : si a = 1, alors bc = 0, c peut être nul, on choisit alors l'équation bx - 2y = 0. Si a ≠ 1, on choisit l'équation (a - 1)x + cy = 0. Relativement à la base (i,j), on prendra  :

u(2;b) si a = 1 et u(-c;a - 1) si a ≠ 1

φ(v) = -v ⇔ Mv = -v :

(a + 1)x + cy = 0
bx - (a - 1)y = 0.       Là encore, le déterminant est nul.

De manière analogue au cas précédent, suivant que a = 1 ou non : relativement à la base (i,j), on prendra :

v(-c;2) si a = 1 et v(a - 1;b) si a ≠ 1

c/ Si a = 1, on a u(2;b), v(-c;2) et bc = 0. det (u,v) = 4 ≠ 0 : u et v sont donc linéairement indépendants dans un espace de dimension 2;  ils forment donc une base de E. Si a ≠ 1, on a u(-c;a - 1), v(a - 1,b) avec a² + bc = 1. det (u,v) = 2(a - 1) ≠ 0.

Finalement, dans la base (u,v), on a u(1,0) et v(0,1) et puisque φ(u) = u et φ(v) = - v, la matrice devient :

d/ Le cas i/ implique c = 1/2 afin que φ soit involutive.

Symétrie affine : »

7. On considère les matrices 2 × 2 de la forme :

1/ Montrer que l'ensemble de ces matrices est stable pour la multiplication.
2/ Lorsque la matrice M_a est inversible, calculer son inverse.
3/ Montrer que pour tout n, on a :

8.  On considère la matrice :

Calculer M², puis M⁴, puis M⁸. En déduire M²⁰⁰⁹.

Indic. : Si I désigne la matrice  unité, vous devez constater que M4 = -I, donc M8 = (M4)2 = I. La division euclidienne de 2004 par 8 fournit : 2009 = 251 × 8 + 1. Donc  M²⁰⁰⁹ = (M⁸)²⁵¹ × M = I²⁵¹ × M = I × M = M.  » On remarquera que i est une matrice de rotation, d'angle π/4.

9. Existe-t-il des matrices carrées A d'ordre 2, non nulles, distinctes de -I (opposée de la matrice unité) et telles que A² = - A ?
Rép. : oui, par exemple : . Mais recherchez-les toutes !

Source exo : extrait inspiré de BTS informatique de gestion 1990.

10. On considère les matrices :

I est la matrice unité, élément neutre de la multiplication des matrices 3 × 3.

1°) Calculer Bⁿ pour tout entier naturel n ≥ 1 (on procédera par récurrence).

2°) Si M et N sont des matrices carrées qui commutent : M × N = N × M, alors leurs puissances commutent également et la formule du binôme de Newton s'applique à de telles matrices :

En remarquant alors que A = B + I, exprimer Aⁿ en fonction de B et I et donner l'expression matricielle de Aⁿ.

3°) Vérifier votre résultat dans le cas A².

Indic : 1°) B² = 3B = 3B¹;  B¹ = B = 3^oB. Supposons H_n : Bⁿ = 3^n-1B, n ≥ 1. Nous aurons Bⁿ⁺¹ = Bⁿ × B = 3^n-1B × B = 3^n-1B² = 3^n-1 × 3B = 3ⁿB. Par suite si H_n est vérifiée pour n ≥ 1, H_n+1 le sera également. H₁ étant vérifiée, H_n l'est également pour tout n ≥ 1.

2°) On a A = B + I. La matrice unité I commute avec toute matrice carrée 3 × 3 et toutes ses puissances sont neutres On peut alors écrire :

Quitte à mettre 1/3 en facteur, la somme du dernier membre ci-dessus ne sera autre que le développement du binôme (1 + 3)ⁿ diminué de 1, soit 4ⁿ - 1 :

Autrement dit :