
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

@ Programme de calcul en ligne | Lois binomiale & normale | Estimation par intervalles de confiance | » loi de Poisson |
Aussi appelée loi de Laplace-Gauss, la loi normale, ainsi dénommée par Pearson, au sens de naturelle, intervient dans l'étude de phénomènes quantitatifs aléatoires continus soumis à de multiples causes (aucune d'entre elles n'étant prépondérante), agissant additivement et indépendamment l'une de l'autre et dont la répartition des valeurs s'étale autour de leur moyenne.
➔ Par continu, on entend dont les valeurs peuvent être des nombres réels quelconques. Un phénomène non continu est dit discret : ses valeurs sont nombre fini ou dénombrable, c'est le cas de la loi de Poisson.
La paternité de cette célèbre loi devrait être attribuée à Abraham de Moivre (1730) car, près d'un siècle plus tôt, ce dernier l'avait découverte en tant que loi approchée d'une distribution binomiale de moyenne m, d'écart type σ, lorsque le nombre d'expériences est grand.
Les astronomes Laplace et Gauss la construisirent qu'au tout début du 19è siècle, à la manière de de Moivre, dans le cadre de l'évaluation des erreurs commises sur des mesures d'observations (astronomiques en particulier) et il en sera de même de la célèbre méthode des moindres carrés conduisant à cette loi et également revendiquée tant par Laplace que Gauss et Legendre.
Méthode des moindres carrés : »
On dit souvent loi de Gauss, loi de Laplace-Gauss (appellation due à Fréchet) mais plus rarement loi de Laplace : expression plutôt réservée, au pluriel et comme vu plus haut, aux lois de l'électromagnétisme. On utilisera toujours ici la locution loi normale. Si une variable aléatoire T est soumise à une telle loi, on dira que T suit une loi normale.
Notion de variable aléatoire continue : »
On note généralement N(m,σ) la loi normale de moyenne m (espérance mathématique) et d'écart-type σ. Elle apparaît comme limite (convergence en loi) de la loi binomiale B(n,p) de même moyenne m = np et donc de même écart-type = np(1 - p). Sa densité est :

Rappel :
Centrer une variable aléatoire X, c'est faire le changement de variable X' = X - m où m désigne l'espérance mathématique de X; on a alors E(X') = 0.
Réduire une variable aléatoire X, c'est faire le changement de variable X'= X/σ
où σ désigne l'écart-type de X;
on a alors
σ(X') = 1.
Une variable centrée réduite s'obtient donc par la transformation affine X' = (X - m)/σ.
La densité de la loi normale N(0,1) centrée et réduite (parfois dite normée, m = 0, σ = 1) est alors :

Sa représentation graphique fournit la célèbre courbe en cloche, également dite cloche de Gauss. Sa fonction de répartition, généralement notée π (comme le célèbre nombre) est définie par :
![]()
Noter que l'on peut tout aussi bien écrire : π(t) = Prob(T ≤ t). La zone jaune ci-dessus représente π(0) = 0,5. La zone verte, pour t > 0, représente l'intégrale de f sur [o,t] . On a donc :
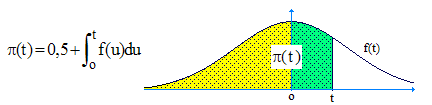
➔ Les tables fournissent généralement les probabilités pour 0 ≤ T ≤ 5 par pas de 0,1. à noter que π(4,5) = 0,9999... est déjà sensiblement égal à 1. Les propriétés élémentaires du calcul intégral et du calcul des probabilités permettent d'écrire (les inégalités peuvent être écrites au sens large) :
π(-t) = 1 - π(t) | Prob(a < T < b) = π(b) - π(a) | Prob(-a < T < a) = 2π(a) - 1
Des tables fournissant π(t) sont à la disposition des statisticiens. Outre le programme "maison" en ligne ci-dessous, utilisant la méthode de Poncelet, on pourra se référer à la table donnant t et π(t) sur le site de l'université de bordeaux ainsi qu'au site StatSoft (pour la loi de Gauss, il s'agit du signet Z Table).
! Si vous étudiez une variable aléatoire X soumise à (ou approchée par) une loi normale N(m,σ), vous devez pensez à réduire votre loi à la variable centrée réduite T afin d'utiliser correctement les tables :
X < a ⇔ T < (a - m)/σ ; a < X < b ⇔ (a - m)/σ < T < (b - m)/σ
Votre loi X est de moyenne 12, d'écart-type 3. Vous cherchez la probabilité de l'événement 8 < X < 15. Cela revient à calculer Prob(-4/3 < T < 1) = π(1) - π(-4/3) = π(1) + π(4/3) - 1 ≅ 0,75.

© Copyright
StatSoft, Inc., 1984-2005 -
z désigne ici notre t
Sur cet intervalle, le programme assure 4
décimales exactes et affiche l'erreur maximale
!
Prendre garde à entrer, par exemple,
2.7
(mode anglo-saxonne) et non pas
2,7 (à
la french) ! !
∗∗∗
La demande mensuelle X d'un produit, exprimée en
milliers d'unités, a évolué sur l'année écoulée
suivant le tableau ci-dessous :
| Mois | Janvier/Février | Mars/Avril | Mai/Juin | Juillet/Août | Septembre/Octobre | Novembre/Décembre |
| Demande | 100 | 128 | 178 | 150 | 140 | 126 |
En supposant que X suit une loi normale et que la demande restera sensiblement identique pour l'année en cours, calculer la probabilité pour que la demande mensuelle soit supérieure à 125 milliers d'unités.
Réponse : La moyenne est m =
Σxi
/6 = 137. La
variance, carré de l'écart-type
est Σ(xi -
m)2/6 = Σ(xi
- m)2/6 - m2 = 23,9..
≅ 24. La variable normale centrée
réduite de X est donc T = (X - 137)/24, soit X = 24T + 137 et on a :
Prob (X > 125)
⇔ 1 - Prob (X
≤ 125) = 1 -
Prob(T ≤ -0.5)
= 1 - π(-0.5) =
π(0.5) = 0,69
| Loi normale & loi binomiale : |
,
On a représenté ci-dessus les Prob{B = k} d'une loi binomiale B(6,½). On voit une répartition en cloche rappelant la loi normale : cette dernière apparaît effectivement en tant qu'approximation acceptable d'une loi binomiale lorsque n est "grand" avec p et q = 1 - p "non voisins" de 0 : n est grand et les probabilités de réalisation d'une éventualité et de son contraire sont comparables.
Les paramètres de la loi normale sont alors :
• la moyenne
(espérance mathématique) m = np;
• la variance
(carré de l'écart-type)
σ
Explication :
Pour une loi binomiale B(n,p), on a : Prob{B = k} = Cnk x pkqn-k et on sait que :

Une application (un peu compliquée...) de la formule de Stirling, permet de se débarrasser des factorielles au profit de l'exponentielle. On aboutit alors, en posant tk = (k - m)/σ (variable centrée réduite) à :
 (pk)
(pk)
C'est ainsi que Prob{B = k} est sensiblement égal (pour n "grand") à f(tk) où f désigne la densité gaussienne. C'est là une manifestation de la loi des grands nombres. Autrement dit :
Si n est suffisamment grand, la loi binomiale B(n,p) centrée réduite, à savoir :

suit sensiblement une loi normale centrée réduite.
Conditions d'usage :
Le
s conditions licites varient suivant les spécialistes... Généralement :n > 30 ou n > 50 avec npq >10;
ou bien np >15 et nq > 15.
Tout dépend du phénomène étudié et de la précision voulue. Par des raisons de symétrie de la courbe en cloche, l'approximation en question sera d'autant meilleure que si p et q seront "voisins", donc si p et q sont tous deux "proches" de 0,5. Un exemple d'application est donné dans le paragraphe suivant.
➔ Notons que la loi binomiale peut aussi être approchée par une loi de Poisson.
Théorème central limite : »
∗∗∗
Réponses : La variable normale centrée
réduite de N est T = (N - 1,95)/0,025. Donc N = 0,025T + 1,95.
1°/ Prob (N > 2)
⇔ Prob (0,025T
+ 1,95 > 2)
⇔ Prob(T
> 2)
= 1 - π(2) =
0,0228 = 22,8 o/oo (en pour mille). Le nombre (entier) cherché est
donc 23.
2°/ La situation s'interprète comme un tirage de 30 enveloppes dans une
population d'effectif 1000. Il s'agit d'une loi
binomiale B(n = 1000, p = 23/1000) que l'on peut approcher par la loi
normale de moyenne np = 23, d'écart-type σ = √(npq),
q = 1 - p, soit σ = 4,74. Prob (B ≤ 30) = Prob[T ≤ (30 - 23)/4,74]
≅ 0,93.
| Loi binomiale et trompeuse intuition... : |
Étudions cet exemple très simple d'utilisation de la loi normale afin d'approcher la loi binomiale :
Si l'on joue n fois (n pair) à pile ou face, par exemple 100 fois, quelle est la probabilité d'obtenir 50 "pile" ?
La réponse qui vient souvent à l'esprit est "0,5" ou "pas loin de 0,5"... Tout à fait faux : on doit ici appliquer la loi binomiale de paramètre n = 100 et p = 0,5. Si X est le nombre de "pile" obtenus :

Calcul des Cnp par l'ordinateur : »
On est à 8 chances sur 100, très loin de 50 sur 100 !!!
En l'absence d'ordinateur, calculer C10050 "à la main" ou 1/2100 n'est pas trivial et une calculatrice peut également ne pas apprécier de calculer 50! (factorielle 50) qui est de l'ordre de 3 × 1064. Mais il est ici légitime d'utiliser une approximation de la loi binomiale par la loi normale (» paragraphe précédent) :
La moyenne est ici m = np = 50. L'écart-type σ est :
![]()
et tk = (k - m)/σ
= 0 puisque k = 50. D'où, par usage de la formule (pk) : Prob{X = 50}
≅
 = 0,7978
≅ 0,08
= 0,7978
≅ 0,08
Conclusion :
Obtenir exactement 50 "pile" est effectivement "très" improbable sur 100 coups... En effet, vous conviendrez de la proximité des nombres mesurant les probabilités de X = 47 à X = 53 : ces valeurs varient symétriquement et sensiblement entre 0,07 et 0,08 (le maximum est obtenu en X = 50) : or 7 x 0,07 = 0,49. Pas loin de 0,5 : on a donc, grosso modo, 1 chance sur 2 d'obtenir un résultat entre 47 et 53. Plus n est grand, plus petites sont les chances d'obtenir autant de "pile" que de "face" !
Voyons cela en termes élémentaires :
Notons P l'événement "pile est sorti" et F l'événement contraire "face est sorti", on a :
si n = 2 : il nous faut 1 "pile". Il y a 22 = 4 éventualités : PP, PF, FF et FP équiprobables; deux sont favorables : PF ou FP; p = 2/4 = 1/2. On a un demi pile !.. En termes de loi binomiale :
p = C21 ×
(0,5)1 × (0,5)1 = 2 × 0,25 = 0,50si n = 4 : il nous faut 2 "pile". Il y a déjà là 24
= 16 éventualités. Procédons par ordre... :
- on peut obtenir 4 "pile" : PPPP, soit 1 cas;
- on peut obtenir 3 "pile" : PPPF, PPFP, PFPP, FPPP, soit 4
cas;
- on peut obtenir 2 "pile" : PPFF, PFPF, PFFP, FFPP, FPFP,
FPPF, soit 6 cas;
- on peut obtenir 1 "pile" : cas symétrique de 3
"pile" : FFFP, FFPF, FPFF, PFFF, soit 4 cas
- on peut obtenir 0 "pile" : FFFF, cas symétrique de 1
"pile", soit 1 cas
Sur ces 16 cas, 6 sont favorables : p = 6/16 = 3/8 = 0,375 : la probabilité diminue car le nombre de cas augmente et chacun veut sa part... En termes de loi binomiale : p = C42 x (0,5)2 x (0,5)2 = 6 x 0,625 = 0,375.
si n = 10, il y a 210 = 1024 cas et seulement 252 cas favorables (C105), soit une proba de 1/4 environ.
Combinatoire & calcul des Cnp : »
 ➔
Pour éviter des erreurs ou "oublis", on peut aussi procéder en construisant un
arbre des éventualités (à gauche) :
la
distribution des "pile" est conforme à la
courbe de Gauss.
Si X
désigne le nombre de faces obtenues, on a par exemple :
➔
Pour éviter des erreurs ou "oublis", on peut aussi procéder en construisant un
arbre des éventualités (à gauche) :
la
distribution des "pile" est conforme à la
courbe de Gauss.
Si X
désigne le nombre de faces obtenues, on a par exemple :
Prob (X = 1) = Prob (X = 99), Prob (X = 49) = Prob (X = 51), ...
car "pile" et "face" sont complémentaires et équiprobables (en supposant la pièce de monnaie parfaitement équilibrée...).
Et pour clore la discussion, ajoutons que la probabilité p = 0,5 est, selon la loi faible des grands nombres, une valeur fortement probable lorsque n devient très grand de la fréquence des "pile".
Effectivement : jouez à pile ou
face 100 fois, vos chances d'obtenir un nombre de "piles" proche de 50 sont fortes.
Proche de 50, pas
égal à 50... On parle de probabilité, donc de hasard, bien vu ? Sinon
revenez ici...
| Étude théorique : |
Soit X le nombre de "pile" obtenus. X suit une loi binomiale B(100, 1/2). On a vu ci-dessus que son espérance mathématique est 50 et son écart-type 5 : calculons alors la probabilité p d'obtenir entre 45 et 55 "pile". En termes de loi binomiale, cette probabilité s'écrit :
 (si le "entre" est au sens strict, on sommera de 46 à
54).
(si le "entre" est au sens strict, on sommera de 46 à
54).Le calcul de cette somme n'est pas simple. On obtient 0,632 (sens large) et 0,728 (sens strict). Mais le calcul par sommation est ici encore à éviter : on approxime par la loi normale :
et on lit sur la table de la loi normale centrée réduite :
Ce qui est conforme au calcul exact obtenu par la loi binomiale. Noter que la fourchette 40 < X < 60 est "beaucoup plus" probable, elle fournit p = 0,965.
| Équivalent pour n grand de la probabilité d'obtenir n piles et n faces en jouant 2n fois à pile ou face : |
Cette probabilité (d'obtenir n fois pile et n
fois face) sensiblement égale à
![]() . En effet, la valeur exacte est
donnée par la loi binomiale :
. En effet, la valeur exacte est
donnée par la loi binomiale :

Mais, selon la formule de Stirling, nous avons :
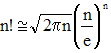
Ce qui fournit :

Ainsi, contrairement à l'opinion commune, plus vous jouez à pile ou face, moins vous avez de chances d'obtenir une probabilité proche de 0,5 pour vos n/2 "pile" : normal, dit la loi normale..., car vous augmentez le nombre d'éventualités, lesquelles ont chacune une petite chance de se réaliser.
| Estimation par intervalles de confiance : |
Étant donné un échantillon statistique {x1, x2, ..., xn} de taille n d'un caractère X (variable statistique ou aléatoire) étudié au sein d'une population relevant d'une loi binomiale, on cherche à estimer de façon fiable (à une certaine probabilité près mais proche de 1) la loi de probabilités suivie par X, tout particulièrement sa moyenne vraie (espérance mathématique m) et/ou sa fréquence vraie (proportion p) au sein de la population :
Estimation d'une moyenne (espérance mathématique) :
Les valeurs x1, x2, ..., xn de l'échantillon de taille n accompagnées de leurs fréquences respectives s'interprètent comme des variables aléatoires indépendantes X1, X2 , ..., Xn de même loi de probabilité que X. Soit alors m la moyenne vraie de X (espérance mathématique) et σ son écart-type. Posons Yn = ΣXi/n, moyenne des Xi. Dans ces conditions, E(Yn) = m (espérance) et V(Yn) = σ2/n (variance, carré de l'écart-type). Selon le théorème central-limite, lorsque n devient infini, la variable aléatoire centrée réduite de Yn, à savoir :

converge en loi vers la loi normale centrée réduite. C'est dire que :

En conséquence, en notant m' la moyenne observée de l'échantillon et σ' son écart-type. Il s'agit là de la probabilité pn, dit coefficient de confiance, que la moyenne vraie m de la loi de Gauss approchant la loi de l'échantillon appartienne à l'intervalle [m' - tσ'/√n, m' + tσ'/√n]. Dans la pratique, on se donne pn proche de 1 (par exemple 0,95 ≡ 95%) et on parle de calculer l'intervalle de confiance au risque de 1 - pn (0,05 ≡ 5%).
Estimation d'une proportion (probabilité, fréquence) :
On s'intéresse là à un caractère X suivant une loi binomiale B(n,p) dont on ne connaît pas la proportion au sein de la population étudiée. On ne connaît que la fréquence fn observée X/n d'un échantillon de taille n. On a (» Huygens) :
E(fn) = E(X)/n = np/n = p, V(fn) = V(X)/n2 = npq/n2 = pq/n (avec q = 1 - p)
On a vu que pour n "suffisamment" grand, la loi centrée réduite de B(n,p) définie par :

peut être assimilée à la loi normale (» loi normale et loi binomiale). Dans notre cas, on peut écrire :

et la variable aléatoire X1 peut s'interpréter en tant que fréquence centrée réduite. Notons alors pn la probabilité que X1 appartienne à l'intervalle [-t,+t]. On a :
 (f1)
(f1)
La dernière égalité peut aussi s'écrire :
 (f2)
(f2)
Or, pour n "grand", on a p ≅ fn et q = 1 - p = 1 - fn, (f2) fournit alors l'intervalle de confiance :

assurant au risque de 1 - pn, l'appartenance de la proportion vraie dans cet intervalle.
➔ Par exemple, l'intervalle de confiance au risque de 5%, couramment utilisé, conduit à 2π(t) - 1 = 1 - 5% = 0,95. On a donc π(t) = 0,975. La table de la loi normale centrée réduite (source univ. Bordeaux/univ. René Descartes) indique que t = 1,96 :

N.B. : au risque de 1%, on trouverait t = 2,58.
∗∗∗
Sur le site de l'APMEP
Sujet Bac S
juin 2014 Métropole Exercice 2
&
son corrigé
Sur le site Maths-France de
Jean-Louis Rouget :
Maths-France
Sujet Bac S
avril 2018 Pondichéry Exercice 3
&
son corrigé
Sujet Bac S
juin 2015 Centres étrangers Exercice 1 &
son corrigé
Sur ChronoMath :
Sujet BTS
services informatiques 1989