
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
 Dénombrer, c'est calculer le nombre exact
d'apparitions d'un phénomène, d'un événement ou la quantité (nombre entier)
d'objets clairement définis. Pascal s'est intéressé aux différentes façons de
combiner des objets distincts en tenant compte, ou pas, de l'ordre : étant
donnés n objets distincts on parle de
combinaisons et on note ici
Dénombrer, c'est calculer le nombre exact
d'apparitions d'un phénomène, d'un événement ou la quantité (nombre entier)
d'objets clairement définis. Pascal s'est intéressé aux différentes façons de
combiner des objets distincts en tenant compte, ou pas, de l'ordre : étant
donnés n objets distincts on parle de
combinaisons et on note ici ![]() ou C(n,p)
le nombre de façons de choisir p éléments parmi
ces objets (p = 0,1,...n), aucun ordre
n'intervenant dans ce choix. On dit aussi que
ou C(n,p)
le nombre de façons de choisir p éléments parmi
ces objets (p = 0,1,...n), aucun ordre
n'intervenant dans ce choix. On dit aussi que
![]() est le nombre de combinaisons de n objets pris p à p
ou plus simplement de combinaisons de p objets parmi n.
est le nombre de combinaisons de n objets pris p à p
ou plus simplement de combinaisons de p objets parmi n.
Parmi les 26 lettres de l'alphabet (n = 26), une combinaison de trois lettres (p = 3) peut être adk que l'on ne distinguera pas de kad, tout comme, en théorie des ensembles, {a,d,k} = {k,a,d}.
Si l'ordre intervient, distinction entre adk et kad, on parle d'arrangements que l'on peut identifier à des n-uplets : (a,d,k) ≠ (k,a,d). Et si p = n, on parle de permutation.
Dans le cas d'objets éventuellement identiques, on parle de combinaisons avec répétitions.
Combien peut-on former de mots de trois lettres ayant un sens ou non avec les lettres a, b, c (comme bac, aaa, aba, baa, cac, ...) ? La réponse est 10.
On peut aussi envisager des arrangements et des permutations avec répétition. Le dénombrement de ce type de problème est étudié en fin de page.
| Le triangle arithmétique : |
Les notations "à la française" :
![]() pour les combinaisons et
pour les combinaisons et
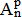 pour les arrangements apparaissent en 1904 dans
L'encyclopédie des sciences mathématiques pures et
appliquées publiée de 1904 à 1916 sous la direction de Jules Molk. Une autre notation
pour les combinaisons est également très utilisée :
pour les arrangements apparaissent en 1904 dans
L'encyclopédie des sciences mathématiques pures et
appliquées publiée de 1904 à 1916 sous la direction de Jules Molk. Une autre notation
pour les combinaisons est également très utilisée :

![]() ; on la doit
à
Euler qui
utilisa cette écriture en séparant n et p par un tiret, notation qui
perdura jusqu'au 19è siècle. Peu
pratique pour la rédaction, ChronoMath préfère utiliser Cnp
et Anp,
ou encore C(n,p) et A(n,p).
; on la doit
à
Euler qui
utilisa cette écriture en séparant n et p par un tiret, notation qui
perdura jusqu'au 19è siècle. Peu
pratique pour la rédaction, ChronoMath préfère utiliser Cnp
et Anp,
ou encore C(n,p) et A(n,p).
Nombre de parties d'un ensemble
:

La définition donnée en introduction montre que Cnp n'est autre que le nombre de parties de p éléments dans un ensemble de cardinal n (ayant n éléments). On en déduit accessoirement que le nombre de parties d'un ensemble (y compris lui-même : 1 cas correspondant à Cnn, et l'ensemble vide : 1 cas correspondant à Cn0) est :
Cn0 + Cn1 + Cn2 + ... Cnn-1 + Cnn = (1 + 1)n = 2n.
» Autre méthode de dénombrement » Exercice d'application
Le triangle arithmétique de Pascal est une table à double entrée dont l'algorithme de construction permet de calculer aisément les combinaisons Cnp et les coefficients du développement du binôme

en vertu de la formule de récurrence :

|
|
|
|
|
|
|
|
|
|
|
9 |
10 |
11 |
12 |
|
|
|
||||||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
9 |
1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | |||
|
10 |
1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 | ||
| 11 | 1 | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 1 | |
| 12 | 1 | 12 | 66 | 220 | 495 | 792 | 924 | 792 | 495 | 220 | 66 | 12 | 1 |
 Ce
"triangle arithmétique" était
cependant connu depuis fort longtemps car on en trouve l'usage dans l'algèbre d'Omar
al-Khayyam au 11è siècle ainsi que dans le Livre lumineux de l'arithmétique
d'As-Samaw'al (1125?-1175) qui écrivait le tenir d'Al-Karaji (970?-1020).
Plus
tard, Al-Kashi le
décrira dans sa Clé de l'arithmétique (1427). L'arithmétique chinoise
n'est pas en reste : le fameux triangle apparaît au au tout début du 14è
siècle dans Le précieux miroir des
quatre éléments
du mathématicien Chu Shih-Chieh en tant que compilation de résultats
antérieurs, sans doute du 11è siècle,
donc à l'époque à d'Omar
al-Khayyam. Croisement des connaissances entre les civilisations chinoise et
des Arabes d'orient ?
Ce
"triangle arithmétique" était
cependant connu depuis fort longtemps car on en trouve l'usage dans l'algèbre d'Omar
al-Khayyam au 11è siècle ainsi que dans le Livre lumineux de l'arithmétique
d'As-Samaw'al (1125?-1175) qui écrivait le tenir d'Al-Karaji (970?-1020).
Plus
tard, Al-Kashi le
décrira dans sa Clé de l'arithmétique (1427). L'arithmétique chinoise
n'est pas en reste : le fameux triangle apparaît au au tout début du 14è
siècle dans Le précieux miroir des
quatre éléments
du mathématicien Chu Shih-Chieh en tant que compilation de résultats
antérieurs, sans doute du 11è siècle,
donc à l'époque à d'Omar
al-Khayyam. Croisement des connaissances entre les civilisations chinoise et
des Arabes d'orient ?
∗∗∗
a) Justifier sans utiliser le triangle de Pascal que Cn2 =
n(n - 1)/2 et que Cnn-1 = Cn1 = n.
b)
On vous distribue 5 cartes d'un jeu de 32 sans jokers. Combien y a-t-il de
possibilités de recevoir exactement 3 rois ?
Rép. a) choisir 2 cartes parmi n, c'est choisir une première carte c1 parmi n puis une seconde carte c2 parmi n - 1, conduisant à n × (n - 1) possibilités; mais en termes de combinaisons, les choix c1 puis c2 et c2 puis c1 ne font qu'un. La réponse est donc Cn2 = n(n - 1)/2. Par ailleurs, choisir n - 1 cartes parmi n, revient à choisir une carte parmi les n que l'on met de côté. Donc Cnn-1 = Cn1 et il y a n façons de faire ainsi.
Rép. b) Il faut en main 3 rois parmi 4, soit C43 = C41 = 4 cas et 2 autres cartes choisies parmi 28, soit C282 = 378 cas. Il y a donc C43 × C282 = 1512 possibilités d'avoir en main un "brelan" de rois (aux cartes, une paire, un brelan, un carré =resp. 2, 3, 4 cartes de même valeur).
∗∗∗
Vérifier les formules : (n - p) × Cnp
= (p + 1) × Cnp+1
et n × Cn-1p-1
= p × Cnp
Cnp+1 = Cpp + Cp+1p
+ Cp+2p + ... + Cn-1p
Explication et usage, programmation sur tableur : » Calcul des combinaisons (JavaScript) : »
| Dénombrement des arrangements, permutations et combinaisons ainsi que des applications, injections et bijections : |
Voici l'arbre d'un choix ordonné de 3 objets parmi 4. On parle d'arrangement de 3 objets parmi 4. Par ordonné, on veut signifier par exemple que :
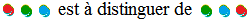
➔
Un arrangement de p éléments est assimilable à un p-uplet (a1, a2, ..., ap). Une combinaison est assimilable à un ensemble {a1, a2, ..., ap}.Au départ, on a le choix sur 4 éléments;
Au second choix, pour chacun de ces 4 éléments, on
peut associer 3 possibilités;
d'où déjà 4 × 3
= 12 cas.
Il reste alors 2 choix possibles associés à chacun de ces cas. Il y a finalement 12 × 2 = 24 possibilités :

A
On déduit facilement de cet exemple (principe de la multiplication) que le nombre d'arrangements distincts de p objets parmi n est donné par le nombre noté Anp
tel que Ano = 1 (convention) et, pour p non nul :Anp = n(n - 1)(n - 2)(...)(n - p + 1).
➔ Remarquer que Ann = n! (factorielle n) : lorsque n = p, on parle de permutations de n objets distincts. Rappelons que la notation n!, factorielle de n, est le nombre 1 × 2 × 3 ×... × n.
Christian Kramp et la notion de factorielle : » » Stirling
∗∗∗ Un exercice de dénombrement niveau 3ème/2nde , Dénombrement et probabilités (Bac S/ES)
à chaque arrangement de p éléments correspond p! façons (factorielle p) de changer l'ordre. Par suite :
Cnp = Anp/p!
![]()
Lien avec le nombre d'injection et de bijections :
Le nombre Anp est le nombre d'injections d'un ensemble Ep vers un ensemble Fn (p ≤ n). Lorsque p = n, il s'agira donc du nombre de bijections de En vers un ensemble Fn. Il y a donc Ann = n! bijections.
Injections, surjections, bijections : » Nombre de surjections : »
Nombre d'applications :
➔ Rappelons aussi que l'on peut définir np applications d'un ensemble Ep de cardinal p vers un ensemble Fn de cardinal n (attention à l'ordre). En effet, une telle application s'identifie à un n-uplet (im1, im2, ..., imp), les images imk étant choisies parmi n (deux éléments de Ep peuvent avoir ici la même image contrairement à l'injection), d'où l'existence de n × n × ... × n = np cas possibles (p facteurs).
Arrangement avec répétition : »
∗∗∗
| Programme JavaScript calculant combinaisons et arrangements : |
➔ Le programme est très simple. Les fonctions comb() et fac() sont identiques à celles présentes dans le calcul des combinaisons à la page Blaise Pascal.
! Au-delà de 16 chiffres significatifs, on dépasse la capacité de traitement en nombres entiers du langage JavaScript. Les résultats n'on alors plus guère de sens, sinon un ordre de grandeur.
<SCRIPT LANGUAGE=JavaScript>
function go()
{
var nn,n,k
nn="";;k="";
ok=1;
while (ok=1)
{
nn=eval(prompt("Entrez n :",nn))
if(nn==null) return
k=eval(prompt("Entrez p :",k))
if(k==null){ok=0}
if(k<nn-k) {c=comb(nn,k)} else {c=comb(nn,nn-k)}
a=c*fac(k)
if(ok==1){alert("A("+nn+","+k+") = "+a+" , C("+nn+","+k+") = "+c)};
if(!confirm("Autre calcul ?")) return
}
}
function fac(n)
{
if (n<=1){return 1};
f=1;
for(i=2;i<=n;i++){f=f*i}
return f
}
function comb(n,p)
{
if (n==p || p==0){return 1};
if (p==1){return n};
num=n;
for(i=1;i<=p-1;i++){num=num*(n-i)}
return num/fac(p)
}
</SCRIPT>
| Arrangements, permutations et combinaisons avec répétition : |
a/ Arrangement avec répétition :
Un arrangement avec répétition de p éléments parmi n objets distincts a1, a2, ..., an consiste en un choix ordonné de p objets choisis parmi les n en tenant compte de l'ordre de ces éléments : c'est un p-uplet (ai1, ai2, ..., aip)
Un arrangement avec répétition s'identifie donc une application d'un ensemble Ep de cardinal p vers un ensemble Fn de cardinal n. En notant Ãnp leur nombre (Ã= "A tilda"), on a donc :
Ãnp = np
Combien peut-on écrire de mots de 3 lettres (p = 3) ayant ou non un sens avec les 26 lettres de l'alphabet (n = 26) ? Il s'agit d'arranger 3 lettres parmi 26 avec la possibilité de répéter les lettres. La réponse est donc 263 = 17576 cas allant de aaa, aab, ... jusqu'à zzz.
b/ Permutation avec répétition :
Une permutation avec répétition de n éléments consiste en un rangement de n objets (n-uplet) distincts ou non sachant qu'il n'y a que k objets distincts parmi les n. Notons p1, p2, ..., pk les nombres de répétition des objets 1, 2, ..., k dans la collection. On a p1 + p2 + ... + pk = n. Si tous les objets étaient distincts, nous aurions n! permutations distinctes. Les permutations des objets 1, 2, ..., k laissent invariante une permutation donnée, le nombre total de permutations avec répétition est donc (» factorielle) :
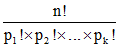
• Combien y a-t-il de "mots" distincts, n'ayant pas nécessairement de sens, obtenus à partir du mot pape, ? Il y a 4 lettres, dont 2 "p". Le dénominateur de notre formule est 2! × 1! × 1! = 2. On a donc 4!/2 mots, soit 12 : Vérifions cela : commençant par p, on a ppae, ppea, paep, pape, pepa, peap (3! = 6 cas); commençant par a, on a aepp, apep, appe (3!/2! = 3 cas), de même si on commence par e : on a bien en tout 6 + 3 + 3 = 12 cas.
• Combien y a-t-il de "mots" distincts, n'ayant pas nécessairement de sens, obtenus à partir du mot abracadabra ? Il y a 11 lettres, dont 5 "a", 2 "b", 2 "r", 1 "c" et 1 "d". Le dénominateur de notre formule est 5! × 2! × 2! × 1! × 1! = 480. On a donc 11!/480 mots, soit 83160. Faisant confiance à la formule, nous ne ferons pas la liste de tous ces cas...
c/ Combinaison avec répétition :
Une combinaison avec répétition de p éléments parmi n objets distincts consiste en un choix de p objets distincts ou non parmi les n en ne tenant pas compte de l'ordre des éléments choisis. Le dénombrement de ces combinaisons est un peu plus difficile à évaluer. Leur notation n'est pas normalisée, on rencontre un peu de tout. On utilisera ici Č(n,p).
• Première formule de récurrence :
Comme pour les combinaisons "ordinaires", on peut donner sans difficulté une première formule de récurrence : parmi les combinaisons avec répétition contenant un élément a, notons A (resp. B) l'ensemble des combinaisons qui contiennent (resp. ne contiennent pas) a. On a Č(n,p) = Card A + Card B.
Dans l'ensemble A, retirons une seule fois a à chacune des combinaisons : on a Č(n,p-1) combinaisons de cette sorte, et c'est le cardinal de A. L'ensemble B est constitué des combinaison avec répétition ne contenant pas a : on en a Č(n-1,p) et c'est le cardinal de B. Finalement, ce raisonnement, qui sous-entend n ≥ 2 et 2 ≤ p ≤ n-1, fournit :
Č(n,p) = Č(n,p-1) + Č(n-1,p) (r)
On peut donner un sens aux cas particuliers permettant le bon "fonctionnement" de cette relation de récurrence :
n non nul, p = 1 : combinaison avec répétition de n éléments pris 1 à 1 : Č(n,1) = n;
Finalement, on peut écrire :
Č(n,p) = Č(n,p-1) + Č(n-1,p) , n ≥ 2, 0 ≤ p ≤ n-1
! n = p ne peut convenir à cause de la présence de Č(n-1,p). C'est dire que le calcul de Č(n,n) pose problème mais il y a une solution étudiée plus loin...
Quelques cas particuliers :
Č(2,2) : la formule
ne convient pas ici car nous aurions à calculer Č(1,2), donc p > n !
Faisons un calcul direct.
Nous avons deux éléments a et b à combiner 2 à 2
avec répétition : on obtient aa, bb, ab. Donc Č(2,2) = 3.
Č(n,2) = Č(n,1) + Č(n-1,2)
Č(n-1,2) = Č(n-1,1) + Č(n-2,2)
Č(n-2,2) = Č(n-2,1) + Č(n-3,2)
...
Č(3,2) = Č(3,1) + Č(2,2)Faisons la somme membre à membre : Č(n,2) = Č(n,1) + Č(n-1,1) + Č(n-2,1) + ... + Č(3,1) + Č(2,2) = n + (n-1) + (n-2) + ... + 3 + 3. Mais 3 = 2 + 1. On voit donc que :
Č(n,2) = n(n + 1)/2 est la somme des n premiers entiers naturels (non nuls)
• Seconde formule de récurrence et calcul direct :
Vu les difficultés du calcul par récurrence des Č(n,p), on aimerait avoir une formule simple et directe ! La voici : chaque combinaison avec répétition contient p éléments distincts ou non, donc lorsqu'on écrit toutes les combinaisons, on écrit en tout pČ(n,p) éléments où chacun d'eux jouent le même rôle. C'est dire que si on se fixe un élément a comme nous l'avons fait dans la recherche de la formule de récurrence, celui-ci est utilisé pČ(n,p)/n fois.
Supposons avoir ordonné chaque combinaison avec répétition en commençant par a et, comme précédemment, nous allons supprimer une seule fois a en début d'écriture en illustrant le raisonnement avec le cas de 4 éléments a, b, c, d pris 3 à 3. Nous avons dans ce cas 20 combinaisons à répétions que l'on peut ordonner ainsi :
aaa, aab, aac, aad, abb, abc, abd, acc, acd, add || bbb, bbc, bbd, bcc, bcd, bdd || ccc, ccd, cdd || ddd
La partie bleue ne contient pas de a (on les a épuisés dans la partie rouge), négligeons-la :
aaa, aab, aac, aad, abb, abc, abd, acc, acd, add (1)
Selon le résultat précédent, on a écrit 3Č(4,3)/4 = 15 fois la lettre a, ce que l'on vérifie facilement. Plus généralement on en aurait pČ(n,p)/n.
Mettons maintenant le premier a à part :
aa , ab , ac , ad , bb , bc , bd , cc , cd , dc , dd (2)
la liste de la ligne (2) représente les combinaisons à répétition de 4 éléments pris 2 à 2 au nombre de Č(4,2), plus généralement Č(n,p-1) et cette ligne contient donc 2Č(4,2)/4 = 4(4+1)/4 = 5 fois la lettre a, ce que l'on vérifie. Plus généralement, on en aurait (p-1)Č(n,p-1)/n.
Pour dénombrer tous les a, il nous faut maintenant ajouter ceux que l'on a retirés ! : il y en a autant que de combinaisons dans la ligne 2, soit Č(4,2) et plus généralement Č(n,p-1) comme déjà dit. Finalement, nous obtenons une formule de récurrence plus opérationnelle que la précédente car seul p est affecté :
pČ(n,p)/n = (p-1)Č(n,p-1)/n + Č(n,p-1)
Ce qui s'écrit plus simplement :
pČ(n,p) = (n + p - 1)Č(n,p-1) , n ≥ 1, 1 ≤ p ≤ n
Faisons décroître p par pas de 1 :
pČ(n,p) = (n + p - 1)Č(n,p-1)
(p-1)Č(n,p-1) = (n + p - 2)Č(n,p-2)
(p-2)Č(n,p-2) = (n + p - 3)Č(n,p-3)
...
3Č(n,3) = (n + 2)Č(n,2)
2Č(n,2) = (n + 1)Č(n,1)
Multiplions membre à membre et simplifions : p!Č(n,p) = (n + 1)(n + 2)...(n + p - 1)Č(n,1). On a vu que Č(n,1) = n. Donc, en divisant par p! et sachant que :
![]()
On en déduit la formule, fort simple :
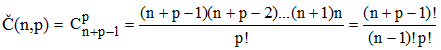
Nous voulions précédemment calculer Č(n,n) et avons reculé devant la difficulté ! Cela ne pose désormais plus de problème :
➔
Pour en savoir plus :i Jules Molk : mathématicien français (1857-1914); après des études secondaires à Strasbourg (sa ville natale) et à Mulhouse, Jules Molk entre à l'École polytechnique fédérale de Zürich (ETH) ou Frobenius fut un de ses professeurs. A l'issue de son cursus, il se rend à Paris puis à Berlin où il rencontre et suit les cours de professeurs de renommée internationale (Hermite, Bouquet, Tannery, Weierstrass, Kronecker, ...) et soutiendra une thèse de doctorat auprès de ce dernier à l'université de Berlin (Sur une notion qui comprend celle de la divisibilité et sur la théorie générale de l'élimination, 1884, » ici...). En 1890, il succède à Émile Mathieu à l'université de Nancy et s'oriente vers l'analyse avec l'étude approfondie des fonctions et intégrales elliptiques. Source : Hommage à Jules Molk rédigé par son collègue et ami Henri Vogt (1864-1927), professeur à Nancy (Éd. Jacques Gabay).
Le triangle arithmétique à travers les âges, par
Michel Guillemot (univ. Toulouse), Bulletin APMEP n°416, 1997 :
https://www.apmep.fr/IMG/pdf/AAA98031.pdf
Dénombrement et (équi)-probabilité, exercices corrigés,
par Mathieu Sablik, univ. de Toulouse/IUT Aix en Provence, 2012 :
https://www.math.univ-toulouse.fr/~msablik/CoursIUT/Proba/2012-2013-Proba-TD3-Denombrement.pdf