
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
On sait que si une courbe est définie en coordonnées paramétriques par une relation de la forme x = f(t), y = g(t), la longueur d'un arc AB est donnée par :
![]()
Considérons une ellipse d'équation réduite (a > b) :
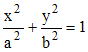

Comme écrit à la page intégrales elliptiques, on peut paramétrer par : x = a.sint et y = b.cost et le calcul de la longueur d'arc BA d'un quart d'ellipse conduit au calcul de l'intégrale :

e < 1 désignant l'excentricité de l'ellipse.
Cette intégrale elliptique n'est pas calculable par quadrature. Mais e2sin2u < 1 permet un développement en série du radical :
![]()
ce qui conduit à :
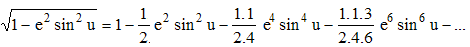
et cette série converge uniformément. On peut donc intégrer terme à terme. Pour ce faire, il nous faut connaître l'intégrale de Wallis :

et le résultat pour n pair que l'on peut mettre sous la forme

Grâce à ce développement, nous allons alors calculer :

correspondant à une demi-ellipse :

Le 1er terme fournira π que nous mettons en facteur en remplaçant chaque intégrale de sinus par sa valeur correspondante I2n. La circonférence de l'ellipse est donc, en usant d'une petite astuce permettant une formule plus "esthétique" :
