ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

On se propose de calculer l'intégrale généralisée ci-dessous, dite de Gauss :

 

Désignons par D le quart de plan défini par x ≥ 0, y ≥ 0 et considérons l'intégrale double :

dont nous admettons l'existence. Selon le théorème de Fubini, on peut écrire :

En application du changement de variables dans une intégrale double et de la notion de jacobien, on peut passer en coordonnées polaires en posant x = r.cost et y = r.sint avec r positif et t élément de [0,π/2]. Dans ce cas, le jacobien est celui de la fonction (r, t) → (r.cost, r.sint), soit :

Vu que cos²t + sin²t = 1, on a x² + y² = r² et l'intégrale double devient :

où K est le domaine équivalent à D en coordonnées polaires, donc défini par r positif et t élément de [0,π/2]. Ainsi :

d'où :

et par suite, l'intégrale de Gauss, vaut :

 ➔   Suivant les auteurs, l'intégrale de Gauss présente quelques variantes :

• Si l'on intègre e^-x²/2 sur R tout entier, alors, par parité, on trouve un résultat double : G = √(2π).
• Si l'on intègre e^-x² sur R⁺, en posant x = u√2, on vérifie facilement que G prend la valeur √π/2.
• Enfin, si c'est l'intégrale sur R tout entier de e^-x² que l'on considère, alors G = √π.

Considérons la transformée de Fourier F de la fonction x → f(x) = exp(-x²/2) :

f étant paire, on a :

     (1)

Dérivons formellement sous le signe somme par rapport à ω en écrivant :

Pour tout t, on a :

Le membre de droite de cette inégalité est une fonction positive et intégrable sur R⁺ : c'est la dérivée de -exp(-t²/2), son intégrale est égale à 1. Par suite, en appliquant le théorème de dérivation sous le signe somme pour les intégrales généralisées, on peut affirmer que F'(ω) désigne la dérivée de F(ω).

♦  Calculer alors F'(ω) par intégration par parties. Facile ! Vous devriez trouver : F'(ω) = - xF(ω).

♦  Voilà un beau résultat qui nous conduit tout simplement comme tout bon lycéen de Terminale S à :

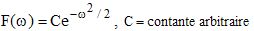
♦  Notre fonction f est continue, utilisons la formule d'inversion :

    En remplaçant F(ω) par la valeur trouvée et en changeant ω en -ω, on vérifie que :

♦ On en déduit la valeur de C puis la transformée de Fourier de la fonction  x → exp(-x²/2) à savoir :

ω → 1/√(2π) × exp(-ω²/2)

C'est dire qu'à un coefficient multiplicatif près, la transformée de Fourier de la loi normale est identique à elle-même. C'est la seule fonction possédant cette propriété remarquable.

♦  En faisant x = 0, dans la formule (1), on conclut :

 ➔   Rappelons encore ici, que suivant les auteurs :

• Si l'on intègre e^-x²/2 sur R tout entier, alors, par parité, on trouve un résultat double : G = √(2π).
• Si l'on intègre e^-x² sur R⁺, en posant x = u√2, on vérifie facilement que G prend la valeur √π/2.
• Enfin, si c'est l'intégrale sur R tout entier de e^-x² que l'on considère, alors G = √π .