ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Transformation de Fourier            
 » Transformée de Laplace , produit de convolution au sens de Fourier , au sens de Laplace

Soit f est une fonction définie sur R et à valeurs dans R ou C, la transformée de Fourier de f est la fonction définie par :

L'existence de F est assurée lorsque f est absolument intégrable sur R, c'est à dire lorsque ∫R |f(t)| dt est convergente  (» espaces Lp)

 !  Cette fonction est souvent notée f circonflexe, nous la noterons ici F ou parfois ^f. Suivant les auteurs, les objectifs et les changements de variables, la transformée de Fourier admet plusieurs définitions susceptibles de changer certains résultats à des constantes multiplicatives près. Par exemple, pour mieux concorder avec le calcul des probabilités (fonction caractéristique d'une variable aléatoire), le coefficient 1/2π peut être absent et iωt remplace -iωt.

La transformation de Fourier apparaît dans de nombreux phénomènes physiques (électricité, équations des cordes ou des membranes vibrantes, équation de la chaleur, théorie du signal, ...). On utilise d'ailleurs ici la variable ω (pulsation) car lorsque f correspond à la description d'un signal à l'instant t, sa transformée F s'interprète comme la description de sa fréquence ω/2π (voir ci-après).

Formule d'inversion, également appelées formule de réciprocité :

Si f est au moins de classe C1 par morceaux, alors pour tout réel x, on a la formule de inversion (ou de réciprocité) de la transformation de Fourier :

 ➔   Cas d'une intégrale généralisée : 

Lorsque f est continue et F intégrable sur R, on trouve la formule d'inversion affirmée par Fourier sans trop de précautions... :

            »  Plancherel         

Comme dit ci-dessus, si F(ω) est définie par l'intégrale sur R de f(t)eiωt, alors, par inversion, le coefficient 1/2π réapparaît et -iωx remplace iωx.

Théorème d'inversion dans un cas élémentaire et pratique (mais pas évident à démontrer...) :

On suppose f positive, non croissante sur l'intervalle [0,+∞[, de limite nulle en +∞. Si f est intégrable sur tout intervalle [0,α], α > 0, alors, en posant :

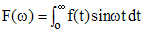
On a :


f(x+0) et f(x-0) désignent les limites respectives à droite et à gauche de f au point x.

 ∗∗∗ Application :  calcul de l'intégrale de Gauss , calcul des intégrales de Fresnel

Interprétation de la transformé de Fourier, spectre, densité spectrale :

Avec la notation complexe (usage des coefficients exponentiels ), la série de Fourier de f peut s'écrire :     

                » Espace L2 et série de Fourier

Le produit nω est la pulsation de l'harmonique de rang n. Lorsque la fonction f est obtenue par échantillonnage (cas statistique d'un "nuage" de points), en superposant des harmoniques d'amplitudes ck et de pulsations ωk (fréquences νk = ωk/2π) diverses, cette série prend la forme approchée :

En discrétisant l'intervalle d'intégration à la manière de Riemann, la formule d'inversion (inv) s'interprète comme la limite de sommes de la forme

ΣF(ωk)eiωkxΔωk

et en comparant à la formule ci-dessus exprimant f(x), le produit F(ωk)Δωk apparaît être une variation d'amplitude Δck = F(ωk)Δωk.

Revenant au cas continu, en notant ω → A(ω) l'amplitude, fonction de ω, peut écrire dA= F(ω)dω ou dA/dω = F(ω) : la transformée de Fourier apparaît comme une densité d'amplitude : à l'image d'une distribution de probabilités, l'amplitude décrit une distribution de fréquences.

Pour ces raisons, on appelle spectre de fréquence la représentation en bâtons (on parle plutôt de raies) νn → cn de l'amplitude cn de chaque harmonique en fonction de sa fréquence νn, ou ce qui est équivalent, n → cn, puisque la fréquence νn = nω/2π est proportionnelle à n (et ω). Avec ce vocabulaire, la transformée de Fourier est aussi qualifiée de densité spectrale.

» Si la série est donnée au moyen des coefficients exponentiels, le spectre est donné par n → |cn|. Le mot spectre est dérivé du latin spectare = regarder, contempler (qui a donné spectacle) et de spectrum = vision, fantôme. Le terme a été utilisé pour la 1ère fois par Newton au sujet de la décomposition de la lumière blanche (raies de lumière) par un prisme : vision de toutes les couleurs.  D'une façon générale le spectre d'un signal est l'analyse de ce dernier par l'étude de ses fréquences ou ses longueurs d'onde.

 ➔   Lorsque la fonction f n'est connue qu'en un certain nombre n de points (échantillonnage), on est amené, sans chercher une courbe de régression, à la transformée de Fourier discrète dont les américains Tukey et Cooley ont donné à des fins militaires (1965), un algorithme de calcul rapide : la FFT, Fast Fourier Transform évaluant f par inversion.

En savoir plus sur la transformée de Fourier discrète : »

Produit de convolution :

 Lorsque le produit t → f(x - t)g(t) est intégrable sur R, le produit de convolution de f et g est :

(f ∗ g)(x) = ∫R f(x - t)g(t)dt

En notant ici ^f  la transformée de Fourier d'une fonction f, on a ces résultats remarquables relatives au produit de convolution :

^(f ∗ g) = ^f × ^g   et   ^(f × g) = ^f ∗^g
 

»  Plancherel                 Transformée de Laplace : »          

∗∗∗ 
a)  Intégrale de Gauss et transformée de Fourier
b)  Exercices avec solutions : Université Joseph Fourier (Grenoble) , fichier pdf

 ➔  Pour en savoir plus :

Argand  Français
© Serge Mehl - www.chronomath.com